1. 核心要素与马尔可夫决策过程 (MDP)

强化学习 (Reinforcement Learning, RL) 的问题通常被数学化地建模为马尔可夫决策过程 (Markov Decision Process, MDP)。一个 MDP 由一个五元组 $(\mathcal{S},\mathcal{A},P,R,\gamma )$ 定义，它描述了智能体与环境交互的完整框架。

1.1. 智能体 (Agent) 与环境 (Environment)

• 智能体 (Agent): 学习者和决策者。它通过感知环境状态并选择行动来与环境交互。例如，玩游戏的 AI，自动驾驶的汽车，下棋的程序。
• 环境 (Environment): 智能体所处的外部世界，它接收智能体的行动，并以新状态和奖励作为响应。例如，游戏本身，真实的道路，棋盘。

交互循环过程:

1. 在时间步 $t$，智能体观察到环境的状态 $S_t=s$。
2. 智能体根据其策略 $\pi$ 选择一个行动 $A_t=a$。
3. 环境接收行动 $a$，发生状态转移，进入新的状态 $S_{t+1}=s^{\prime }$。
4. 环境向智能体反馈一个即时奖励 $R_{t+1}=r$。
5. 智能体进入新状态 $s^{\prime }$，循环继续。
   

1.2. MDP 的核心组成部分

状态 (State, $s\in \mathcal{S}$)

• 状态空间 (State Space) $\mathcal{S}$: 环境所有可能状态的集合。
• 状态 (State): 对环境在某一时刻的完整描述。一个好的状态必须具备马尔可夫性质（见 1.3 节）。
• 例子: 在棋类游戏中，状态是棋盘上所有棋子的位置；在机器人导航中，状态可以是机器人的坐标和速度。

行动 (Action, $a\in \mathcal{A}(s)$)

• 行动空间 (Action Space) $\mathcal{A}(s)$: 在状态 $s$ 下，智能体可以采取的所有可能行动的集合。
• 行动 (Action): 智能体可以做出的决策。
• 例子: 在棋类游戏中，行动是在某个位置落子；在机器人导航中，行动是“向前”、“向左转”、“向右转”。

环境动态 (Environment Dynamics): 转移与奖励

环境的动态描述了它如何根据智能体的行动而改变，这由状态转移和奖励两部分共同定义。

• 状态转移概率 (State Transition Probability, $P$):

  • $P(s^{\prime }|s,a)=\mathbb{P}[S_{t+1}=s^{\prime }|S_t=s,A_t=a]$
  • 它表示在状态 $s$ 采取行动 $a$ 后，环境转移到下一个状态 $s^{\prime }$ 的概率。
  • 确定性环境: 如果 $P(s^{\prime }|s,a)$ 对某个 $s^{\prime }$ 恒为 1，则环境是确定的。
  • 随机性环境: 如果 $P(s^{\prime }|s,a)$ 是一个概率分布，则环境是随机的（如掷骰子）。

• 奖励 (Reward, $r\in \mathcal{R}$):

  • 奖励是 RL 的核心驱动力，是你为智能体设定的目标，可以被视为一种人机交互接口 (Human-Machine Interface)。
  • 在最通用的形式下，奖励由一个奖励概率分布描述：$p(r|s,a)=\mathbb{P}[R_{t+1}=r|S_t=s,A_t=a]$。
  • 更常见地，我们使用奖励函数 (Reward Function)，它代表期望奖励。根据定义的不同，它可以是：
    • $R(s,a)=\mathbb{E}[R_{t+1}|S_t=s,A_t=a]$ (奖励只与当前状态和行动有关)
    • $R(s,a,s^{\prime })=\mathbb{E}[R_{t+1}|S_t=s,A_t=a,S_{t+1}=s^{\prime }]$ (奖励与完整的状态转移有关)
  • 目标: 智能体的目标不是最大化单步的即时奖励，而是最大化未来的累积奖励。

策略 (Policy, $\pi$)

• 策略是智能体的“大脑”或“行为准则”，它定义了智能体在特定状态下如何选择行动。
  • $\pi (a|s)=\mathbb{P}[A_t=a|S_t=s]$
• 确定性策略 (Deterministic Policy): $\pi (s)=a$。在每个状态下，选择唯一的行动。
• 随机性策略 (Stochastic Policy): $\pi (a|s)$ 是一个概率分布，在状态 $s$ 下以一定概率选择行动 $a$。
• 强化学习的目标就是找到一个最优策略 ${\pi }^{\ast }$，使得累积奖励最大化。

最优策略与最优价值函数

• 由于对称性等情况，可能存在多个不同的最优策略。
• 但是，对于一个给定的 MDP，最优价值函数 $V^{\ast }(s)$ 和最优行动价值函数 $Q^{\ast }(s,a)$ 是唯一的。这意味着能达到的最好结果是唯一的，但达到该结果的方法（策略）可以不唯一。

折扣因子 (Discount Factor, $\gamma$)

• $\gamma \in [0,1]$ 是一个用于衡量未来奖励重要性的超参数。它将未来的奖励进行折现，使得回报（Return）的总和是一个有限值。
  • $G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\dots$
  • $\gamma \to 0$ 使智能体“短视”，$\gamma \to 1$ 使智能体“有远见”。

1.3. 马尔可夫性质 (The Markov Property)

马尔可夫性质是 MDP 的基石，也被称为**“无记忆性” (Memoryless Property)**。

• 直观理解: 未来只与当前有关，而与过去无关。如果知道了系统当前的状态 $S_t$，那么所有之前的历史信息对于预测未来都不再提供任何额外的信息。

• 数学定义: 一个状态 $S_t$ 是马尔可夫的，当且仅当：

  • $p(s_{t+1}|s_t,a_t)=p(s_{t+1}|s_t,a_t,s_{t-1},a_{t-1},\dots ,s_0,a_0)$
  • $p(r_{t+1}|s_t,a_t)=p(r_{t+1}|s_t,a_t,s_{t-1},a_{t-1},\dots ,s_0,a_0)$

• 重要性: 它极大地简化了问题模型，使得我们可以仅根据当前状态来定义价值函数和制定决策。

2. 交互的实践: 轨迹与任务类型

2.1. 轨迹 (Trajectory) / 经验 (Experience)

轨迹 (也称 Episode, Rollout) 是智能体与环境进行一系列连续交互后产生的序列记录。它是所有学习算法赖以运行的数据基础。

• 定义: 一条轨迹 $\tau$ 是由状态、行动、奖励组成的序列：$$\tau =(S_0,A_0,R_1,S_1,A_1,R_2,S_2,\dots )$$

2.2. 任务类型与统一框架

• 分幕式任务 (Episodic Tasks): 任务有明确的终点（终止状态, Terminal State）。例如，一局棋、一轮游戏。
• 连续性任务 (Continuing Tasks): 任务没有终点，会无限进行下去。例如，机器人维持平衡。

处理目标状态的两种哲学 (Option 1 vs. Option 2)

我们可以通过不同的建模方式来处理任务的“目标”或“终点”。

• Option 1: 吸收状态 (Absorbing State):

  • 做法: 将所有终止状态转换为一个特殊的吸收状态。一旦进入，智能体将永远无法离开，且后续所有奖励均为零。
  • 效果: 这是一种将分幕式任务在数学上统一为连续性任务的技巧。无限回报公式 $G_t=\sum {\gamma }^k{R}_{t+k+1}$ 会在进入吸收状态后自然截断，极大地简化了理论和算法设计。

• Option 2: 普通奖励状态 (Normal Rewarding State):

  • 做法: 将目标状态视为一个普通的、可重复访问的状态。智能体在每次进入该状态时获得奖励，但任务不结束，它必须选择行动离开。
  • 效果: 这定义了一个纯粹的连续性任务，目标通常是最大化长期平均回报率。这适用于需要持续运行和优化的任务，如资源管理或机器人巡航。

2.3. 轨迹在学习中的作用

轨迹是智能体学习的原材料。不同算法利用轨迹的方式不同：

• 蒙特卡洛 (MC) 方法: 使用完整的轨迹 (Episode) 来计算真实回报 $G_t$。
• 时序差分 (TD) 方法: 使用轨迹的单步片段 $(S_t,A_t,R_{t+1},S_{t+1})$ 进行学习，无需等待一幕结束。
• 策略梯度 (PG) 方法: 通常也需要完整的轨迹来评估策略性能。
• 经验回放 (Experience Replay): 将大量轨迹的单步片段存储在回放池中，随机采样进行训练，提高样本利用率。

2. 目标：回报与折扣因子

2.1. 回报 (Return, $G_t$)

回报 (Return, $G_t$) 是在一个给定的轨迹中，从时间步 $t$ 开始，智能体未来能获得的所有奖励的总和。它衡量了从某个时间点开始，“后续的整个过程”有多好。

回报是根据智能体实际经历过的一条轨迹 $\tau =(S_0,A_0,R_1,S_1,A_1,R_2,\dots )$ 来计算的。

具体计算方式取决于任务类型：

• 对于分幕式任务 (Episodic Tasks):
  任务会在有限的时间步 $T$ 后结束。回报 $G_t$ 是从 $R_{t+1}$ 到最终奖励 $R_T$ 的简单求和。

  $$G_t=R_{t+1}+R_{t+2}+R_{t+3}+\cdots +R_T$$

  其中 $T$ 是终止状态对应的时间步。

• 对于连续性任务 (Continuing Tasks):
  任务永远不会结束 ($T\to \mathrm{\infty }$)。简单的求和可能会导致回报发散到无穷大。因此，我们必须使用下面将要介绍的折扣回报。

示例：使用轨迹计算回报

让我们回到之前的吃豆人游戏轨迹：

这是一个分幕式任务，在时间步 $T=3$ 结束。我们可以计算这条轨迹中每个时间步的回报：

• $G_0$ (从起点开始的回报): 这是整个轨迹的总奖励。
  $G_0=R_1+R_2+R_3=10+10+(-500)=-480$

• $G_1$ (从状态 $S_1$ 开始的回报):
  $G_1=R_2+R_3=10+(-500)=-490$

• $G_2$ (从状态 $S_2$ 开始的回报):
  $G_2=R_3=-500$

• $G_3$ (在终止状态 $S_3$ 的回报):
  按照惯例，终止状态之后没有未来奖励，所以回报为 0。

重要区别:

• 回报 $G_t$: 是从一条实际发生的轨迹中计算出的具体数值。它是一个样本 (sample)。
• 价值函数 $V^{\pi }(s)$: 是回报的期望值 $\mathbb{E}[G_t|S_t=s]$。它代表了从状态 $s$ 出发，遵循策略 $\pi$ 平均能获得的回报，考虑了所有可能的轨迹。

2.2. 折扣因子 (Discount Factor, $\gamma$)

为了统一分幕式和连续性任务，并反映“未来的奖励不如眼前的奖励有价值”这一经济学直觉，我们引入折扣因子 $\gamma \in [0,1]$。

• 折扣回报 (Discounted Return):

  $$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\cdots =\sum _{k=0}^{\mathrm{\infty }}{\gamma }^k{R}_{t+k+1}$$
  • 这个公式现在对两种任务类型都适用。在分幕式任务中，当 $k$ 使得 $t+k+1>T$ 时，所有后续的 $R$ 都为 0，求和自动终止。
  • 在连续性任务中，只要奖励有界且 $\gamma <1$，这个无穷级数就能保证收敛，使得回报是一个有限值。

• $\gamma$ 的作用: 通过控制 $\gamma$ 我们可以使得

  • $\gamma \to 0$ (短视): 智能体只关心即时奖励 $R_{t+1}$。
  • $\gamma \to 1$ (远视): 智能体对未来奖励和即时奖励几乎同等看待。

示例：计算折扣回报

假设 $\gamma =0.9$，我们重新计算吃豆人轨迹的回报：

• $G_2=R_3=-500$
• $G_1=R_2+\gamma G_2=10+0.9\times (-500)=10-450=-440$
• $G_0=R_1+\gamma G_1=10+0.9\times (-440)=10-396=-386$

注意，回报的计算可以写成这种方便的递归形式：$G_t=R_{t+1}+\gamma G_{t+1}$。

3. 价值函数 (Value Function)

为了评估一个策略的好坏，我们需要知道在某个状态或采取某个行动后，预期能获得多少回报。这就是价值函数的作用。

3.1. 状态价值函数 (State-Value Function, $V^{\pi }(s)$)

• 定义: 从状态 $s$ 开始，遵循策略 $\pi$，能够获得的期望回报。
• 公式:$$V^{\pi }(s)={\mathbb{E}}_{\pi }[G_t|S_t=s]$$
• 解读: $V^{\pi }(s)$ 回答了“在策略 $\pi$ 下，处于状态 $s$ 有多好？”这个问题。

3.2. 状态-行动价值函数 (Action-Value Function, $Q^{\pi }(s,a)$)

• 定义: 在状态 $s$ 下，采取行动 $a$，然后遵循策略 $\pi$，能够获得的期望回报。
• 公式:$$Q^{\pi }(s,a)={\mathbb{E}}_{\pi }[G_t|S_t=s,A_t=a]$$
• 解读: $Q^{\pi }(s,a)$ 回答了“在策略 $\pi$ 下，于状态 $s$ 采取行动 $a$ 有多好？”这个问题。$Q$ 函数通常比 $V$ 函数更有用，因为它直接告诉我们选择哪个动作更好。

3.3 联系

• $$E[G_t|S_t=s]=\sum _{a}E[G_t|S_t=s,A_t=a]\pi (a|s)$$

策略、轨迹与价值函数的关系 (The relationship between Policy, Trajectory and State Value)

3.4. 价值函数的估计：从贝尔曼方程到自举

既然价值函数是回报的期望，我们该如何从智能体的经验（轨迹）中估计它呢？核心在于利用价值函数内在的递归结构，这个结构由贝尔曼方程 (Bellman Equation) 描述。

贝尔曼期望方程 (Bellman Expectation Equation)

我们首先从折扣回报 $G_t$ 的定义出发：

通过提取公因子 $\gamma$，我们可以发现一个关键的递归关系：

这个简单的关系是所有贝尔曼方程的基石。

现在，我们对这个等式两边取期望，就能得到状态价值函数 $V^{\pi }(s)$ 之间的关系，这便是贝尔曼期望方程：

• 标量形式 (Scalar Form):
  对于任何状态 $s$，其价值等于在该状态下遵循策略 $\pi$ 能获得的期望立即奖励，加上所有可能后继状态 $s^{\prime }$ 的期望折扣价值。

  $$V^{\pi }(s)={\mathbb{E}}_{\pi }[G_t|S_t=s]={\mathbb{E}}_{\pi }[R_{t+1}+\gamma V^{\pi }(S_{t+1})|S_t=s]$$

  更具体地展开：

  $$V^{\pi }(s)=\sum _a\pi (a|s)(R(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }|s,a)V^{\pi }(s^{\prime }))$$

  这个方程揭示了一个状态的真实价值 $V^{\pi }(s)$ 与其后继状态的真实价值 $V^{\pi }(s^{\prime })$ 之间的内在联系。

• 向量形式 (Vector Form):
  如果我们将所有状态的价值视为一个向量 ${\mathbf{v}}^{\pi }$，将期望立即奖励视为向量 ${\mathbf{r}}^{\pi }$，将策略下的状态转移概率视为矩阵 ${\mathbf{P}}^{\pi }$，那么整个系统的贝尔曼期望方程可以被优雅地写成一个线性方程：

  $${\mathbf{v}}^{\pi }={\mathbf{r}}^{\pi }+\gamma {\mathbf{P}}^{\pi }{\mathbf{v}}^{\pi }$$

  这个方程存在一个解析解: ${\mathbf{v}}^{\pi }=(\mathbf{I}-\gamma {\mathbf{P}}^{\pi }{)}^{-1}{\mathbf{r}}^{\pi }$。这表明，如果环境模型已知，我们可以直接计算出价值函数。但在大多数RL问题中，模型是未知的，因此我们需要基于样本的学习方法。

方法一：蒙特卡洛 (MC) - 基于样本回报

MC 方法忽略了贝尔曼方程提供的状态间关系，它直接使用回报 $G_t$ 的定义来估计 $V^{\pi }(s)$。它通过采样大量完整的 episodes，并对每个状态访问的回报求平均值。

• 核心思想: 运行一个完整的 episode，记录下整条轨迹。对于轨迹中的每一个状态 $S_t$，我们都计算出了它后面跟着的真实回报 $G_t$。那么，这个 $G_t$ 就是对 $V^{\pi }(S_t)$ 的一个无偏估计。
• 更新方式: $V(S_t)\leftarrow V(S_t)+\alpha (G_t-V(S_t))$
• 特点:
  • 优点: 无偏 (Unbiased)。因为 $G_t$ 是对 $V^{\pi }(S_t)$ 的真实、无偏差的采样。
  • 缺点: 高方差 (High Variance)。单次轨迹的随机性很大，可能导致估计值剧烈波动。必须等待一个 episode 结束才能进行学习。

方法二：自举 (Bootstrapping) - 基于贝尔曼方程

Bootstrapping 的意思是“拔靴带”，引申为“自我提升”。在RL中，它指利用贝尔曼方程的结构，使用当前的价值估计来更新价值估计。这是时序差分 (Temporal Difference, TD) 学习方法的核心。

• 核心思想:
  贝尔曼方程告诉我们 $V^{\pi }(s)={\mathbb{E}}_{\pi }[R_{t+1}+\gamma V^{\pi }(S_{t+1})|S_t=s]$。TD 学习正是利用这一点。它不再等待整个 episode 结束来获得完整的 $G_t$，而是只走一步得到一个样本 $(S_t,A_t,R_{t+1},S_{t+1})$。然后，它用当前的、不完美的价值估计 $V(S_{t+1})$ 来构造一个对 $V^{\pi }(S_t)$ 的新估计，这个新估计被称为 TD 目标 (TD Target)。

• 学习目标 (TD Target):

  $$\text{TD Target}=R_{t+1}+\gamma V(S_{t+1})$$

  这个目标是自举的，因为它部分基于真实的样本 ($R_{t+1}$)，部分基于一个自身的旧有估计 ($V(S_{t+1})$)。

• 更新方式:
  TD 算法通过让当前的价值估计 $V(S_t)$ 朝着这个 TD 目标移动一小步来进行学习。

  $$V(S_t)\leftarrow V(S_t)+\alpha (\underset{\text{TD Target}}{\underbrace{(R_{t+1}+\gamma V(S_{t+1}))}}-V(S_t))$$

  括号中的部分 $(R_{t+1}+\gamma V(S_{t+1}))-V(S_t)$ 被称为时序差分误差 (TD Error)。

• 特点:

  • 优点: 低方差 (Low Variance)。更新不依赖于一条完整的随机轨迹，更平滑。可以在线学习 (Online)，每一步都更新，效率高。
  • 缺点: 有偏 (Biased)。因为学习目标 $V(S_{t+1})$ 本身就是一个不准确的估计。你在用一个估计去更新另一个估计。当初始估计不准时，这个偏差可能会在系统中传播。

总结:

• MC: 使用实际回报 $G_t$ 作为更新目标，直接对 $V(s)=\mathbb{E}[G_t]$ 进行采样。
• TD (Bootstrapping): 使用估计的回报 $R_{t+1}+\gamma V(S_{t+1})$ 作为更新目标，利用了 $V(s)=\mathbb{E}[R_{t+1}+\gamma V(S_{t+1})]$ 的贝尔曼关系。

这种“用估计更新估计”的自举思想是现代强化学习算法（如Q-Learning, SARSA, Actor-Critic）的基石。

对比蒙特卡洛 (MC) 与自举 (TD): 同一公式，两种哲学

我们的目标是估计状态 $S_t$ 的价值 $V(S_t)$。我们知道它的真实定义是 $V(S_t)=\mathbb{E}[G_t]$，并且回报 $G_t$ 满足递归关系：

假设我们当前处于状态 $S_t$，想要更新 $V(S_t)$。

1. 蒙特卡洛 (MC) 的计算方式：“求到底”

蒙特卡洛方法看到这个递归公式，它的处理方式是彻底展开，直到终点。

对于 MC 来说， $G_{t+1}$ 不是一个可以直接使用的值，它只是一个中间符号。要得到 $G_t$ 的具体数值，必须不断地把递归式展开：

MC 的计算流程:

1. 等待: 从 $S_t$ 开始，必须完成整个 episode，收集到未来所有的奖励 $R_{t+1},R_{t+2},\dots ,R_T$。
2. 求和: 将所有收集到的未来奖励进行折扣求和，计算出 $G_t$ 的具体、完整的样本值。
3. 更新: 使用这个完整的样本值 $G_t$ 作为 $V(S_t)$ 的学习目标。$$V(S_t)\leftarrow V(S_t)+\alpha (\underset{\text{完整的真实回报 }{G}_t}{\underbrace{(R_{t+1}+\gamma R_{t+2}+\dots )}}-V(S_t))$$

MC 的哲学: 要想知道 $G_t$ 是多少，就必须老老实实地把未来的每一步都走完，拿到每一个真实的奖励，然后加起来。它是对回报定义的直接采样。

2. 时序差分 (TD) / 自举 (Bootstrapping) 的计算方式：“信一步，靠估计”

时序差分 (TD) 方法看到同一个递归公式 $G_t=R_{t+1}+\gamma G_{t+1}$，它的处理方式是只走一步，然后用现有的估计值来近似后续部分。

对于 TD 来说，它并不关心 $G_{t+1}$ 的内部结构是什么。它做了一个大胆的假设：

"虽然我不知道 $G_{t+1}$ 的真实值是多少，但我有一个对它的期望值的估计，那就是我当前的价值函数 $V(S_{t+1})$。我就用这个估计来代替真实的 $G_{t+1}$ 吧！"

TD 的计算流程:

1. 走一步: 从 $S_t$ 开始，只需要执行一个行动，获得一个立即奖励 $R_{t+1}$ 和一个下一个状态 $S_{t+1}$。
2. 查表/估计: 查找或计算出下一个状态的当前价值估计 $V(S_{t+1})$。
3. 构建目标: 将真实的立即奖励 $R_{t+1}$ 和对未来的价值估计 $V(S_{t+1})$ 结合起来，构建一个自举的学习目标 (TD Target)。$$\text{TD Target}=R_{t+1}+\gamma V(S_{t+1})$$在这里，$V(S_{t+1})$ 被用作对 $G_{t+1}$ 的一个代理 (proxy) 或 估计 (estimate)。
4. 更新: 使用这个混合了真实与估计的目标来更新 $V(S_t)$。$$V(S_t)\leftarrow V(S_t)+\alpha (\underset{\text{TD Target, 一个估计的回报}}{\underbrace{(R_{t+1}+\gamma V(S_{t+1}))}}-V(S_t))$$

TD 的哲学: 我不需要知道未来的所有细节。我只需要知道我下一步能得到的真实奖励，以及我相信的、从那以后能得到的总价值。我用我当前的信念 (current belief) 来更新我之前的信念 (previous belief)。

总结对比

4. 贝尔曼方程 (Bellman Equations)

贝尔曼方程是 RL 中最重要的公式之一，它将一个状态的价值与其后继状态的价值关联起来，提供了迭代求解价值函数的方法。

4.1. 贝尔曼期望方程 (Bellman Expectation Equation)

• $V^{\pi }$ 的贝尔曼方程:

  $$V^{\pi }(s)=\sum _a\pi (a|s)\sum _{s^{\prime }}P(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma V^{\pi }(s^{\prime })]$$$$\Rightarrow V_{\pi }(s)=\sum _a\pi (a|s)[\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)V_{\pi }(s^{\prime })]$$$$\Rightarrow q_{\pi }(s,a)=\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)V_{\pi }(s^{\prime })$$$$V^{\pi }(s)=\underset{\text{期望的立即奖励}}{\underbrace{\sum _a\pi (a|s)[\sum _{r}p(r|s,a)r]}}+\gamma \underset{\text{期望的未来价值}}{\underbrace{\sum _a\pi (a|s)\sum _{s^{\prime }}p(s^{\prime }|s,a)V^{\pi }(s^{\prime })}}$$$$=\sum _a\pi (a|s)(\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)V^{\pi }(s^{\prime }))$$$$=r_{\pi }(s)+\gamma \sum _{s^{\prime }}{p}_{\pi }(s^{\prime }|s)v_{\pi }(s^{\prime })$$

  两个贝尔曼公式的互推 (The mutual derivation of two Bellman formulas)

  • 当前状态的价值 = 所有可能行动的期望价值。
  • 某个行动的价值 = 所有可能后继状态的（即时奖励 + 折扣后的未来价值）的期望。

• $Q^{\pi }$ 的贝尔曼方程:

  $$Q^{\pi }(s,a)=\sum _{s^{\prime }}P(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma \sum _{a^{\prime }}\pi (a^{\prime }|s^{\prime })Q^{\pi }(s^{\prime },a^{\prime })]$$

4.2. 贝尔曼最优方程 (Bellman Optimality Equation)

最优策略 ${\pi }^{\ast }$ 对应最优价值函数 $V^{\ast }$ 和 $Q^{\ast }$。

• $V^{\ast }$ 的贝尔曼最优方程:

  $$V^{\ast }(s)=\underset{a}{max}\sum _{s^{\prime }}P(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma V^{\ast }(s^{\prime })]$$
  • 最优状态价值等于所有行动中能带来的最大期望回报。

• $Q^{\ast }$ 的贝尔曼最优方程:

  $$Q^{\ast }(s,a)=\sum _{s^{\prime }}P(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma \underset{a^{\prime }}{max}{Q}^{\ast }(s^{\prime },a^{\prime })]$$
  • 如果知道了最优 $Q^{\ast }$ 函数，那么最优策略就是贪心策略 (Greedy Policy)：$${\pi }^{\ast }(s)=\arg \underset{a}{max}{Q}^{\ast }(s,a)$$

RL 算法的核心任务，就是通过各种方法求解贝尔曼最优方程，找到 $Q^{\ast }$ 或 ${\pi }^{\ast }$。

How to solve two unknowns from one equation

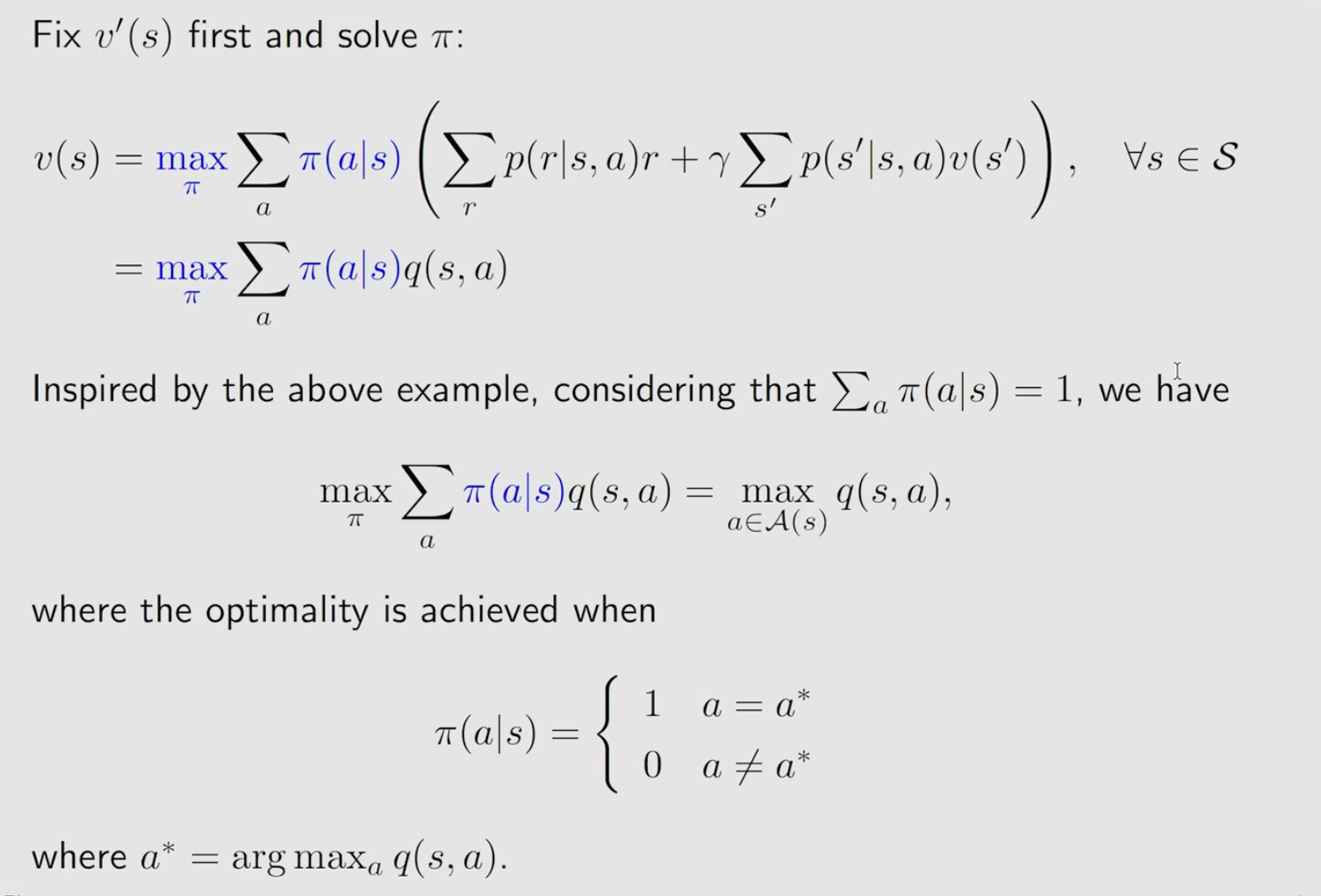
4.3 贝尔曼最优方程 (Bellman Optimality Equation, BOE) 与求解

在我们介绍了用于评估一个给定策略的贝尔曼期望方程之后，现在我们来看如何寻找最优策略。这需要用到贝尔曼最优方程 (BOE)。

BOE 的核心思想是：最优策略下的价值函数，必须等于在所有可能的单步行动中，选择那个能带来最大期望回报的行动所对应的价值。

4.3.1 BOE 的两种形式：V* 和 Q*

首先，我们将最优价值函数记为 v*，它代表了在所有策略中能达到的最大期望回报。

状态价值函数的最优方程 (BOE for v)*

正如图片第一行所示，v*(s) 必须满足以下条件：

这个方程和贝尔曼期望方程非常像，唯一的区别是把期望算子 Σ_a π(a|s) 换成了最大化算子 max_a。它表示最优价值等于选择最优单步行动 a 后能得到的期望回报。

行动价值函数的最优方程 (BOE for q)*

为了更好地理解这个方程，我们引入最优行动价值函数 q*(s, a)。

• q*(s, a)：在状态 s 采取行动 a，然后从那以后都遵循最优策略所能得到的期望回报。$$q^{\ast }(s,a)=\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v^{\ast }(s^{\prime })$$这正是图片中第一个方程括号里的那部分！

将 q* 代入 v* 的方程，我们得到一个至关重要的关系：

直观理解：一个状态的最优价值，等于在这个状态下所有可选行动的“最优Q值”中，最大的那一个。

4.3.2 最优策略的真面目：贪心策略

现在，我们来看图片中最关键的推导，它揭示了最优策略 π* 的形式。

我们从 v* 的另一个定义出发：

这个式子问的是：“什么样的策略 π 能够最大化 q* 值的加权平均？”

核心洞察 (图片中的推导):

• 问题: 我们要最大化一个加权平均 Σ π(a|s)q*(s,a)，其中权重 π(a|s) 是概率（非负且和为1）。
• 类比: 想象你有 100 块钱（总概率为1），要投资到几个回报率不同（q*(s,a) 值不同）的项目（行动 a）中去。为了让总收益最大，你会怎么投资？
• 答案: 你会把所有钱（100%的概率）都投到那个回报率最高的项目（q* 值最大的行动 a*）上。
• 结论:$$\underset{\pi }{max}\sum _a\pi (a|s)q^{\ast }(s,a)=\underset{a}{max}{q}^{\ast }(s,a)$$这个最大值是在一个确定性的、贪心的策略下取得的。

这个推导告诉我们一个惊人的事实：

对于任何 MDP，至少存在一个最优策略是确定性的。这个策略就是简单地在每个状态下，选择那个具有最大 q* 值的行动。

最优策略 π* 的形式:

4.3.3 总结与应用

这个发现是强化学习的基石之一：

1. 目标简化: 我们寻找最优策略 π* 的问题，被转化为了寻找最优行动价值函数 q* 的问题。
2. 决策简化: 一旦我们通过某种方式（例如，价值迭代或 Q-Learning）得到了 q*，那么在任何状态 s 下，最优的决策就是简单地执行 argmax_a q*(s, a)，无需再进行复杂的规划。

这解释了为什么 Q-Learning 算法的核心是学习一个 Q-table：因为这个 Q-table（对 q* 的估计）已经隐式地包含了最优策略的所有信息。

4.4 求解贝尔曼方程：压缩映射理论

我们已经知道，最优价值函数 v* 必须满足贝尔曼最优方程 (BOE)。但这个方程形式复杂，我们如何能确定它有解？解是否唯一？又该如何找到这个解？

要回答这些问题，我们需要借助强大的数学工具。这张图片中介绍的两个概念正是解答这一切的钥匙。

4.4.1 核心数学概念详解

不动点 (Fixed Point)

• 定义: 正如图片所示，对于一个函数（或更广义的“算子”、“变换”）f，如果将它作用于某个点 x 后，得到的结果仍然是 x 本身，那么 x 就是 f 的一个不动点。

  $$f(x)=x$$

• 直观理解: 想象一个函数 f 是对空间中所有点的一次移动。不动点就是在这次移动中纹丝不动的那个点。

• 与强化学习的联系: 我们可以将贝尔曼最优方程视为一个不动点问题。定义一个贝尔曼最优算子 T，它的作用就是对任意一个价值函数 v 进行一次贝尔曼更新：

  $$T(v)(s)=\underset{a}{max}(\sum _{r,s^{\prime }}p(s^{\prime },r|s,a)[r+\gamma v(s^{\prime })])$$

  那么，贝尔曼最优方程 v* = T(v*) 就可以被理解为：最优价值函数 v* 正是贝尔曼最优算子 T 的不动点。我们的目标，就是找到这个算子的不动点。

压缩映射 (Contraction Mapping)

• 定义: 一个函数 f 如果是压缩映射，意味着将它作用于任意两个不同的点 x₁ 和 x₂ 后，新产生的两个点 f(x₁) 和 f(x₂) 之间的距离，会比原来两点间的距离严格地缩小。

  $$\parallel f(x_1)-f(x_2)\parallel \le \gamma \parallel x_1-x_2\parallel$$

  其中，压缩因子 γ 是一个介于 [0, 1) 之间的常数。

• 直观理解: 压缩映射就像一个能把整个空间“向内挤压”的变换。无论你从空间中哪两个点开始，只要经过一次 f 变换，它们之间的距离就会至少缩短 γ 倍。反复进行这个变换，整个空间中的所有点最终都会被“挤”向同一个点。

• 关键要素:

  • γ 必须严格小于 1。这是保证“压缩”效果的关键。如果 γ=1，距离可能保持不变（例如旋转），就无法保证收敛。
  • || ⋅ || 是范数 (norm)，代表了一种测量向量间“距离”的方式。这个理论的强大之处在于它对任何一种常见的距离度量方式（如欧几里得距离、曼哈顿距离等）都成立。

4.4.2 巴拿赫不动点定理 (Banach Fixed-Point Theorem)

这个定理是连接以上两个概念的桥梁，它给出了一个惊人的结论：

在一个完备的度量空间中，任何一个压缩映射都拥有一个且仅有一个唯一的不动点。

此外，从空间中的任意一个初始点 x₀ 出发，通过反复迭代 x_{k+1} = f(x_k)，所得到的序列必然会收敛到这个唯一的不动点，且为指数级别的收敛速度。

4.4.3 理论与强化学习的完美结合

现在，我们可以将所有碎片拼凑起来了。核心结论是：

可以证明，贝尔曼最优算子 T 正是一个以折扣因子 γ 为压缩因子的压缩映射。

基于这个事实和巴拿赫不动点定理，我们得到了关于强化学习的三个根本性保证：

1. 解的存在且唯一 (Existence and Uniqueness)
   因为 T 是一个压缩映射，所以它必然存在一个唯一的不动点。这意味着最优价值函数 v* 不仅存在，而且是唯一的。我们寻找的目标是明确且唯一的。

2. 价值迭代算法的收敛性保证 (Convergence Guarantee)
   定理保证了从任意点开始的迭代序列 v_{k+1} = T(v_k) 必将收敛到不动点 v*。而这正是价值迭代 (Value Iteration) 算法的数学形式！这从理论上证明了，只要我们不断地用贝尔曼最优方程去更新价值函数，最终一定能得到正确的最优价值函数。

3. 对初始值的无关性 (Independence of Initialization)
   我们可以从任意一个初始价值函数 v₀（比如，一个全零的向量）开始迭代，最终都会收敛到同一个 v*。这使得算法的实现非常鲁棒。

总结：压缩映射理论为强化学习提供了一块坚实的数学基石。它告诉我们，v* 的求解问题是良定 (well-posed) 的，并且像价值迭代这样的朴素算法是保证有效的。折扣因子 γ 在这里扮演了至关重要的数学角色——正是它确保了贝尔曼算子的压缩性质，从而保证了整个理论框架的成立。

好的，这是一个非常重要且具有深刻实践意义的定理，它被称为**“奖励整形 (Reward Shaping)”** 的理论基础之一。这个定理告诉我们，在什么情况下改变奖励函数不会改变最终的最优策略。

我会将它作为 4.4 节加入到贝尔曼最优方程的讨论之后，因为它正是建立在 BOE 的基础上的。

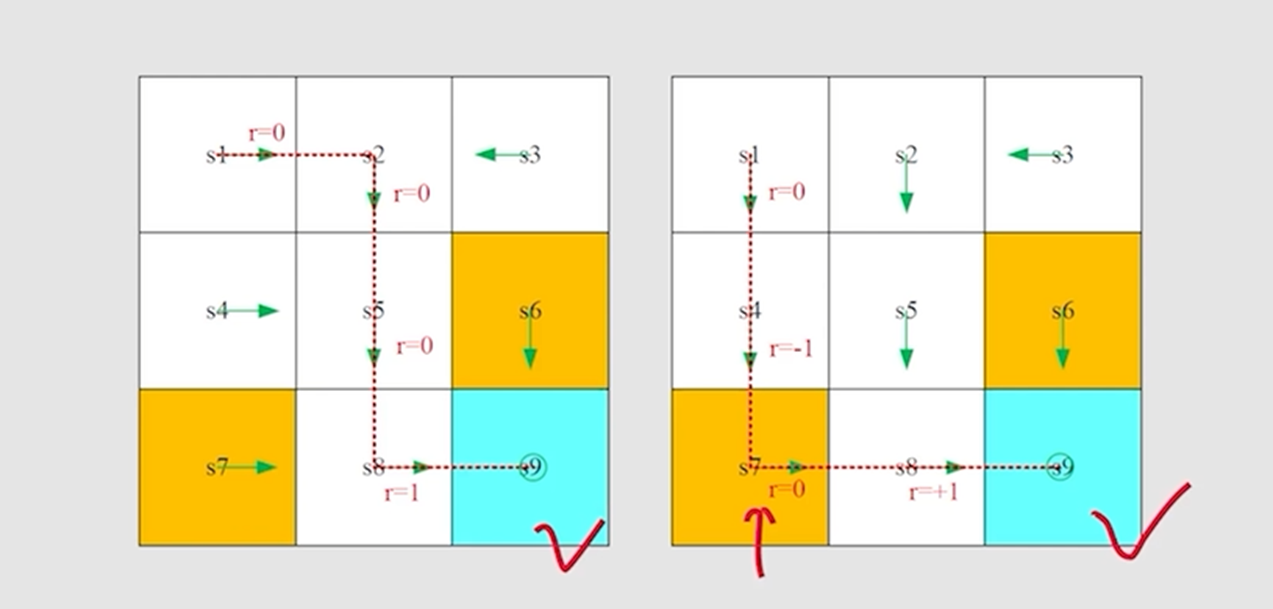
4.5 定理：最优策略的仿射变换不变性 (Optimal Policy Invariance)

我们已经知道，奖励函数 R 是我们与智能体沟通目标的接口。一个自然的问题是：如果我们改变了奖励函数，最优策略会如何变化？这个定理给出了一个强有力的答案。

定理 (最优策略不变性)

如果我们将环境中的每一个奖励 r 都进行一次仿射变换 (Affine Transformation)，从 r 变为 a*r + b（其中 a 是一个正数常量，b 是任意实数常量），那么：

1. 新的最优价值函数 v' 是原最优价值函数 v* 的一个线性变换。
2. 最优策略 π* 保持完全不变。

数学表述

• 前提:

  • 原 MDP 的奖励为 r，最优价值函数为 v*。
  • 新的 MDP 的奖励为 r' = a*r + b，其中 a > 0，b 是常数。其最优价值函数为 v'。

• 结论 1 (价值函数的变化):
  新的最优价值函数 v' 与旧的 v* 之间的关系为：

  $${\mathbf{v}}^{\prime }=a{\mathbf{v}}^{\ast }+\frac{b}{1-\gamma }\mathbf{1}$$

  其中，1 是一个所有元素都为 1 的向量。这意味着每个状态的价值都被缩放了 a 倍，并加上了一个常量 b / (1-γ)。

• 结论 2 (策略的不变性):

  $${\pi }_{\ast }^{\prime }={\pi }^{\ast }$$

  两个 MDP 的最优策略是完全相同的。

直观理解与为什么成立

为什么会这样？关键在于最优策略只关心不同行动之间的“相对好坏”，而不关心它们的“绝对价值”。

最优策略 π*(s) 是通过 argmax_a q*(s, a) 来决定的。我们来看看 q*(s, a) 在奖励变换后会发生什么变化。

• 原 q*(s, a): 依赖于 r 和 v*
• 新 q'(s, a): 依赖于 r' 和 v'$$q^{\prime }(s,a)=\mathbb{E}[a\ast r+b+\gamma v^{\prime }]=a\cdot \mathbb{E}[r+\gamma v\ast ]+b+\frac{\gamma b}{1-\gamma }=a\cdot q^{\ast }(s,a)+\frac{b}{1-\gamma }$$（经过一些代数推导）

我们可以看到，新的 Q 函数 q' 也是旧 Q 函数 q* 的一个线性变换：q'(s, a) = a * q*(s, a) + C，其中 C 是一个不依赖于行动 a 的常量。

关键洞察:
对一个函数的所有值都乘以一个正常数 a 并加上一个常量 C，并不会改变哪个输入能让函数取得最大值。

由于 argmax 不变，所以从 q* 推导出的最优策略 π* 也就保持不变。

实践意义 (奖励整形 Reward Shaping)

这个定理在实践中非常有用：

1. 奖励归一化: 我们可以放心地将奖励缩放（例如，归一化到 [-1, 1] 区间），这有助于稳定神经网络的训练，而不用担心会改变问题的本质。
2. 避免稀疏奖励: 在很多问题中，奖励非常稀疏（大部分时间奖励为0）。我们可以给每一步都加上一个小的负奖励 b < 0（例如 -0.01），来鼓励智能体尽快找到目标，而不会改变找到目标的最优路径。这个 -0.01 就是常数 b。
3. 理论指导: 它为我们设计和修改奖励函数提供了理论指导，让我们知道什么样的修改是“安全”的（不改变最优策略），什么样的修改会从根本上改变问题。

5. 求解贝尔曼最优方程：动态规划

我们已经有了贝尔曼最优方程，并且有理论保证它存在唯一解。那么，如何具体地求解它呢？当环境模型（即状态转移概率 P 和奖励函数 R）已知时，我们可以使用动态规划 (Dynamic Programming, DP) 的方法来精确求解。价值迭代和策略迭代是两种最核心的 DP 算法。

5.1 价值迭代 (Value Iteration, VI)

价值迭代算法的核心思想，正是我们之前讨论的巴拿赫不动点定理的直接应用。不动点定理告诉我们，只要反复应用一个压缩映射，无论从哪里开始，最终都会收敛到那个唯一的固定点。

核心思想：
价值迭代通过反复迭代贝尔曼最优方程，将当前的价值函数 v_k “更新”成一个更好的价值函数 v_{k+1}，直到这个过程收敛。收敛时，我们就得到了最优价值函数 v*。

算法流程:

1. 初始化: 任意初始化一个价值函数向量 v₀ (通常是全零向量)。

2. 迭代循环: 对于 k = 0, 1, 2, ...，重复以下步骤：

   • 对于每一个状态 s ∈ S，根据贝尔曼最优方程进行更新：$$v_{k+1}(s)\leftarrow \underset{a}{max}(R(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }|s,a)v_k(s^{\prime }))$$
     • 关键点: 注意我们是用第 k 次的价值函数 v_k 来计算第 k+1 次的价值函数 v_{k+1}。这正是在反复应用贝尔曼最优算子 T：v_{k+1} = T(v_k)。

3. 终止条件: 当价值函数的改变量足够小时，即 max_s |v_{k+1}(s) - v_k(s)| < ε（其中 ε 是一个很小的正数），则停止迭代。此时，我们认为 v_{k+1} ≈ v*。

4. 提取最优策略: 当价值函数收敛到 v* 后，我们可以通过一次“向前看”来提取出最优策略 π*：

   $${\pi }^{\ast }(s)=\arg \underset{a}{max}(R(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }|s,a)v^{\ast }(s^{\prime }))$$

5.2 策略迭代 (Policy Iteration, PI)

策略迭代提供了另一种求解思路。它不像价值迭代那样直接在价值空间中寻找最优解，而是在策略空间中进行搜索。它由两个交替进行的步骤组成：策略评估和策略提升。

核心思想：
从一个任意的策略开始，不断地“评估这个策略有多好”，然后“根据评估结果找到一个更好的策略”，如此循环往复，直到策略不再变化，此时就找到了最优策略。

算法流程:

1. 初始化: 任意初始化一个策略 π₀。

2. 迭代循环: 对于 k = 0, 1, 2, ...，重复以下步骤：

   • a) 策略评估 (Policy Evaluation):

     • 目标: 计算当前策略 π_k 的真实价值函数 v_{π_k}。
     • 方法: 求解该策略下的贝尔曼期望方程。$$v_{{\pi }_k}(s)=R(s,{\pi }_k(s))+\gamma \sum _{s^{\prime }}P(s^{\prime }|s,{\pi }_k(s))v_{{\pi }_k}(s^{\prime })$$这通常通过迭代的方式求解，直到 v 收敛（这本身就是一个小的价值迭代过程），或者通过矩阵求逆 v_{π_k} = (I - γP_{π_k})⁻¹ r_{π_k} 直接计算。

   • b) 策略提升 (Policy Improvement):

     • 目标: 基于刚刚计算出的价值函数 v_{π_k}，找到一个比 π_k 更好（或一样好）的新策略 π_{k+1}。
     • 方法: 对每一个状态 s，我们贪心地选择能够最大化期望回报的行动：$${\pi }_{k+1}(s)\leftarrow \arg \underset{a}{max}(R(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }|s,a)v_{{\pi }_k}(s^{\prime }))$$

3. 终止条件: 如果新策略与旧策略完全相同（π_{k+1} = π_k），那么算法收敛，此时的策略就是最优策略 π*，其对应的价值函数就是 v*。

5.3 价值迭代 vs. 策略迭代

5.4 广义策略迭代 (Generalized Policy Iteration, GPI) 与截断策略迭代

策略迭代和价值迭代看似不同，但它们都遵循一个共同的模式，被称为广义策略迭代 (Generalized Policy Iteration, GPI)。GPI 指的是任何将策略评估 (Policy Evaluation) 和策略改进 (Policy Improvement) 交织在一起进行的方法。

• 策略评估 (PE): 使当前的价值函数 v 趋向于当前策略 π 的真实价值 v_π。
• 策略改进 (PI): 使当前的策略 π 对于当前的价值函数 v 变得更贪心。

在这个 GPI 框架下，PI 和 VI 只是两个特例。

截断策略迭代 (Truncated Policy Iteration)

核心思想：我们不必在每次策略评估（PE）步骤中都等到价值函数完全收敛。我们可以只进行固定次数 m 的迭代，然后就进入策略改进（PI）步骤。

这种方法就被称为截断策略迭代 (Truncated Policy Iteration)。

算法流程:

1. 初始化: 从一个任意的策略 π₀ 和价值函数 v₀ 开始。
2. 循环:
   • a) 截断策略评估 (Truncated PE):
     • 目标: 对当前策略 π_k 进行不完全的评估。
     • 方法: 从 v_k 开始，使用贝尔曼期望方程迭代 m 次：

       v_temp = v_k
       for _ in range(m):
           v_temp = r_{π_k} + γ * P_{π_k} * v_temp
       # 经过 m 次更新后，得到一个对 v_{π_k} 的近似
       v_{k+1} = v_temp
       

   • b) 策略改进 (PI):
     • 目标: 基于这个近似的价值函数 v_{k+1}，找到一个贪心的新策略 π_{k+1}。
     • 方法:$${\pi }_{k+1}(s)=\arg \underset{a}{max}(R(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }|s,a)v_{k+1}(s^{\prime }))$$
3. 终止: 直到策略或价值函数收敛。

为什么截断策略迭代是更广义的框架？

截断策略迭代通过调整参数 m（即评估步骤的迭代次数），可以无缝地变为策略迭代或价值迭代。

• 当 m -> ∞ (评估到完全收敛):

  • v_{k+1} 会精确地等于当前策略 π_k 的真实价值 v_{π_k}。
  • 此时，截断策略迭代就等价于标准的策略迭代 (Policy Iteration)。

• 当 m = 1 (只评估一次):

  • 评估步骤变为：v_{k+1} = r_{π_k} + γ * P_{π_k} * v_k。
  • 而改进步骤是：π_{k+1} = argmax based on v_{k+1}。
  • 这个过程虽然看起来还是两步，但我们可以把 π_k 和 v_{k+1} 这两个式子合并。将 π_k 的贪心定义代入，实际上它等价于价值迭代的核心更新步骤：$$v_{k+1}\leftarrow \underset{a}{max}(R(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }|s,a)v_k(s^{\prime }))$$
  • 因此，当 m=1 时，截断策略迭代就等价于价值迭代 (Value Iteration)。

总结与实践意义

• 一个统一的谱系: 截断策略迭代将 PI 和 VI 统一到了一个算法谱系中。

  • 谱系的一端 (m=1): 价值迭代，每次评估都很“粗糙”，但更新很快。
  • 谱系的另一端 (m=∞): 策略迭代，每次评估都“完美”，但成本高昂。
  • 中间地带 (1 < m < ∞): 提供了在计算成本和收敛速度之间的灵活权衡。

• 实践中的优势: 在许多大规模问题中，我们既不想承担策略迭代中完全评估的巨大计算开销，也不想忍受价值迭代可能需要的非常多次的迭代。选择一个适中的 m 值（例如 m=5 或 m=10）进行截断策略迭代，通常是最快达到最优策略的方法。它在每次迭代中都取得了显著的进步，同时又控制了单次迭代的计算成本。

6. RL 算法分类

6.1 Model-Based vs. Model-Free

• 基于模型 (Model-Based): 智能体尝试学习或已知环境的模型（即状态转移概率 $P$ 和奖励函数 $R$），然后利用模型进行规划（如动态规划）。
• 无模型 (Model-Free): 智能体不学习环境模型，直接通过与环境的交互经验来学习策略或价值函数。这是目前更主流的方法。

6.2 Value-Based vs. Policy-Based

• 基于价值 (Value-Based): 学习价值函数（通常是 $Q$ 函数），然后根据价值函数隐式地得到策略（如贪心策略）。
  • 代表算法: Q-Learning, Sarsa, DQN。
• 基于策略 (Policy-Based): 直接学习策略函数 $\pi (a|s)$，即直接参数化策略。
  • 代表算法: REINFORCE, Policy Gradients。
• 演员-评论家 (Actor-Critic): 结合以上两者。Actor (演员) 负责学习策略，Critic (评论家) 负责学习价值函数来评估 Actor 的表现，并指导其更新。
  • 代表算法: A2C, A3C, DDPG, SAC。

6.3 On-Policy vs. Off-Policy

• 同策略 (On-Policy): 学习和决策使用同一个策略。即用来评估和改进的策略，就是当前智能体正在执行的策略。
  • 特点: 稳健，但探索性差，样本利用率低。
  • 代表算法: Sarsa, A2C。
• 异策略 (Off-Policy): 学习和决策使用不同的策略。智能体可以利用过去（甚至其他智能体）的经验数据来学习当前的目标策略。
  • 特点: 样本利用率高，探索性强，但可能不稳定。
  • 代表算法: Q-Learning, DQN, DDPG。

7. 蒙特卡洛（MC）强化学习算法

蒙特卡洛（Monte Carlo, MC）方法是强化学习中一类非常重要的 无模型（Model-Free） 算法。

核心思想：它不依赖于环境模型（即不知道状态转移概率 P 和奖励函数 R），而是通过与环境交互，从完整的、有始有终的“回合”（Episode）中学习。智能体必须跑完一整个回合，拿到最终的奖励，然后回头更新这一路上所做的决策的价值。

7.1. 广义策略迭代 (GPI) - 无模型学习的核心框架

在进入具体算法之前，我们需要理解一个统一所有强化学习方法的核心思想——广义策略迭代 (Generalized Policy Iteration, GPI)。

• 它不是一个具体的算法，而是一个通用的框架或思想。
• 核心思想: GPI 指的是策略评估 (Policy Evaluation) 和策略改进 (Policy Improvement) 这两个过程相互作用、交替进行的通用模式。

GPI 的两个组成部分

1. 策略评估 (Policy Evaluation):

   • 目标: 估计当前策略 π 的价值函数 (v_π 或 q_π)。
   • 在无模型设定下，我们无法直接计算，只能通过采样（例如，运行很多次游戏，取平均分）来近似估计。

2. 策略改进 (Policy Improvement):

   • 目标: 基于当前的价值估计，通过变得对价值函数更贪心 (greedy) 来找到一个更好的策略 π'。
   • 这个过程和之前一样，即 π'(s) = argmax_a q(s,a)。

GPI 的工作机制

这两个过程相互竞争又相互协作，最终将策略和价值函数推向最优：

• 评估驱使价值函数 v 与当前策略 π 保持一致。
• 改进驱使策略 π 与当前价值函数 v 变得贪心，从而打破之前的一致性。

可以想象策略和价值函数在跳一支双人舞，它们不断调整自己以适应对方。只要我们保证两个过程都在不断进行（不要求任何一方必须完全收敛），最终整个系统就会收敛到一个稳定的平衡点。在这个平衡点，价值函数与策略完全一致，同时策略相对于价值函数也是贪心的，此时我们就找到了最优策略 π* 和最优价值函数 v*。

GPI 的普适性

GPI 是一个极其通用的框架。

• 我们之前讨论的策略迭代是 GPI 的一个特例，其中“评估”步骤被执行到完全收敛。
• 我们之前讨论的价值迭代也是 GPI 的一个特例，其中“评估”步骤被截断为只迭代一次。
• 接下来要介绍的所有无模型控制算法，如蒙特卡洛控制和Q-Learning，也都可以被看作是 GPI 的具体实现。它们只是在“如何用样本进行策略评估”这一点上有所不同。

7.2 最简单的MC算法：MC Basic (用于策略评估)

这里的 "MC Basic" 通常指的是蒙特卡洛策略评估（MC Policy Evaluation），即在给定一个策略 π 的情况下，计算出这个策略的状态价值函数 V(s)。

• 目标：评估一个固定策略 π 的好坏。

• 算法流程：

  1. 遵循策略 π：让智能体（Agent）根据给定的策略 π 玩一整个回合（Episode），从开始到结束，记录下整个轨迹（状态、动作、奖励序列）。
  2. 计算回报（Return）：对于这个回合中第一次出现的每一个状态 s，计算从这个状态开始直到回合结束所获得的累积奖励 G_t。
     • G_t = R_{t+1} + γR_{t+2} + ... (其中 γ 是折扣因子)
     • 这被称为 首次访问MC（First-Visit MC）。也可以用每次访问MC（Every-Visit MC），即计算每次访问该状态时的回报。通常用前者。
  3. 更新价值：将计算出的回报 G_t 更新到状态 s 的价值估计中。最简单的方法是直接求平均值。
     • V(s) ← average(Returns(s))
  4. 重复：重复以上步骤很多次回合，根据大数定律，V(s) 会逐渐收敛到真实的价值。

• 局限性：

  • 这只是一个评估算法，它只能告诉你一个策略有多好，但不能帮你找到更好的策略。
  • 为了找到最优策略，我们需要进入“控制”阶段。

MC Based

7.3 更高效地利用数据：MC Exploring Starts (用于策略控制)

为了找到最优策略（控制问题），我们需要评估动作价值函数 Q(s, a)，而不仅仅是 V(s)。但这里有一个关键问题：如果我们当前的策略从不在某个状态 s 尝试动作 a，我们就永远无法知道 Q(s, a) 的值，也就无法改进策略。

“探索性开端”（Exploring Starts, ES） 就是为了解决这个问题而提出的一种强力假设。

• 目标：在保证充分探索的前提下，找到最优策略。
• 核心假设 (Exploring Starts)：在每一回合开始时，我们随机选择一个状态 s 和一个动作 a作为起点，然后才开始遵循当前策略。
• 为什么“更高效”：这个假设保证了所有的状态-动作对 (s, a) 都有机会被访问到。这样一来，我们收集到的数据就能覆盖所有可能性，从而可以准确地评估每一个 Q(s, a)，最终找到全局最优解。
• 算法流程（MC ES 控制算法）：
  1. 初始化一个随机的 Q(s, a) 表和一个基于它的确定性策略 π。
  2. 循环（很多回合）：
     a. 使用 探索性开端 开始一个新回合（随机选择 s 和 a）。
     b. 根据当前策略 π 完成该回合。
     c. 计算回合中每个 (s, a) 对的回报 G_t。
     d. 更新 Q(s, a) ← average(Returns(s, a))。
     e. 策略改进：在每个回合结束后，根据更新后的 Q 表来改进策略。对于每个状态 s，让新的策略选择能使 Q(s, a) 最大化的那个动作 a。
     • π(s) ← argmax_a Q(s, a)
• 局限性：
  • 不切实际：“探索性开端”这个假设在现实世界中往往是无法实现的。例如，你不能让一个机器人凭空出现在某个特定的姿势（状态）并强制它执行某个动作（动作）来开始任务。

The comparison of DP, MC and TD

7.4 移除探索性开端：MC ε-Greedy (更实用的策略控制)

既然“探索性开端”不实用，我们就需要一种新的方法来确保在与环境交互的过程中，智能体能自己进行探索。ε-贪心（Epsilon-Greedy） 策略就是最常用和最简单的方法。

• 目标：在没有探索性开端假设的情况下，找到最优策略。

• 核心思想：平衡 探索（Exploration） 和 利用（Exploitation）。

  • 利用：在绝大多数时间（概率 1-ε）里，选择当前看来最好的动作（即 Q(s, a) 值最大的那个 a）。
  • 探索：在少数时间（概率 ε）里，随机选择一个动作，给其他“看起来不那么好”的动作一个机会，万一它们其实更好呢？

• 算法流程 (On-Policy MC Control with ε-Greedy)：

  1. 初始化一个随机的 Q(s, a) 表。
  2. 基于这个 Q 表，构建一个 ε-贪心策略 π。
  3. 循环（很多回合）：
     a. 使用当前的 ε-贪心策略 π 来生成一个完整的回合（这次是从固定的起始状态开始）。
     b. 计算回合中每个 (s, a) 对的回报 G_t。
     c. 更新 Q(s, a) ← average(Returns(s, a))。
     d. 策略自动改进：因为我们的策略 π 是直接基于 Q 表的（ε-贪心），所以当我们更新了 Q 表后，策略 π 的行为也自动地被改进了。下一次它在做决策时，就会参考新的 Q 值。

• 优势：

  • 实用性强：不再需要不切实际的假设，适用于各种环境。
  • 保证收敛：理论上可以证明，只要 ε 大于0，并且我们不断更新，这个算法最终能收敛到最优策略。

总结与演进关系

1. MC Basic：只能评估一个给定的策略，无法改进它。
2. MC Exploring Starts：为了改进策略，引入了“探索性开端”的强假设来保证充分探索，从而能学习最优策略。
3. MC ε-Greedy：抛弃了不切实际的“探索性开端”假设，通过在策略层面引入随机性（ε-贪心），实现了实用且有效的探索，是真正能在实际问题中应用的MC控制算法。