1. 机器学习基本概念 (Basic Concepts)

Video: https://www.youtube.com/watch?v=Ye018rCVvOo

1.1 主要机器学习任务类型 (Major Types of Machine Learning Tasks)

机器学习算法可以根据其学习目标和所处理的数据类型大致分为以下几类：

1. 监督学习 (Supervised Learning)

   • 目标: 从带标签的训练数据（即每个数据点都有一个已知的“答案”或“目标输出”）中学习一个映射函数，以便对新的、未见过的数据进行预测。
   • 子类型:
     • 回归 (Regression):
       • 目标输出: 连续的数值 (a continuous scalar value)。
       • 例子: 预测房价、股票价格、温度。
         
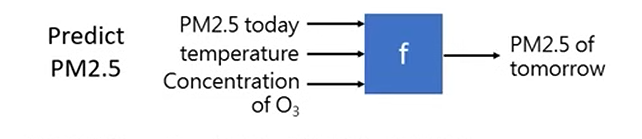
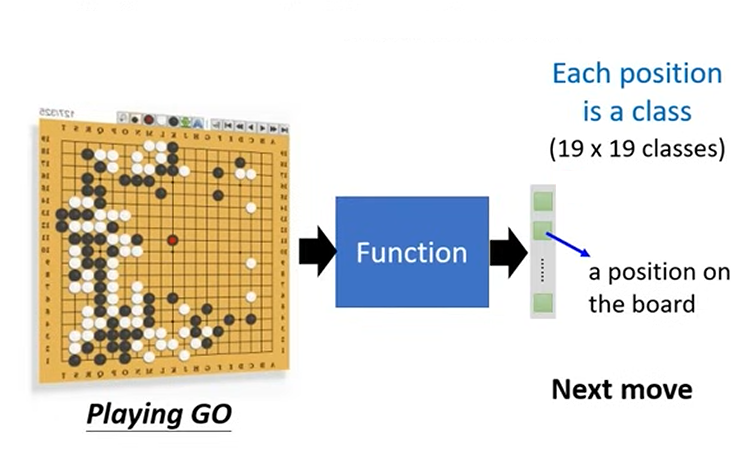
     • 分类 (Classification):
       • 目标输出: 离散的类别标签 (a discrete class label) from a predefined set.
       • 例子: 图像识别（猫/狗）、邮件分类（垃圾/非垃圾）、疾病诊断（有病/无病）。
         

2. 无监督学习 (Unsupervised Learning)

   • 目标: 从未带标签的数据中发现隐藏的模式、结构或关系。算法自行探索数据。
   • 子类型:
     • 聚类 (Clustering):
       • 目标: 将数据点分组成相似的集合（簇），使得同一簇内的数据点相似度高，不同簇之间的数据点相似度低。
       • 例子: 客户分群、异常检测。
     • 降维 (Dimensionality Reduction):
       • 目标: 减少数据特征的数量，同时保留重要信息，以便于可视化、提高效率或减少噪声。
       • 例子: 主成分分析 (PCA)、t-SNE。
     • 关联规则学习 (Association Rule Learning):
       • 目标: 发现数据项之间的有趣关系或关联。
       • 例子: 购物篮分析（“购买面包的人也倾向于购买牛奶”）。
     • **(概率)结构学习 (Probabilistic Structure Learning / Graphical Model Learning)
     • (部分属于此类):
       • 目标: 发现一组随机变量之间的概率依赖关系，并用图结构（如贝叶斯网络、马尔可夫网络）来表示这些关系。
       • 特性: 当没有预先指定变量间的关系，而是从数据中推断这些关系时，这通常被视为一种无监督的发现过程。它可以帮助理解数据的内在结构和生成机制。
       • 例子: 从基因表达数据中推断基因调控网络，从传感器数据中学习变量间的依赖。

3. 强化学习 (Reinforcement Learning)

   • 目标: 智能体 (agent) 通过与环境 (environment) 交互来学习如何做出决策，以最大化累积奖励 (cumulative reward)。智能体通过试错来学习最优策略。
   • 例子: 训练机器人行走、棋类游戏AI (AlphaGo)、自动驾驶策略。

1.2 机器学习的步骤 (Steps in Machine Learning)

1.2.1 定义一个带有未知参数的函数/模型 (Define a Function/Model with Unknown Parameters)

机器学习的核心任务之一是从数据中学习一个函数（或模型），该函数能够很好地描述输入和输出之间的关系，或者发现数据中的潜在结构。这个函数通常包含一些未知参数 (unknown parameters)，这些参数的值需要从训练数据中学习得到。

以一个简单的线性回归模型为例：

这里：

• $y$ 是我们想要预测的目标输出 (target output)。
• $x_1$ 是一个输入特征 (input feature)。
• $w$ (权重, weight) 和 $b$ (偏置, bias) 是模型的未知参数。我们的目标就是通过学习算法，利用训练数据来找到最优的 $w$ 和 $b$ 的值。

1.2.2 定义代价函数/损失函数以评估模型 (Define Cost/Loss Function to Evaluate the Model)

在定义了带有未知参数的模型之后，我们需要一种方法来衡量模型的预测结果与真实目标值之间的差异。这个衡量标准就是代价函数 (Cost Function) 或 损失函数 (Loss Function)。

我们可以从一个通用的角度来形式化地定义这个概念：

1. 给定一个数据集 (Given a dataset D):
   我们的训练数据是一个包含 N 个样本的集合 D：

   $$D=\{(x^1,{\hat{y}}^1),(x^2,{\hat{y}}^2),\dots ,(x^N,{\hat{y}}^N)\}$$

   其中，$x^n$ 是第 n 个样本的输入特征（例如，一张宝可梦的图片），${\hat{y}}^n$ 是该样本对应的真实标签或目标值（例如，“拉达”）。
   (注：在此处以及李宏毅老师的课程中，$\hat{y}$ 常用来表示真实的、作为“帽子”或目标的标签。在其他文献中，$\hat{y}$ 也常用来表示模型的预测值。请根据上下文区分。)

2. 定义函数的总损失 (Define the Total Loss of a Function):
   对于一个我们想要评估的函数（或模型、假设）$h$，它在整个数据集 $D$ 上的总损失 $L(h,D)$，通常定义为所有单个样本损失的平均值。

   $$L(h,D)=\frac{1}{N}\sum _{n=1}^{N}l(h,x^n,{\hat{y}}^n)$$

   这里，$l(h,x^n,{\hat{y}}^n)$ 是函数 $h$ 在单个样本 $(x^n,{\hat{y}}^n)$ 上的损失。它衡量了模型在该样本上的预测（即 $h(x^n)$）与真实标签 ${\hat{y}}^n$ 之间的差距。

现在，我们将这个通用框架应用到我们具体的参数化模型上。我们的“函数” $h$ 是由未知参数（如 $w$ 和 $b$）定义的。因此，衡量函数好坏的总损失，实际上就成了衡量这组参数好坏的指标。

代价函数是参数的函数 (Loss is a function of parameters):
给定训练数据集，对于一组特定的模型参数（例如 $w$ 和 $b$），我们可以计算出模型在整个训练集上的总体表现。因此，代价函数 $L$ 可以看作是这些未知参数的函数。例如，对于参数 $w$ 和 $b$，代价函数可以表示为 $L(w,b)$。

这里：

• $N$ 是训练样本的总数。
• $e_n$ 对应于上面通用定义中的单个样本损失 $l(\cdot )$，即模型在第 $n$ 个训练样本上的误差 (error) 或 损失 (loss)。
• 代价函数 $L(w,b)$ 是所有单个样本损失的平均值（或总和）。

常见的单个样本损失计算方式 ($e_n$):

• 平均绝对误差 (Mean Absolute Error, MAE):$$e_n=|{\hat{y}}^{(n)}-y^{(n)}|$$
• 均方误差 (Mean Squared Error, MSE):$$e_n=({\hat{y}}^{(n)}-y^{(n)}{)}^2$$
• 交叉熵 (Cross-Entropy):
  常用于分类问题，衡量预测概率分布与真实类别分布之间的差异。具体形式取决于二分类还是多分类。
  • 二分类交叉熵 (Binary Cross-Entropy):
    $e_n=-[y^{(n)}\log ({\hat{y}}^{(n)})+(1-y^{(n)})\log (1-{\hat{y}}^{(n)})]$
    (其中 $y^{(n)}\in \{0,1\}$, ${\hat{y}}^{(n)}$ 是预测为类别1的概率)
  • 多分类交叉熵 (Categorical Cross-Entropy):
    $e_n=-\sum _{k=1}^K{y}_k^{(n)}\log ({\hat{y}}_k^{(n)})$
    (其中 $y^{(n)}$ 是one-hot编码的真实标签, ${\hat{y}}^{(n)}$ 是预测的概率分布, $K$ 是类别数)

损失函数的作用 (The Role of the Loss Function):
损失函数告诉我们当前这组参数 $(w,b)$ 的表现有多好 (how good a set of values is)。我们的目标是找到一组参数，使得这个损失函数的值最小。

误差平面 (Error Surface):
我们可以将损失函数 $L(w,b)$ 想象成一个多维空间中的曲面，其中参数（如 $w$ 和 $b$）是坐标轴，损失函数的值是高度。这个曲面被称为误差平面 (Error Surface) 或损失平面。
(图示：损失值如何随着参数变化而变化，目标是找到曲面的最低点)

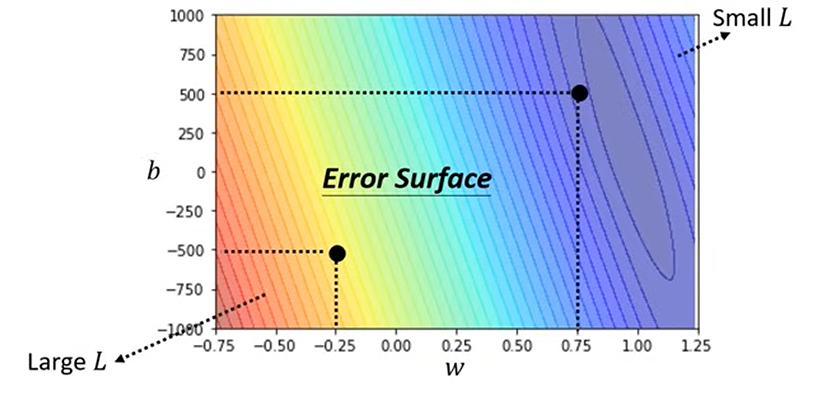
1.2.3 学习的目标：泛化 (The Goal of Learning: Generalization)

一旦我们定义了模型和损失函数 $L(w,b)$，接下来的目标就是找到一组最优的参数 $w^{\ast }$ 和 $b^{\ast }$，使得损失函数的值最小。这个过程称为优化 (Optimization)。

但在我们深入探讨如何进行优化（例如使用梯度下降）之前，一个根本性的问题值得思考：我们为什么相信，在一个有限的训练数据集上最小化损失，能帮助我们找到一个在所有未见过的真实数据上都表现良好的模型呢？ 毕竟，我们真正关心的是模型在未来遇到新数据时的表现，而不是它在已经看过的训练数据上的表现。

这个问题引出了机器学习的核心目标：泛化 (Generalization)。

这张图片从理论上解释了我们想要达成的目标以及如何实现它。让我们来分解一下其中的符号：

• ${\mathcal{D}}_{all}$: 代表所有可能的数据的集合，它遵循真实的数据分布。这是理论上的概念，我们永远无法完全获得它。
• ${\mathcal{D}}_{train}$: 我们实际拥有的训练数据集，它是从 ${\mathcal{D}}_{all}$ 中抽取的一个样本。
• $\mathcal{H}$: 假设空间 (Hypothesis Space)，即我们模型能表示的所有可能的函数的集合。
• $h^{all}=\arg \underset{h\in \mathcal{H}}{min}L(h,{\mathcal{D}}_{all})$: 理论上最优的模型。这个模型是在所有数据上能达到的最低损失，是我们的“上帝视角”下的完美答案。我们无法直接得到它。
• $h^{train}=\arg \underset{h\in \mathcal{H}}{min}L(h,{\mathcal{D}}_{train})$: 我们在训练集上找到的最优模型。这是我们通过优化算法（如梯度下降）实际得到的模型。

我们真正想要什么？(What do we want?)

我们最终的目标是：

• $L(h^{train},{\mathcal{D}}_{all})$: 这是我们实际得到的模型 ($h^{train}$) 在所有真实数据上的损失。这代表了我们模型的真实泛化能力。
• $L(h^{all},{\mathcal{D}}_{all})$: 这是理论上最优模型 ($h^{all}$) 在所有真实数据上的损失。这是我们能达到的理论最低损失。

这整个公式的含义是：我们希望，我们训练出的模型 ($h^{train}$) 的真实表现，与理论上最好的模型 ($h^{all}$) 的表现之间的差距（即泛化差距, Generalization Gap）能够尽可能小（小于一个很小的数 $\delta$）。

如何才能实现这个目标？

我们无法直接计算 $L(h,{\mathcal{D}}_{all})$。那么，我们需要对我们的训练集 ${\mathcal{D}}_{train}$ 提出什么样的要求，才能间接地保证上述目标呢？

答案是：我们的训练集 ${\mathcal{D}}_{train}$ 必须对 ${\mathcal{D}}_{all}$ 有足够的代表性。

数学上，这个“代表性”可以表示为一个更强的条件：

这个条件的意思是：对于我们考虑的任何一个可能的模型 $h$，它在训练集上的损失 $L(h,{\mathcal{D}}_{train})$ 都应该非常接近它在所有数据上的真实损失 $L(h,{\mathcal{D}}_{all})$。换句话说，训练损失是真实损失的一个很好的估计。

推导过程：

如果上述“代表性”条件成立，我们就可以推导出我们想要的目标：

1. $L(h^{train},{\mathcal{D}}_{all})$

   • 我们从我们模型的真实损失开始。

2. $\le L(h^{train},{\mathcal{D}}_{train})+\delta /2$

   • 根据“代表性”条件，对于 $h^{train}$ 而言，它的真实损失不会比它的训练损失大太多。

3. $\le L(h^{all},{\mathcal{D}}_{train})+\delta /2$

   • 这是关键一步。根据 $h^{train}$ 的定义，它是在训练集 ${\mathcal{D}}_{train}$ 上使得损失最小的模型。因此，它的训练损失 $L(h^{train},{\mathcal{D}}_{train})$ 必然小于或等于任何其他模型在训练集上的损失，当然也包括 $h^{all}$ 的训练损失 $L(h^{all},{\mathcal{D}}_{train})$。

4. $\le L(h^{all},{\mathcal{D}}_{all})+\delta /2+\delta /2$

   • 再次使用“代表性”条件，这次是对于 $h^{all}$。它的训练损失不会比它的真实损失大太多。

5. $=L(h^{all},{\mathcal{D}}_{all})+\delta$

   • 整理一下，我们就得到了最终的不等式。

结论:
这个推导告诉我们一个深刻的道理：只要我们的训练数据能够很好地代表整体数据分布，那么通过最小化训练集上的损失（这个过程也叫经验风险最小化, Empirical Risk Minimization, ERM），我们就有理论保证能找到一个泛化能力接近理论最优的模型。

但这引出了下一个关键问题：我们如何保证我们拿到的训练集 ${\mathcal{D}}_{train}$ 就是有代表性的，而不是一个“坏”的、有偏见的数据集呢？这就涉及到对失败概率的分析。

1.2.4 失败的概率 (Probability of Failure)

让我们更深入地探讨“坏”数据集的概念。一个训练集 ${\mathcal{D}}_{train}$ 被认为是“坏”的，如果它不满足我们之前提到的“代表性”条件。也就是说，存在至少一个我们可能考虑的模型 $h$，使得这个模型在 ${\mathcal{D}}_{train}$ 上的表现与它在真实世界 ${\mathcal{D}}_{all}$ 上的表现差异巨大。

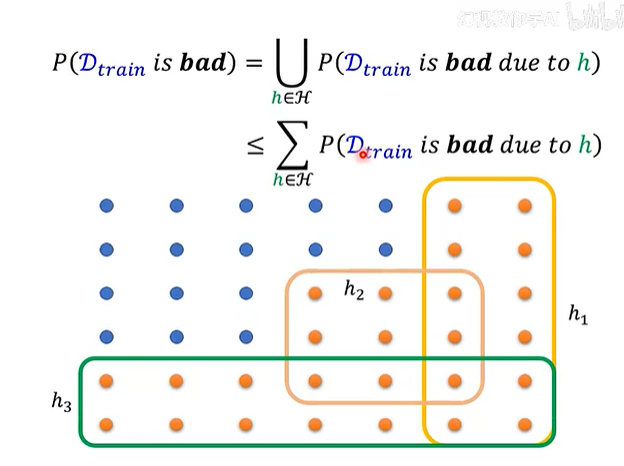
这张图和公式从数学上分解了“坏”的概率。

1. 将“坏”分解 (Decomposing "Bad")

• $P({\mathcal{D}}_{train}\text{ is bad due to }h)$: 这代表一个更具体的失败事件。它指的是，我们抽到的训练集 ${\mathcal{D}}_{train}$ 恰好对某一个特定的模型 $h$ 产生了误导。

  • 例如，在图中的橙色区域，h₁（黄色框）圈出了一些训练集。对于这些训练集来说，模型h₁在它们上面的表现（训练损失）看起来很好，但其实h₁在真实世界中的表现很差。这些训练集对h₁来说是“坏”的。
  • 同理，h₂（粉色框）和h₃（绿色框）也各自有一批对它们自己而言是“坏”的训练集。

• $P({\mathcal{D}}_{train}\text{ is bad})=\bigcup _{h\in \mathcal{H}}P({\mathcal{D}}_{train}\text{ is bad due to }h)$

  • 这个公式说明，我们整体的训练过程会失败（即我们抽到的 ${\mathcal{D}}_{train}$ 是“坏”的），当且仅当这个 ${\mathcal{D}}_{train}$ 至少对我们模型库 $\mathcal{H}$ 中的某一个模型 $h$ 产生了误导。
  • 在图中，所有橙色点（坏的训练集）的集合，就是h₁的坏集、h₂的坏集、h₃的坏集...等等所有可能模型的坏集的并集 (Union, ∪)。

2. 使用联合界进行放缩 (Using the Union Bound)

直接计算并集的概率通常很复杂。因此，我们使用一个在概率论中常用的技巧——联合界 (Union Bound) 或布尔不等式 (Boole's Inequality)——来放缩它。

这个不等式告诉我们，总的失败概率不会超过所有单个失败事件概率的总和 (Sum, Σ)。如果我们能证明这个总和很小，那么总的失败概率就一定更小。

3. 霍夫丁不等式 (Hoeffding's Inequality)

现在，我们需要一个工具来计算单个失败事件的概率 $P({\mathcal{D}}_{train}\text{ is bad due to }h)$。霍夫丁不等式正是完成这个任务的强大工具。

它告诉我们，对于任何一个固定的模型 $h$，其在训练集上的损失与在真实世界上的损失之差大于某个值 $ϵ$ 的概率，有一个指数级的上界：

• $N$ 是训练集 ${\mathcal{D}}_{train}$ 的大小。
• $ϵ$ 是我们能容忍的误差界限。
• 这个公式清晰地表明，随着训练集大小 $N$ 的增加，单个模型 $h$ 被误判的概率会指数级地减小。

4. 综合结论

将联合界和霍夫丁不等式结合起来，我们就得到了一个关于总失败概率的上界：

如果我们的模型库 $\mathcal{H}$ 是有限的（包含 $M$ 个模型），那么：

这个最终的公式为我们的信念提供了坚实的数学支撑：只要我们的训练集 $N$ 足够大，即使考虑到所有可能的模型，我们不幸抽到一个“坏”的、不具代表性的训练集的概率也会趋近于零。

为什么使用了验证集后，模型依然可能过拟合？ (Why may the model still overfit after using the validation set)

(注：对于神经网络这种模型库 $\mathcal{H}$ 包含无限个函数的情况，需要更高级的理论如 VC 维 (VC Dimension) 来处理，但其核心思想与此类似。)

但是，这个结论中隐藏着一个微妙的矛盾，这引出了关于模型选择的核心问题。

1.2.5 模型复杂度的权衡 (Tradeoff of Model Complexity)

让我们再回顾一下泛化差距的保证：我们希望 $L(h^{train},{\mathcal{D}}_{all})-L(h^{all},{\mathcal{D}}_{all})\le \delta$。
根据之前的推导，为了让这个差距 $\delta$ 变小，我们需要：

• 更大的训练集 $N$ (Larger N)
• 更小的模型库 $|\mathcal{H}|$ (smaller |H|)
  和霍夫丁不等式相关的过拟合原因 (The reasons for overfitting related to Hofding's inequality)
  然而，这两个目标，特别是对模型库 $|\mathcal{H}|$ 的要求，引发了一个深刻的权衡。

两个相互冲突的目标

1. 目标一：小的泛化差距 (Small Generalization Gap)

   • 为了让 $L(h^{train},{\mathcal{D}}_{all})$ 接近 $L(h^{all},{\mathcal{D}}_{all})$，即我们训练出的模型接近理论最优模型，我们需要一个更小的模型库 $|\mathcal{H}|$。
   • 原因：模型库越小（模型越简单），过拟合的风险就越小，从有限数据中学到的规律就越可能适用于真实世界。

2. 目标二：小的理论最低损失 (Small Theoretical Minimum Loss)

   • 我们不仅希望 $h^{train}$ 接近 $h^{all}$，我们还希望 $h^{all}$ 本身就很强，即 $L(h^{all},{\mathcal{D}}_{all})$ 这个值本身要很小。
   • 要实现这一点，我们需要一个更大的模型库 $|\mathcal{H}|$。
   • 原因：一个更大的模型库（比如一个更深、更宽的神经网络）意味着我们的模型表达能力更强，能够拟合更复杂的数据关系。一个简单的线性模型库可能永远无法很好地解决复杂的图像识别问题，它的 $L(h^{all},{\mathcal{D}}_{all})$ 本身就会很大。

图解权衡 (Interpreting the Diagram)

这张图非常直观地展示了这个矛盾：

• 左图：大的模型库 (larger |H|)

  • 优点: 因为模型库非常强大，它包含了非常复杂的函数。因此，理论上最好的模型 $h^{all}$ 能够完美地拟合所有真实数据，其损失 $L(h^{all},{\mathcal{D}}_{all})$ 非常小 (small)。
  • 缺点: 正因为模型库太大了，我们在有限的训练集上找到的 $h^{train}$ 很容易过拟合。它在真实世界中的表现 $L(h^{train},{\mathcal{D}}_{all})$ 会很差，导致 $h^{train}$ 和 $h^{all}$ 之间的差距非常大 (large)。

• 右图：小的模型库 (smaller |H|)

  • 优点: 因为模型库很简单，过拟合的风险很低。我们在训练集上找到的 $h^{train}$ 的真实表现 $L(h^{train},{\mathcal{D}}_{all})$ 会非常接近理论最优 $h^{all}$ 的表现。它们之间的差距很小 (small)。
  • 缺点: 模型库本身太弱了（“先天不足”），即使是其中最好的模型 $h^{all}$，也无法很好地拟合真实数据。因此，理论最低损失 $L(h^{all},{\mathcal{D}}_{all})$ 本身就非常大 (large)。

鱼与熊掌可以兼得吗？(Can we have the fish and the bear's paw?)

这个问题的答案是“不可以”，这就是机器学习中的“没有免费的午餐”定理的一个体现。我们必须在两者之间做出选择和权衡。

• 模型过于简单 (高偏差, High Bias): 对应右图。模型无法捕捉数据的真实规律，导致在训练集和测试集上表现都很差。
• 模型过于复杂 (高方差, High Variance): 对应左图。模型过度学习了训练集中的噪声和细节，导致在训练集上表现很好，但在测试集上表现很差（泛化能力差）。

实际操作中的意义:
我们的目标是找到一个复杂度适中的模型，使得 $L(h^{train},{\mathcal{D}}_{all})$ 这个最终的、我们真正关心的损失值达到最小。这通常意味着：

1. 选择一个足够强大的模型库（比如一个深度神经网络），以确保 $L(h^{all},{\mathcal{D}}_{all})$ 足够小。
2. 同时使用大量的训练数据 ($N$) 和各种正则化 (Regularization) 技术（如权重衰减、Dropout等），来有效地减小泛化差距，防止过拟合。

理解这个权衡是设计和调试机器学习模型的关键。它指导我们如何根据问题的复杂度和可用数据量来选择合适的模型架构和训练策略。

1.2.6 参数优化 (Optimization)

霍夫丁不等式和上面的公式从理论上保证了，我们接下来要做的“参数优化”——在训练集上寻找最优模型——是一件有意义且大概率会成功的事情。

数学上，我们可以表示为：

这意味着我们要寻找使损失函数 $L$ 达到最小值的参数 $w$ 和 $b$。

主要方法：梯度下降 (Ways: Gradient Descent)
梯度下降是一种广泛应用于机器学习和深度学习中的迭代优化算法，用于寻找函数的最小值。其基本思想是沿着损失函数梯度下降最快的方向逐步调整参数。

梯度下降的步骤:

1. 初始化参数 (Pick an initial value):
   随机选择或根据某种策略设定参数的初始值，例如 $w^0,b^0$。

2. 计算梯度 (Compute Gradient):
   计算损失函数 $L$ 在当前参数点（例如 $w^t,b^t$）关于每个参数的偏导数（即梯度）。

   • 对于参数 $w$: $\frac{\partial L}{\partial w}{|}_{w=w^t,b=b^t}$
   • 对于参数 $b$: $\frac{\partial L}{\partial b}{|}_{w=w^t,b=b^t}$
     梯度指明了在该点函数值增长最快的方向。

3. 确定更新量 (Determine Update Amount):

   • $\eta$ (eta) 代表学习率 (Learning Rate)，它是一个超参数 (Hyperparameters)，控制每次参数更新的步长。
   • 参数更新的量由学习率乘以梯度的负值决定（因为我们要向梯度反方向，即下降方向移动）：
     • 对 $w$ 的更新量: $-\eta \frac{\partial L}{\partial w}{|}_{w=w^t,b=b^t}$
     • 对 $b$ 的更新量: $-\eta \frac{\partial L}{\partial b}{|}_{w=w^t,b=b^t}$

4. 更新参数 (Update Parameters):
   将当前参数值减去上一步计算的更新量，得到新的参数值：

   $$w^{t+1}=w^t-\eta \frac{\partial L}{\partial w}{|}_{w=w^t,b=b^t}$$$$b^{t+1}=b^t-\eta \frac{\partial L}{\partial b}{|}_{w=w^t,b=b^t}$$

5. 迭代 (Update iteratively):
   重复步骤 2 到 4，直到损失函数收敛到足够小的值，或者达到预设的最大迭代次数，或者满足其他停止条件。

梯度下降的直观理解: 想象你在一个山上（误差平面），目标是走到山谷的最低点。在每一步，你都会观察当前位置哪个方向坡度最陡峭向下（梯度的反方向），然后朝着那个方向走一小步（步长由学习率控制）。

1.2.7 机器学习核心步骤与深度学习的关系 (Relationship of Core Machine Learning Steps to Deep Learning)

上述三个核心步骤——1. 定义一个带有未知参数的模型，2. 定义一个损失函数来评估模型，以及 3. 通过优化算法寻找最优参数——构成了监督式机器学习的完整流程，并且这一框架在深度学习中得到了直接的应用和显著的扩展：

1. 参数化模型的核心思想一致 (Consistent Core Idea of Parameterized Models):

   • 无论是简单的线性回归还是复杂的深度神经网络，其本质都是参数化的函数/模型，包含大量需要从数据中学习的未知参数（权重和偏置）。
   • 深度学习模型（如神经网络）通过多层非线性变换构建出表达能力极强的参数化函数。

2. 损失函数作为统一的评估和优化目标 (Loss Function as a Unified Goal for Evaluation and Optimization):

   • 对于任何参数化模型，都需要一个损失函数来量化其预测与真实目标之间的差距。
   • 在深度学习中，训练的目标同样是找到一组使损失函数最小化的参数。

3. 优化算法作为学习的驱动力 (Optimization Algorithms as the Engine of Learning):

   • 梯度下降及其变体是深度学习中最核心的优化工具。由于深度神经网络参数众多，损失函数的“误差平面”异常复杂，包含许多局部最小值、鞍点等。
   • 深度学习领域发展了许多先进的梯度下降变体，如：
     • 随机梯度下降 (Stochastic Gradient Descent, SGD): 每次使用单个样本计算梯度并更新，速度快但波动大。
     • Mini-batch 梯度下降: 每次使用一小批样本计算梯度，是 Batch GD 和 SGD 的折衷，也是目前最常用的方法。
     • 带动量的优化器 (Optimizers with Momentum): 如 Momentum, Nesterov Accelerated Gradient (NAG)，通过引入动量项加速收敛并帮助越过小的局部极值点。
     • 自适应学习率优化器 (Adaptive Learning Rate Optimizers): 如 AdaGrad, RMSProp, Adam, AdamW，它们能为每个参数自动调整学习率，通常能更快收敛且对初始学习率不那么敏感。
   • 反向传播 (Backpropagation): 对于深度神经网络这样复杂的复合函数，高效计算梯度至关重要。反向传播算法利用链式法则，系统地计算损失函数关于网络中所有参数的梯度，为梯度下降提供“方向盘”。

4. 深度学习的扩展与深化 (Extensions and Deepening in Deep Learning):

   • 模型复杂度与层级结构: 深度学习通过构建深层网络结构极大地扩展了模型的复杂度，使其能够学习从低级到高级的层次化特征表示。
   • 非线性能力: 深度学习模型广泛使用非线性激活函数，使其能够学习高度非线性的映射关系。
   • 特定任务的损失与模型: 针对各种复杂任务（图像识别、自然语言处理等），深度学习发展了特定的网络架构（如CNNs, RNNs, Transformers）和相应的损失函数。
   • 端到端学习 (End-to-End Learning): 深度学习常常实现“端到端”学习，即从原始输入直接学习到最终输出，整个过程由参数通过最小化损失函数自动学习得到。

总结来说，"定义模型"、"定义损失函数" 和 "优化参数" 这三个步骤是机器学习（尤其是监督学习）的基本骨架。深度学习在这个骨架的基础上，通过构建更复杂强大的模型（神经网络）、采用合适的损失函数，并利用高效的优化算法（如基于反向传播的梯度下降及其变体），来解决更具挑战性的问题并取得了巨大成功。理解这三个基本步骤及其在深度学习中的具体实现，是掌握深度学习原理的关键。

2. 深度学习基本概念 (Basic Concepts of Deep Learning)

Video: https://www.youtube.com/watch?v=bHcJCp2Fyxs

2.1 步骤一：定义带有未知参数的函数/模型 (Step 1: Define a Function/Model with Unknown Parameters)

2.1.1 动机：线性模型的局限性 (Model Bias of Linear Models)

线性模型，如 $y=b+w{x}_1$ 或 $y=b+\sum _j{w}_j{x}_j$，在许多情况下非常有用且易于解释。然而，它们具有固有的模型偏差 (Model Bias)，这意味着它们只能表示输入和输出之间的线性关系。

• 局限性 (Limitation): 如果数据中的真实关系是非线性的，线性模型将无法很好地拟合数据，导致预测性能不佳。
  • 例如，在你的图示中（第一张图，红色曲线），如果 $y$ 和 $x_1$ 之间的关系是如图所示的折线，那么单一的直线（线性模型）无法准确地捕捉这种模式。

2.1.2 构建更灵活的模型：分段线性函数 (Building More Flexible Models: Piecewise Linear Functions)

为了克服线性模型的局限性，我们需要能够表示非线性关系的更灵活的模型。一种方法是使用分段线性函数 (Piecewise Linear Curves)。

• 基本思想 (Core Idea): 任何复杂的分段线性曲线（如图中的红色曲线）可以被看作是一个常数 (constant) 加上一系列更简单的“阶梯状”或“斜坡状”基础函数（如图中右上角示意的小蓝色函数）的加权和 (sum of a set of blue functions)。
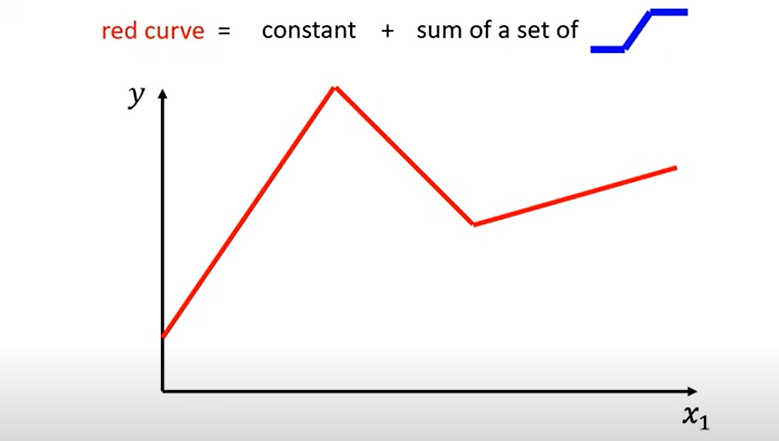
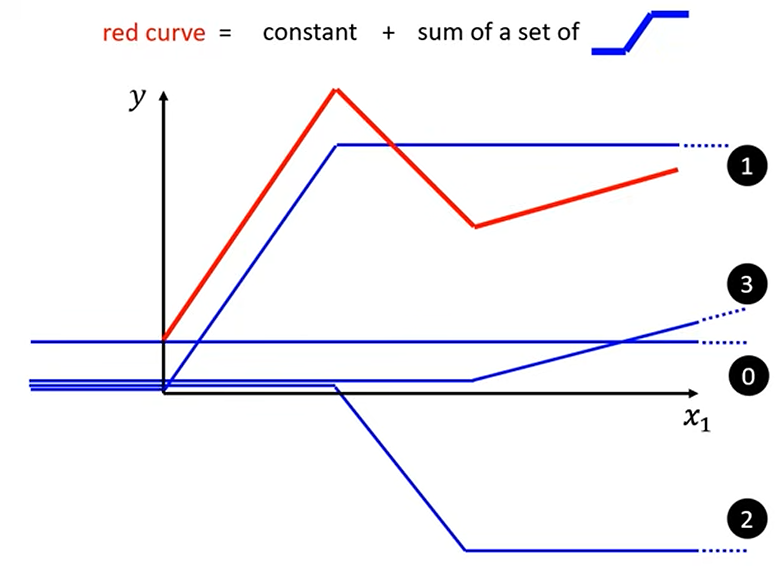
  第一张图展示了一个目标分段线性函数（红色曲线）。
  第二张图展示了如何将这个红色曲线分解为多个基础的蓝色函数。
  每个蓝色函数在某个点改变其斜率。

• 逼近任意连续曲线 (Approximating Arbitrary Continuous Curves):

  • 即使目标函数不是严格的分段线性函数，我们也可以通过在其上选择足够多的点，并用连接这些点的折线（即分段线性函数）来近似它。
  • 关键: 要想获得好的近似效果，我们需要足够多的“片段”(pieces) 或基础蓝色函数。

• 如何表示基础的“蓝色函数” (How to represent the blue function / Hard Sigmoid)?

  • 这种在某个点改变斜率，从平坦变为有斜率再变为平坦的基础函数，可以被称为硬 Sigmoid (Hard Sigmoid) 或斜坡函数。
  • 更进一步，我们可以使用平滑的 Sigmoid 函数来近似这种硬 Sigmoid 的行为，或者直接用 Sigmoid 函数作为构建块。标准的 Sigmoid 函数定义为：$$\text{sigmoid}(z)=\frac{1}{1+e^{-z}}$$
  • 通过调整 Sigmoid 函数的参数，我们可以控制这个“平滑阶梯”的形状：
    • 考虑一个经过缩放和平移的 Sigmoid 函数： $y=c\cdot \text{sigmoid}(b^{\prime }+w^{\prime }{x}_1)$ (这里为了与你笔记中的 $b_i,w_i$ 对应，我们暂时用 $b^{\prime },w^{\prime }$)
    • $w^{\prime }$ (权重, weight): 改变 Sigmoid 函数的斜率 (slope) 或陡峭程度。
    • $b^{\prime }$ (偏置, bias): 改变 Sigmoid 函数在 $x_1$ 轴上的平移 (shift) 位置。
    • $c$ (系数, coefficient): 改变 Sigmoid 函数的高度 (height) 或幅度。

• 用 Sigmoid 函数构建分段线性模型 (Building Piecewise Linear Models with Sigmoid Functions):

  • 因此，原始的目标分段线性函数 $y$ (或其近似) 可以被表示为一系列 Sigmoid 函数的加权和，再加上一个整体的偏置：

    $$y=b_{overall}+\sum _i{c}_i\cdot \text{sigmoid}(b_i+w_i{x}_1)$$

    这里：

    • $b_{overall}$ 是整体的偏置项 (constant)。
    • $c_i,b_i,w_i$ 分别是第 $i$ 个 Sigmoid 组件的高度、平移和斜率控制参数。
    • 每个 $c_i\cdot \text{sigmoid}(b_i+w_i{x}_1)$ 就对应于一个“蓝色函数”组件。

  • 其他激活函数 (Other Activation Functions) - 例如 ReLU:
    除了 Sigmoid 函数，还有许多其他的激活函数 (Activation Functions) 可以用来在神经网络中引入非线性，从而构建能够拟合复杂模式的模型。

    • ReLU (Rectified Linear Unit) 是目前深度学习中最常用的一种激活函数。其定义为：$$\text{ReLU}(z)=max(0,z)$$
    • 如果使用 ReLU 作为激活函数，并且考虑到多特征输入（即每个 ReLU 单元的输入是 $\sum _j{w}_{ij}{x}_j+b_i$），那么模型可以表示为：$$y=b_{output}+\sum _i{c}_i\cdot \text{ReLU}(b_{hidden,i}+\sum _j{w}_{ij}{x}_j)$$或者更简洁地写成：$$y=b_{output}+\sum _i{c}_i\cdot max(0,b_{hidden,i}+\sum _j{w}_{ij}{x}_j)$$
    • 为什么 ReLU 常用？
      • 计算简单高效: ReLU 的计算非常快（只是一个取最大值的操作）。
      • 缓解梯度消失问题: 对于正输入，ReLU 的梯度是1，这有助于在深层网络中更好地传播梯度，缓解了 Sigmoid 等函数在输入值很大或很小时梯度接近0（梯度消失）的问题。
      • 稀疏性: ReLU 会使一部分神经元的输出为0（当输入为负时），这可以带来一定的网络稀疏性，有时被认为有助于特征学习。
    • 当然，ReLU 也有其缺点，比如“Dying ReLU”问题（神经元可能永久失活）。

  • 激活函数的角色: 深度学习 (Deep Learning)#^c0241b
    无论是 Sigmoid, ReLU, Tanh 还是其他激活函数，它们的核心作用都是在神经网络的每一层（或特定层）引入非线性，使得网络能够学习和表示输入与输出之间复杂的、非线性的映射关系。没有非线性激活函数，多层神经网络将退化为一个等效的单层线性模型。

  • 哪个更好 (Which is better)?

    • 激活函数的选择取决于具体的应用场景、网络结构和经验。
    • 在许多现代深度学习应用中，ReLU 及其变体 (如 Leaky ReLU, PReLU, ELU 等) 通常是隐藏层的首选激活函数，因为它们往往能带来更好的训练动态和性能。
    • Sigmoid 和 Tanh 仍然在某些特定场景下使用，例如 Sigmoid 常用于二分类问题的输出层（输出概率），Tanh 有时用于隐藏层（其输出范围在-1到1之间，中心对称）。

2.1.3 推广到多特征输入：构建神经网络模型 (Generalizing to Multiple Features: Building a Neural Network Model)

上面的讨论是基于单个输入特征 $x_1$。现在，我们将这个思想推广到具有多个输入特征 $x_j$ 的情况。

• 从简单线性模型到 Sigmoid 组合 (From Simple Linear Model to Sigmoid Combination):

  • 对于单特征:$$y=b+w{x}_1\Rightarrow y=b_{overall}+\sum _i{c}_i\cdot \text{sigmoid}(b_i+w_i{x}_1)$$
  • 对于多特征，线性模型为: $y=b+\sum _j{w}_j{x}_j$
  • 类比地，我们将每个 Sigmoid 函数的输入从 $b_i+w_i{x}_1$ 推广为多个特征的线性组合 $b_i+\sum _j{w}_{ij}{x}_j$:$$y=b_{overall}+\sum _i{c}_i\cdot \text{sigmoid}(b_i+\sum _j{w}_{ij}{x}_j)$$

• 引入神经网络的表示方法 (Introducing Neural Network Notation):
  让我们用更标准的神经网络符号来重写这个模型。

  • 第一步：计算每个 Sigmoid 的输入 (通常称为加权输入或 pre-activation)
    对于第 $i$ 个 Sigmoid 组件（可以看作是隐藏层的一个神经元），其输入 $r_i$ 是所有输入特征 $x_j$ 的加权和，再加上该组件的偏置 $b_i$:

    $$r_i=b_i+\sum _j{w}_{ij}{x}_j$$

    其中 $w_{ij}$ 是连接第 $j$ 个输入特征 $x_j$ 到第 $i$ 个 Sigmoid 组件的权重。

    • 矩阵形式 (Vectorized Form):
      如果我们将所有输入特征表示为向量 $x=[x_1,x_2,\dots ,x_N{]}^T$，所有偏置 $b_i$ 组成向量 $\mathbf{b}=[b_1,b_2,\dots ,b_M{]}^T$，所有权重 $w_{ij}$ 组成权重矩阵 $W$ (其中 $W_{ij}$ 是 $w_{ij}$)，那么所有 $r_i$ 组成的向量 $\mathbf{r}=[r_1,r_2,\dots ,r_M{]}^T$ 可以表示为：$$\mathbf{r}=\mathbf{b}+W\mathbf{x}$$即：$$\left(\begin{array}{c}{r}_1^{(j+1)}\\ r_2^{(j+1)}\\ ⋮\\ r_{N_{j+1}}^{(j+1)}\end{array}\right)=\left(\begin{array}{c}{b}_1^{(j+1)}\\ b_2^{(j+1)}\\ ⋮\\ b_{N_{j+1}}^{(j+1)}\end{array}\right)+\left(\begin{array}{cccc}{W}_{1,1}^{(j+1)}& W_{1,2}^{(j+1)}& \cdots & W_{1,N_j}^{(j+1)}\\ W_{2,1}^{(j+1)}& W_{2,2}^{(j+1)}& \cdots & W_{2,N_j}^{(j+1)}\\ ⋮& ⋮& \ddots & ⋮\\ W_{N_{j+1},1}^{(j+1)}& W_{N_{j+1},2}^{(j+1)}& \cdots & W_{N_{j+1},N_j}^{(j+1)}\end{array}\right)\left(\begin{array}{c}{a}_1^{(j)}\\ a_2^{(j)}\\ ⋮\\ a_{N_j}^{(j)}\end{array}\right)$$

  • 第二步：应用 Sigmoid 激活函数 (Apply Sigmoid Activation Function)
    将每个 $r_i$ 通过 Sigmoid 函数得到激活值 $a_i$：

    $$a_i=\text{sigmoid}(r_i)$$
    • 矩阵形式 (Vectorized Form):
      如果 $\sigma (\cdot )$ 表示逐元素应用 Sigmoid 函数，那么激活向量 $\mathbf{a}=[a_1,a_2,\dots ,a_M{]}^T$ 可以表示为：$$\mathbf{a}=\sigma (\mathbf{r})=\sigma (\mathbf{b}+W\mathbf{x})$$

    这些激活值 $a_i$ 构成了神经网络的隐藏层 (Hidden Layer) 的输出。

  • **第三步：组合隐藏层输出得到最终预测 (Combine Hidden Layer Outputs for Final Prediction)
    最终的输出 $y$ 是这些隐藏层激活值 $a_i$ 的加权和，再加上一个最终的输出层偏置 $b_{output}$ (对应图 7.png 中的 $b$)。权重为 $c_i$。

    $$y=b_{output}+\sum _i{c}_i{a}_i$$
    • 矩阵形式 (Vectorized Form):
      如果我们将权重 $c_i$ 组成一个行向量 ${\mathbf{c}}^T=[c_1,c_2,\dots ,c_M]$ (或者列向量 $\mathbf{c}$ 然后取转置)，则：$$y=b_{output}+{\mathbf{c}}^T\mathbf{a}$$

  • 整合模型 (Putting It All Together):
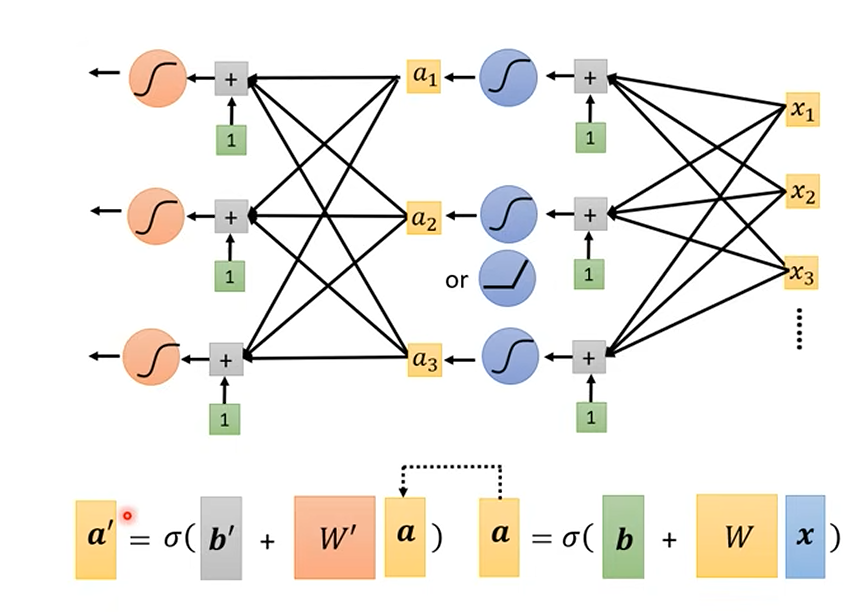
    将以上步骤整合，我们就得到了一个具有单隐藏层的神经网络模型：

    $$y=b_{output}+{\mathbf{c}}^T\sigma ({\mathbf{b}}_{hidden}+W\mathbf{x})$$

    这里：

    • $\mathbf{x}$ 是输入特征向量。
    • $W$ 是输入层到隐藏层的权重矩阵。
    • ${\mathbf{b}}_{hidden}$ 是隐藏层的偏置向量。
    • $\sigma (\cdot )$ 是 Sigmoid 激活函数（或其他非线性激活函数）。
    • ${\mathbf{c}}^T$ 是隐藏层到输出层的权重向量。
    • $b_{output}$ 是输出层的偏置。
    • 所有 $W,{\mathbf{b}}_{hidden},{\mathbf{c}}^T,b_{output}$ 都是模型需要从数据中学习的未知参数。

  • 
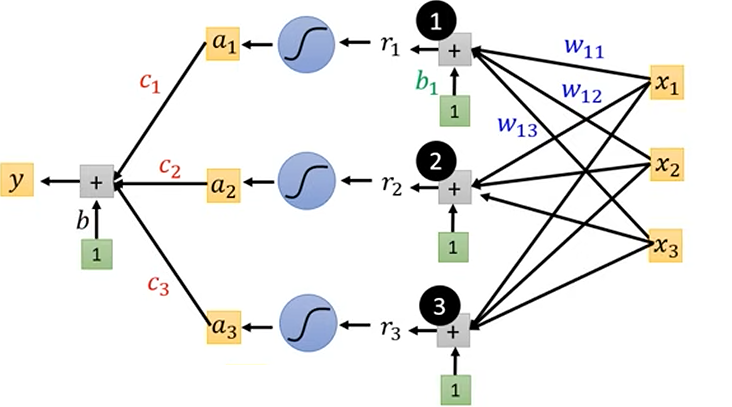
    这张图完美地展示了这个单隐藏层神经网络的结构：

    • 输入层 (Input Layer): $x_1,x_2,x_3$。
    • 隐藏层 (Hidden Layer):
      • 三个神经元（用黑色圆圈1, 2, 3表示）。
      • 每个神经元首先计算加权输入 $r_i=b_i+\sum _j{w}_{ij}{x}_j$ (图中 $b_1,b_2,b_3$ 是隐藏层偏置，通过连接值为1的绿色方块引入；$w_{11},w_{12},\dots$ 是权重)。
      • 然后通过 Sigmoid 激活函数（蓝色弯曲符号）得到激活值 $a_1,a_2,a_3$。
    • 输出层 (Output Layer):
      • 计算 $y=b+c_1{a}_1+c_2{a}_2+c_3{a}_3$ (图中 $b$ 是输出层偏置，通过连接值为1的绿色方块引入；$c_1,c_2,c_3$ 是隐藏层到输出层的权重)。

• 随机性: 当我们刚开始训练一个神经网络时，我们并不知道参数 $w,b,c$ (以及更复杂的网络中的所有权重和偏置) 应该是什么值。
• 因此，我们通常会用小的随机数来初始化这些参数。比如，从一个均值为0，方差很小的高斯分布中采样，或者在一个小的区间内均匀采样

• 所以最初，表达式 $c_i\cdot \text{sigmoid}(b_i+w_i{x}_1)$ （以及整个模型）是一个包含未知参数的函数模板或函数蓝图。
• 通过训练数据和优化算法（反向传播等操作），我们**学习（确定）了这些未知参数 $w_i,b_i,c_i$ 的具体数值。
• 一旦这些参数的数值被学习确定下来，整个模型就变成了一个具体的、参数已知的函数。
• 我们使用这个参数已知的函数和学习到的参数值来对新的输入数据进行预测。

2.1.4 模型的未知参数集 ($\theta$) (The Set of Unknown Parameters in the Model, $\theta$)

在我们定义的神经网络模型中，例如单隐藏层网络：

存在一系列需要通过从数据中学习来确定的未知参数 (Unknown parameters)。

这些参数具体包括：

1. 输入层到隐藏层的权重矩阵 ($W$):

   • 这是一个矩阵，其维度通常是 (隐藏层神经元数量 $N_1$) $\times$ (输入特征数量 $N_0$)。
   • 它包含了连接每个输入特征到每个隐藏层神经元的所有权重。

2. 隐藏层的偏置向量 (${\mathbf{b}}_{hidden}$):

   • 这是一个列向量，其维度是 (隐藏层神经元数量 $N_1$) $\times 1$。
   • 图 8.png 中用绿色的 b 表示（为了区分，我们这里用 ${\mathbf{b}}_{hidden}$）。
   • 它包含了每个隐藏层神经元的偏置项。

3. 隐藏层到输出层的权重向量 (${\mathbf{c}}^T$ 或 $\mathbf{c}$):

   • 如果输出 $y$ 是一个标量（如回归或二分类的logit），那么 ${\mathbf{c}}^T$ 是一个行向量，维度是 $1\times$ (隐藏层神经元数量 $N_1$)。或者其转置 $\mathbf{c}$ 是一个列向量，维度是 ($N_1\times 1$)。
   • 图 8.png 中用橙色的 c^T 表示。
   • 它包含了连接每个隐藏层神经元到输出单元的权重。

4. 输出层的偏置 ($b_{output}$):

   • 这是一个标量值。
   • 图 8.png 中用灰色的 b 表示（为了区分，我们这里用 $b_{output}$）。
   • 它是输出单元的偏置项。

将所有参数集合为单一向量 $\theta$:

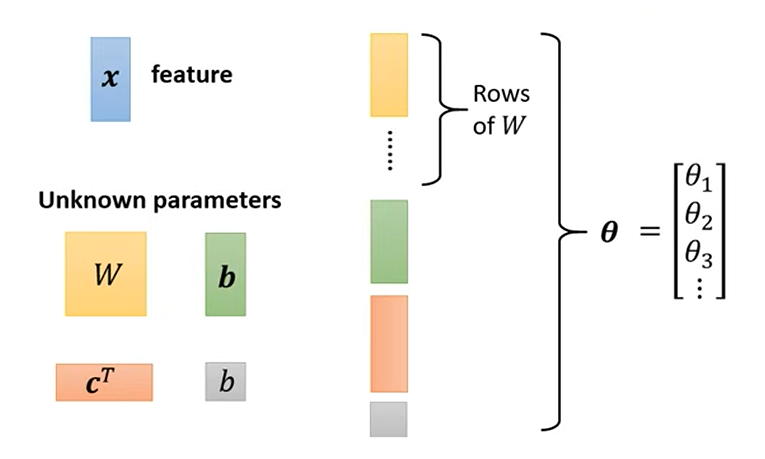
为了在后续的优化过程中（例如使用梯度下降）更方便地处理这些不同形状和类型的参数，通常会将它们全部 “展平 (flattened)” 并按特定顺序串联起来，形成一个单一的、非常长的参数向量 $\theta$**。

如图 8.png 所示，这个参数向量 $\theta$ 可以这样构成：

• 首先是权重矩阵 $W$ 的所有元素（例如，可以逐行或逐列展开）。
• 然后是隐藏层偏置向量 ${\mathbf{b}}_{hidden}$ 的所有元素。
• 接着是输出层权重向量 ${\mathbf{c}}^T$ (或 $\mathbf{c}$) 的所有元素。
• 最后是输出层偏置 $b_{output}$。

所以，这个参数向量 $\theta$ 可以表示为：

其中 $K$ 是模型中所有独立参数的总数量。例如，如果 $W$ 是 $N_1\times N_0$，$b_{hidden}$ 是 $N_1\times 1$，${\mathbf{c}}^T$ 是 $1\times N_1$，$b_{output}$ 是标量，则 $K=N_1\cdot N_0+N_1+N_1+1$。

模型函数以 $\theta$ 为参数:
通过这种方式，我们可以将整个神经网络模型函数 $f$ 视为以输入 $\mathbf{x}$ 和这个单一的参数向量 $\theta$ 为参数的函数：

下一步：
在明确了模型的函数形式 $f(\mathbf{x};\theta )$ 并识别出所有未知参数 $\theta$ 之后，机器学习的下一步骤将是定义一个代价函数来评估使用特定 $\theta$ 时模型的表现，然后使用优化算法来找到使代价函数最小化的最优 ${\theta }^{\ast }$。

2.1.5 模型的扩展：从回归到多分类 (Extending the Model: From Regression to Multi-class Classification)

到目前为止，我们讨论的模型（例如 $y=b+\sum _i{c}_i{a}_i$）主要用于回归任务，即预测一个连续的数值。但是，许多现实世界的问题是分类任务，特别是多分类 (Multi-class Classification)，例如将图像识别为“猫”、“狗”或“鸟”。

为了让我们的神经网络能够处理多分类问题，我们需要对模型的输出层进行修改。

1. 修改输出层结构:

   • 在回归任务中，输出层通常只有一个神经元，输出一个标量值。
   • 在一个有 $K$ 个类别的多分类任务中，输出层需要有 $K$ 个神经元，每个神经元对应一个类别。
   • 网络最后一层在激活函数之前的输出，我们称之为 logits。对于一个输入样本 $\mathbf{x}$，模型会输出一个包含 $K$ 个分数的向量 $\mathbf{z}=[z_1,z_2,\dots ,z_K]$。其中，$z_i$ 可以被看作是模型认为输入样本属于第 $i$ 类的原始置信度分数。

2. 转换输出为概率分布:

   • 这些原始的 logits 分数（$z_i$）可以是任意实数（正数、负数或零），并且它们的和不一定为 1。这不符合我们对“概率”的直观理解。
   • 我们需要一个函数，能将这个 logits 向量 $\mathbf{z}$ 转换成一个有效的概率分布向量 $\hat{\mathbf{y}}$，其中每个元素 ${\hat{y}}_i$ 表示样本属于第 $i$ 类的概率。这个概率分布需要满足两个条件：
     1. 所有概率值都在 0 和 1 之间 ($0\le {\hat{y}}_i\le 1$)。
     2. 所有概率值之和为 1 ($\sum _{i=1}^K{\hat{y}}_i=1$)。
   • 这个转换函数就是 Softmax 函数。

2.1.6 输出层激活函数：Softmax (Output Layer Activation: Softmax)

Softmax 函数通常用作多分类神经网络输出层的激活函数。它接收一个包含 $K$ 个实数值的向量（logits），并将其转换为一个 $K$ 维的概率分布。

定义与计算 (Definition and Calculation):

如上图所示，假设神经网络的输出层在应用 Softmax 之前的原始输出（logits）为向量 ${\mathbf{y}}_{raw}=[y_1,y_2,\dots ,y_K]$ (注意：此处的 $y_i$ 对应我们之前提到的 logits $z_i$)。Softmax 函数计算得到最终的概率输出 ${\mathbf{y}}^{\prime }=[y_1^{\prime },y_2^{\prime },\dots ,y_K^{\prime }]$ (此处的 $y_i^{\prime }$ 对应我们最终的预测概率 ${\hat{y}}_i$)。

对于第 $i$ 个类别的概率 $y_i^{\prime }$，其计算公式为：

计算步骤:

1. 取指数 (Exponentiate): 对每一个原始输出分数 $y_i$ 应用指数函数 $\exp (\cdot )$。这有两个作用：
   • 将所有值（包括负数和零）映射到正数。
   • 放大不同分数之间的差异，使得较大的分数在指数化后变得更大。
2. 求和 (Sum): 将所有指数化后的值 $\exp (y_j)$ 相加，得到一个归一化常数。
3. 归一化 (Normalize): 将每个指数化后的值 $\exp (y_i)$ 除以这个总和。

经过 Softmax 处理后，输出向量 ${\mathbf{y}}^{\prime }$ 的每个元素 $y_i^{\prime }$ 都在 [0, 1] 区间内，并且所有元素的总和为 1，因此可以被完美地解释为模型预测的概率分布。$y_i^{\prime }$ 就代表了模型预测输入样本属于类别 $i$ 的概率。

2.2 步骤二：定义代价函数/损失函数以评估模型 (Step 2: Define Cost/Loss Function to Evaluate the Model)

在步骤一 (2.1) 中，我们定义了一个带有未知参数 $\theta$ 的模型函数 $y=f(\mathbf{x};\theta )$。现在，我们需要一种方法来衡量这个模型在使用特定参数集 $\theta$ 时，其预测结果与真实目标值之间的差异有多大。这个衡量标准就是代价函数 (Cost Function) 或 损失函数 (Loss Function)。

2.2.1 代价函数/损失函数 (Cost Function / Loss Function)

• 定义 (Definition):

  • 损失函数 $L(\theta )$ 是一个关于模型参数 $\theta$ 的函数。
  • 它量化了模型在使用当前参数 $\theta$ 时，在整个训练数据集上预测的好坏程度 (Loss means how good a set of value is / how bad the current set of parameters is)。
  • 损失值越小，表示模型的预测越接近真实值，即当前这组参数 $\theta$ 的表现越好。

• 计算方法 (How it's Calculated):

  1. 单个样本的损失 (Loss for a single example):
     对于训练集中的每一个样本 $(x^{(n)},y_{true}^{(n)})$ (其中 $n$ 是样本索引)，我们首先计算模型在该样本上的预测值 ${\hat{y}}^{(n)}=f(x^{(n)};\theta )$。
     然后，我们使用一个损失度量 (loss metric) $e_n$ 来计算预测值 ${\hat{y}}^{(n)}$ 与真实值 $y_{true}^{(n)}$ 之间的差异。常见的损失度量有：

     • 均方误差 (Mean Squared Error, MSE): $e_n=({\hat{y}}^{(n)}-y_{true}^{(n)}{)}^2$
     • 交叉熵 (Cross-Entropy) (常用于分类): 具体形式取决于任务。

  2. 整个训练集的总损失/平均损失 (Total/Average Loss over the Training Set):
     代价函数 $L(\theta )$ 通常是所有训练样本损失的平均值（或总和）。如果训练集有 $N_{total}$ 个样本：

     $$L(\theta )=\frac{1}{N_{total}}\sum _{n=1}^{N_{total}}{e}_n=\frac{1}{N_{total}}\sum _{n=1}^{N_{total}}\text{loss-metric}(f(x^{(n)};\theta ),y_{true}^{(n)})$$

• 损失函数的具体例子: (这里可以链接到你之前整理的更详细的损失函数列表，或者简要重述)

  • 回归问题: 均方误差 (MSE)
  • 二分类问题: 二元交叉熵 (Binary Cross-Entropy)
  • 多分类问题: 分类交叉熵 (Categorical Cross-Entropy)

• 使用 Mini-batch 计算损失 (Calculating Loss using Mini-batches):
  在实际训练深度神经网络时，由于训练数据集通常非常大，一次性计算整个数据集上的损失 $L(\theta )$ 可能会非常耗时且占用大量内存。因此，我们通常采用 Mini-batch 梯度下降 深度学习 (Deep Learning)#2.1. Mini-batch 梯度下降 (Mini-batch Gradient Descent)。

  • Mini-batch Loss: 在每次迭代中，我们从训练数据中抽取一小批样本 (a mini-batch)，例如包含 $B$ 个样本。然后，我们计算模型在这 $B$ 个样本上的平均损失，并将其作为对整个训练集损失 $L(\theta )$ 的一个估计或代理 (proxy)。$$L_{batch}(\theta )=\frac{1}{B}\sum _{k=1}^B\text{loss-metric}(f(x_{batch}^{(k)};\theta ),y_{true,batch}^{(k)})$$优化算法将尝试最小化这个 $L_{batch}(\theta )$。
  • Epoch: 当算法处理完训练数据集中所有的 mini-batches，即对整个训练数据集完整地过了一遍之后，称为完成了一个 epoch (1 epoch = see all the batches once)。

• 损失函数的角色 (The Role of the Loss Function):
  损失函数不仅告诉我们当前这组参数 $\theta$ 的表现如何，更重要的是，它的梯度将指导我们如何调整这些参数以改进模型。

2.2.2 分类问题的损失函数：交叉熵 (Loss Function for Classification: Cross-Entropy)

现在我们有了模型的概率输出 $\hat{\mathbf{y}}$（即 Softmax 的输出 ${\mathbf{y}}^{\prime }$），我们需要一个损失函数来衡量这个预测的概率分布与真实的类别标签之间的差距。对于分类问题，最常用的损失函数是交叉熵损失 (Cross-Entropy Loss)。

真实标签的表示：One-Hot 编码

首先，我们需要将真实的类别标签表示成和模型输出相同维度的概率分布。这通常通过 One-Hot 编码实现。如果一个样本的真实类别是第 $k$ 类（在一个共 $K$ 个类别的任务中），那么它的 One-Hot 编码向量 ${\mathbf{y}}_{true}$ 就是一个长度为 $K$ 的向量，其中第 $k$ 个元素为 1，其余所有元素都为 0。

• 例子: 对于三分类问题（猫、狗、鸟），如果一个样本是“狗”（第2类），它的 One-Hot 标签就是 $[0,1,0]$。

交叉熵损失的计算

交叉熵损失衡量了两个概率分布之间的“距离”。给定真实标签的 One-Hot 向量 ${\mathbf{y}}_{true}$ 和模型预测的概率向量 $\hat{\mathbf{y}}$，交叉熵损失 $L$ 的计算公式为：

• 由于 ${\mathbf{y}}_{true}$ 是 One-Hot 编码，其中只有一个元素为 1（假设是第 $c$ 个元素，代表正确类别），其余都为 0。因此，上述求和可以简化为：

  $$L(\theta )=-\log ({\hat{y}}_c)$$

  其中 ${\hat{y}}_c$ 是模型预测输入样本为正确类别的概率。

• 直观理解:

  • 最小化交叉熵损失 $L=-\log ({\hat{y}}_c)$，等价于最大化正确类别的预测概率 ${\hat{y}}_c$。
  • 当模型对正确类别的预测概率 ${\hat{y}}_c$ 接近 1 时，$\log ({\hat{y}}_c)$ 接近 0，损失 $L$ 也接近 0。
  • 当模型对正确类别的预测概率 ${\hat{y}}_c$ 接近 0 时，$\log ({\hat{y}}_c)$ 趋向于 $-\mathrm{\infty }$，损失 $L$ 趋向于 $+\mathrm{\infty }$。

这样，通过使用 Softmax 输出层和交叉熵损失函数，我们可以构建和训练用于解决多分类问题的深度神经网络，并通过梯度下降等优化算法来调整参数 $\theta$，使得模型对正确类别的预测概率越来越高。

2.3 步骤三：参数优化 (Step 3: Optimization)

一旦我们定义了模型 $f(\mathbf{x};\theta )$ 和损失函数 $L(\theta )$，我们的目标就是找到一组最优的参数 ${\theta }^{\ast }$，使得损失函数 $L(\theta )$ 的值最小。这个寻找最优参数的过程称为优化 (Optimization)。

数学上，我们可以表示为：

这意味着我们要寻找使损失函数 $L$ 达到最小值的参数向量 $\theta$。

2.3.1 核心优化算法：梯度下降及其变体

2.3.1.1 梯度下降 (Gradient Descent)

梯度下降是一种广泛应用于机器学习和深度学习中的迭代优化算法，用于寻找函数的最小值。其基本思想是沿着损失函数梯度下降最快的方向逐步调整参数。

梯度下降的步骤:

1. 初始化参数 (Initialize Parameters):

   • 随机选择或根据某种策略设定参数向量 $\theta$ 的初始值，记为 ${\theta }^0$。(Randomly) Pick initial values ${\theta }^0$.

2. 迭代更新 (Iteratively Update): 重复以下操作直到满足停止条件：

   • a. 计算梯度 (Compute Gradient):

     • 计算损失函数 $L(\theta )$ 在当前参数点 ${\theta }^t$ (其中 $t$ 是迭代次数) 关于参数向量 $\theta$ 中每一个分量 ${\theta }_k$ 的偏导数。这些偏导数共同构成了损失函数在 ${\theta }^t$ 处的梯度向量 (gradient vector) $\mathbf{g}$ (或 $\mathrm{\nabla }L({\theta }^t)$)。$$\mathbf{g}=\mathrm{\nabla }L({\theta }^t)={\left(\begin{array}{c}\frac{\partial L}{\partial {\theta }_1}\\ \frac{\partial L}{\partial {\theta }_2}\\ ⋮\\ \frac{\partial L}{\partial {\theta }_K}\end{array}\right)}_{\theta ={\theta }^t}$$
     • 在神经网络中，这个梯度通常通过反向传播 (Backpropagation) 算法高效计算。
     • 当使用 mini-batch 时，计算的是 $L_{batch}(\theta )$ 的梯度。
       
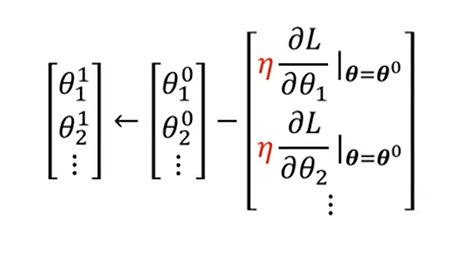
     • (图示：梯度指向函数增加最快的方向)

   • b. 更新参数 (Update Parameters):

     • 根据梯度信息，沿着梯度的反方向更新参数，以减小损失函数的值。$${\theta }^{t+1}\leftarrow {\theta }^t-\eta \cdot \mathbf{g}$$或者写成：$${\theta }^{t+1}\leftarrow {\theta }^t-\eta \mathrm{\nabla }L({\theta }^t)$$
     • 其中：
       • ${\theta }^{t+1}$ 是更新后的参数向量。
       • ${\theta }^t$ 是当前迭代的参数向量。
       • $\eta$ (eta) 是学习率 (Learning Rate)，它是一个正的小值（超参数），控制每次参数更新的“步长”或幅度。学习率的选择对训练过程至关重要。
       • $\mathbf{g}$ (或 $\mathrm{\nabla }L({\theta }^t)$) 是在 ${\theta }^t$ 处计算得到的梯度向量。

3. 停止条件 (Stopping Condition):

   • 可以设定最大迭代次数 (或最大 epoch 数)。
   • 可以监控损失函数的值，当其变化很小或不再下降时停止。
   • 可以监控在验证集上的性能，当验证集性能不再提升（甚至开始下降，表明过拟合）时停止（早停法 Early Stopping）。

2.3.1.2 批量大小的选择 (The Choice of Batch Size)

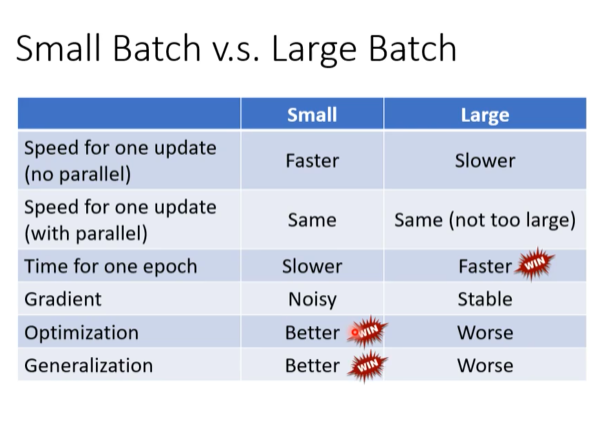
在实践中，我们很少一次性使用整个训练集来计算梯度并更新参数。相反，我们会根据每次更新所使用的样本数量，将梯度下降分为三种主要类型。批量大小 (Batch Size) 的选择是一个重要的超参数，它在计算效率和模型性能之间做出了权衡。

• 批量梯度下降 (Batch Gradient Descent / Full Batch): 批量大小 = N (整个数据集)。
• 随机梯度下降 (Stochastic Gradient Descent, SGD): 批量大小 = 1。
• 小批量梯度下降 (Mini-batch Gradient Descent): 批量大小介于 1 和 N 之间，是现代深度学习的标准做法。

但是由于GPU的并行运算，在数据集较小的时候，Mini-batch GD不一定比Batch GD快

2.3.1.3 动量法 (Momentum)

为了解决梯度下降在狭窄山谷中震荡和在平坦区域停滞的问题，可以引入动量 (Momentum)。

• 核心思想: 模拟物理惯性。参数的更新方向不仅取决于当前梯度，还受历史累积的更新方向影响。
  

  • 一个从山上滚下的小球，其惯性（动量）能帮助它冲过小的坑洼（局部最小值）和平台（鞍点），并平滑掉在山谷两侧的震荡。

• 算法:

  1. 计算当前梯度: ${\mathbf{g}}^t=\mathrm{\nabla }L({\theta }^{t-1})$
  2. 更新动量向量: ${\mathbf{m}}^t=\lambda {\mathbf{m}}^{t-1}+{\mathbf{g}}^t$ (其中 $\lambda$ 是动量衰减因子，通常为0.9)
  3. 更新参数: ${\theta }^t={\theta }^{t-1}-\eta {\mathbf{m}}^t$
  4. 初始值: $m_0=0,m^1=-\eta g^0,m^2=-\lambda \eta g^0-\eta g^1,\cdots$

• 效果:

  • 加速收敛: 在梯度方向一致的区域，动量累积，步长增大。
  • 减少震荡: 在梯度方向反复震荡的区域，动量会抵消掉相反方向的更新。

2.3.2 优化中的泛化与几何视角

2.3.2.1 批量大小对模型泛化能力的影响

除了影响训练速度和稳定性，批量大小还会对模型的泛化能力 (Generalization Performance) 产生显著影响。泛化能力指的是模型在未见过的测试数据上的表现，通常用验证集准确率 (validation accuracy) 来衡量。

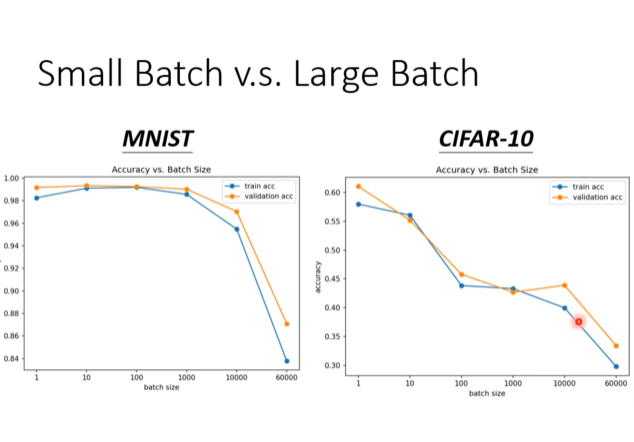
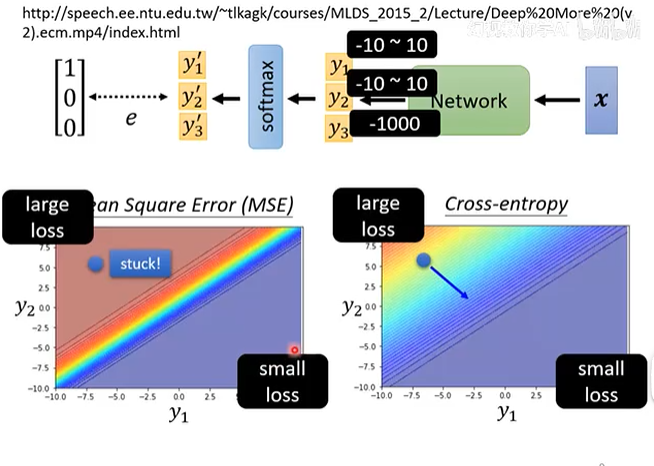
上图展示了在两个不同的数据集（MNIST 和 CIFAR-10）上，最终达到的训练准确率（train acc）和验证准确率（validation acc）与批量大小（batch size）的关系。

关键观察 (Key Observations):

1. 大批量 (Large Batch) 倾向于损害泛化能力:

   • 在这两个实验中，当批量大小变得非常大时（例如，超过1000），验证集准确率（橙色线） 明显下降。
   • 这意味着虽然模型在训练集上可能表现尚可（虽然训练准确率也在下降），但它在新数据上的表现变差了。我们称之为泛化差距 (Generalization Gap) 变大。

2. 小批量 (Small Batch) 通常能获得更好的泛化能力:

   • 使用较小的批量大小（例如，1到几百之间）时，模型在验证集上取得了更高的准确率。
   • 这表明小批量训练出的模型具有更好的泛化能力。

为什么会出现这种现象？—— 损失曲面的“平坦度”

一个被广泛接受的解释是，小批量梯度下降所引入的噪声有助于优化过程找到更“平坦”的局部最小值，而大批量梯度下降倾向于收敛到更“尖锐”的局部最小值。

• 平坦的最小值 (Flat Minima): 像一个宽阔的盆地。即使测试数据与训练数据的分布有轻微差异，模型参数在这个盆地里稍微移动一下，损失值的变化也不大。因此，模型对新数据的适应性更强，泛化能力更好。小批量梯度下降的噪声使其难以在尖锐的谷底稳定下来，更容易在宽阔的盆地中找到平衡。

• 尖锐的最小值 (Sharp Minima): 像一个狭窄的深谷。模型在训练集上可能达到了极低的损失，但只要测试数据的分布稍有不同，参数的微小偏离就会导致损失值急剧上升。因此，模型泛化能力差。大批量梯度下降的平滑路径使其能够精确地滑入这种尖锐的谷底。

论文实证：《On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima》

这篇著名的论文 (https://arxiv.org/abs/1609.04836) 通过大量实验系统地验证了这一现象。

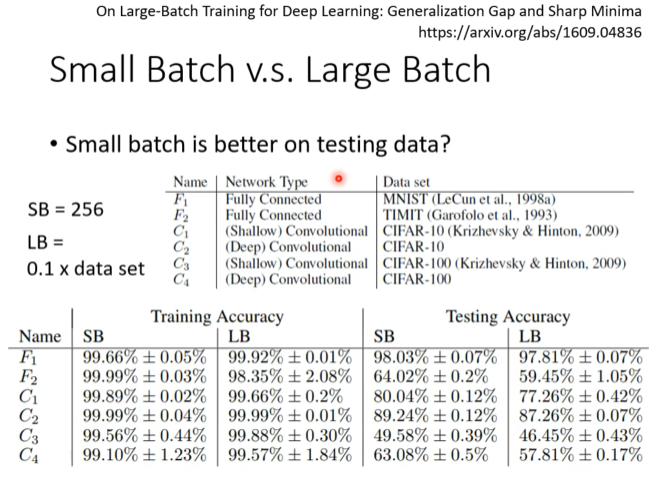
• 实验设置:

  • 小批量 (Small Batch, SB): 固定为 256。
  • 大批量 (Large Batch, LB): 设置为数据集大小的 10%。
  • 在多种网络架构（全连接、浅层/深层卷积网络）和多个数据集（MNIST, TIMIT, CIFAR-10, CIFAR-100）上进行对比。

• 实验结论:

  • 在测试数据上，小批量总是更好 (Small batch is better on testing data?): 表格中的 "Testing Accuracy" 一栏清楚地显示，对于所有实验（F1, F2, C1-C4），SB 的测试准确率都显著高于 LB 的测试准确率。
  • 训练准确率不代表一切: 尽管在某些情况下，大批量（LB）的训练准确率（Training Accuracy）可以与小批量（SB）相媲美，甚至更高，但这并没有转化为更好的泛化能力。

为什么“带噪声”的更新更好？

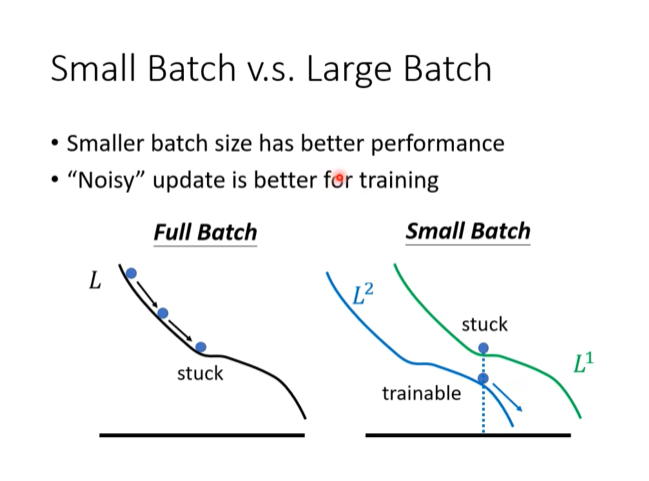
这张示意图从另一个角度解释了为什么小批量的噪声更新是有益的。

• Full Batch (左图):

  • 使用全批量计算的梯度指向的是整个训练集的平均损失 $L$ 的下降方向。
  • 优化过程沿着平滑的路径下降，如果它进入一个“尖锐”的局部最小值（图中所示），它就会被困住 (stuck)，因为在该点的梯度为零。

• Small Batch (右图):

  • 在同一点，不同的小批量数据会产生不同的损失函数曲面（例如 $L^1$ 和 $L^2$）。
  • 在一次更新中，模型可能看到的是 $L^1$ 的损失曲面，并沿着其梯度方向移动。
  • 在下一次更新中，它看到的是 $L^2$ 的损失曲面，并沿着新的梯度方向移动。
  • 即使模型在某一个批次的损失曲面（如 $L^1$）上看起来被困住 (stuck) 了，但下一个批次（如 $L^2$）会提供一个不同的、通常非零的梯度，使得模型能够继续训练 (trainable) 和移动。
  • 这种由不同 mini-batch 带来的“抖动”和“噪声”，使得优化过程能够探索更广泛的参数空间，避免过早地陷入第一个遇到的（可能很差的）局部最小值。

总结：

• 小批量：训练速度快（按更新次数算），噪声大，有助于模型跳出坏的局部极值，并找到泛化能力更好的“平坦”最小值。实验数据和理论分析都表明，较小的批量通常能带来更好的测试性能。
• 大批量：梯度计算稳定，但计算成本高，且容易收敛到泛化能力较差的“尖锐”最小值。

因此，在实践中，选择一个合适的（不大也不太小）的 mini-batch size（如32, 64, 128, 256等）是在训练效率和模型最终性能之间取得平衡的关键策略。

2.3.2.2 优化进阶：泰勒展开与损失曲面近似 (Advanced Optimization: Taylor Expansion & Loss Surface Approximation)

在梯度下降中，我们利用损失函数的一阶导数（梯度）来确定下降方向。为了更深入地理解优化过程，特别是更高级的优化算法（如牛顿法），我们可以使用泰勒级数 (Taylor Series) 来近似损失函数。

泰勒展开的核心思想是，在任意一个参数点 ${\theta }^{\prime }$ 附近，我们可以用一个更简单的多项式函数来近似复杂的损失函数 $L(\theta )$。对于优化而言，通常使用到二阶的泰勒展开就足够了。

如上图所示，在点 ${\theta }^{\prime }$ 附近的二阶泰勒展开为：

• $L({\theta }^{\prime })$: 当前点 ${\theta }^{\prime }$ 的损失值，这是一个常数。
• $(\theta -{\theta }^{\prime }{)}^{T}g$: 一阶项 (First-order term)。
  • $\mathbf{g}=\mathrm{\nabla }L({\theta }^{\prime })$ 是损失函数在点 ${\theta }^{\prime }$ 的梯度 (Gradient)。
  • 这一项用一个线性函数来近似损失函数的变化。梯度下降法只依赖于这一项，它告诉我们在 ${\theta }^{\prime }$ 附近，沿着负梯度 $-\mathbf{g}$ 的方向移动，损失值 $L(\theta )$ 会下降得最快。图中的绿色框和绿色直角三角形的高度就直观地表示了这一线性近似。
• $\frac{1}{2}(\theta -{\theta }^{\prime }{)}^{T}H(\theta -{\theta }^{\prime })$: 二阶项 (Second-order term)。
  • $H$ 是损失函数在点 ${\theta }^{\prime }$ 的海森矩阵 (Hessian Matrix)，即损失函数的二阶偏导数矩阵 ($H_{ij}=\frac{{\partial }^{2}L}{\partial {\theta }_i\partial {\theta }_j}$)。
  • 这一项引入了关于损失曲面曲率 (curvature) 的信息。它用一个二次函数来更精确地描述损失曲面的形状（是“平坦”的碗还是“陡峭”的碗）。

临界点分析 (Analysis at Critical Points)

当梯度下降进行到某一步时，如果梯度 $\mathbf{g}=\mathrm{\nabla }L({\theta }^{\prime })=0$，我们称 ${\theta }^{\prime }$ 为一个临界点 (Critical Point)。在临界点，梯度下降会停止更新，因为它找不到下降的方向。此时，泰勒展开的一阶项为零，损失函数的行为完全由二阶项决定：

令 $\mathbf{v}=(\theta -{\theta }^{\prime })$，我们可以通过海森矩阵 $H$ 的性质来判断这个临界点的类型：

• 如果对于所有非零向量 $\mathbf{v}$，都有 ${\mathbf{v}}^{T}H\mathbf{v}>0$（即 $H$ 是正定矩阵），那么 $L(\theta )>L({\theta }^{\prime })$。这意味着 ${\theta }^{\prime }$ 是一个局部最小值点 (Local Minima)。
• 如果对于所有非零向量 $\mathbf{v}$，都有 ${\mathbf{v}}^{T}H\mathbf{v}<0$（即 $H$ 是负定矩阵），那么 $L(\theta )<L({\theta }^{\prime })$。这意味着 ${\theta }^{\prime }$ 是一个局部最大值点 (Local Maxima)。
• 如果对于某些向量 $\mathbf{v}$，${\mathbf{v}}^{T}H\mathbf{v}>0$，而对于另一些向量 $\mathbf{v}$，${\mathbf{v}}^{T}H\mathbf{v}<0$（即 $H$ 是不定矩阵），那么 ${\theta }^{\prime }$ 是一个鞍点 (Saddle Point)。

如何逃离鞍点 (Don't be afraid of Saddle Point!)

在高维空间中（例如深度神经网络的参数空间），鞍点远比局部最小值点更常见。那么，当梯度下降卡在鞍点时（因为梯度为零），我们该怎么办呢？海森矩阵 $H$ 告诉了我们逃离的方向！
鞍点的最速逃离方向 (The fastest escape direction for the stationed point)

• 核心思想: 在鞍点处，海森矩阵 $H$ 必然存在至少一个负特征值 (negative eigenvalue)。

• 逃离步骤:

  1. 假设我们当前在鞍点 ${\theta }^{\prime }$，梯度为零。
  2. 我们计算海森矩阵 $H$ 的特征值和特征向量。
  3. 找到一个负特征值 $\lambda <0$ 以及其对应的特征向量 $\mathbf{u}$。
  4. 根据特征向量的定义，我们有 $H\mathbf{u}=\lambda \mathbf{u}$。
  5. 现在，我们考虑沿着特征向量 $\mathbf{u}$ 的方向更新参数，即令更新步长 $\theta -{\theta }^{\prime }=\mathbf{u}$。
  6. 代入泰勒展开式，计算新的损失值与当前损失值的差异：$$L(\theta )-L({\theta }^{\prime })\approx \frac{1}{2}(\theta -{\theta }^{\prime }{)}^{T}H(\theta -{\theta }^{\prime })=\frac{1}{2}{\mathbf{u}}^{T}H\mathbf{u}$$利用 $H\mathbf{u}=\lambda \mathbf{u}$，我们得到：$$\frac{1}{2}{\mathbf{u}}^T(H\mathbf{u})=\frac{1}{2}{\mathbf{u}}^T(\lambda \mathbf{u})=\frac{1}{2}\lambda ({\mathbf{u}}^T\mathbf{u})=\frac{1}{2}\lambda ||\mathbf{u}|{|}^2$$
  7. 因为 $\lambda <0$ 且 $||\mathbf{u}|{|}^2>0$，所以 $\frac{1}{2}\lambda ||\mathbf{u}|{|}^2<0$。
  8. 这意味着 $L(\theta )-L({\theta }^{\prime })<0$，即 $L(\theta )<L({\theta }^{\prime })$。

• 结论: 只要我们沿着海森矩阵负特征值对应的特征向量方向更新参数（例如，$\theta ={\theta }^{\prime }+\alpha \mathbf{u}$，其中 $\alpha$ 是一个小的步长），我们就能有效地降低损失值，从而成功逃离鞍点。

实际应用中的意义:

虽然在大型神经网络中显式地计算整个海森矩阵及其特征向量的成本极高，但这个理论非常重要：

1. 它解释了为什么鞍点在理论上不是一个根本性的障碍。总有“下山”的路可走。
2. 许多先进的优化算法，如带动量的SGD、Adam等，虽然没有直接计算海森矩阵，但它们引入的机制（如动量）在实践中能帮助模型“冲过”平坦区域和鞍点。
3. 一些二阶优化算法的变体（如Hessian-Free优化）会尝试用更高效的方法来近似海森矩阵与某个向量的乘积（即 $H\mathbf{v}$），从而利用曲率信息来逃离鞍点和加速收敛。

与优化的关系:

1. 梯度下降 (Gradient Descent): 只考虑一阶信息（梯度 g），可以看作是在一个线性的近似下寻找下降方向。它简单高效，但不知道“走多远”最合适（需要手动设置学习率 $\eta$），也无法很好地处理不同方向上曲率差异很大的情况（例如狭长的山谷）。

2. 牛顿法 (Newton's Method): 同时考虑一阶（梯度 g）和二阶信息（海森矩阵 H）。它通过找到上述二次近似函数的最小值点来确定下一步的更新方向和步长。更新规则为 ${\theta }^{t+1}={\theta }^t-H^{-1}g$。

   • 优点: 收敛速度通常比梯度下降快得多，因为它利用了曲率信息，能够更直接地跳向最小值点。
   • 缺点: 计算和存储海森矩阵 $H$ 以及其逆矩阵 $H^{-1}$ 的开销巨大。对于有数百万参数的深度神经网络来说，这是不现实的。

因此，在深度学习中，虽然我们不直接使用标准的牛ton法，但许多先进的优化器（如 Adam、RMSProp 等）都受到了“利用曲率信息来调整步长”这一思想的启发，它们通过各种方式来近似海森矩阵的信息，以实现比朴素梯度下降更快的收敛。泰勒展开为理解这些高级优化算法提供了坚实的理论基础。

“最小比率”：一个用于分析损失曲面几何的指标 (The "Minimum Ratio": A Metric for Analyzing Loss Surface Geometry)

重要澄清: 此处讨论的 "Minimum ratio" 是一个用于分析海森矩阵特性的指标，与线性规划单纯形法 (Simplex Method) 中的 "Minimum Ratio Test" 完全无关。

在深度学习的优化研究中，研究者们有时会使用一个比率来量化损失函数在某个特定点 $\theta$ 附近的几何形状，特别是判断它有多像一个真正的“谷底”（局部最小值）。你提供的图片中就定义了这样一个比率：

这个指标的意义是什么？

这个比率衡量了在当前点，损失曲面在所有主轴方向中，有多少个方向是“向上弯曲”的（即具有正曲率）。

• 分母 (Total Number of Eigenvalues): 等于模型参数的总数量。它代表了参数空间的总维度。
• 分子 (Number of Positive Eigenvalues): 代表了海森矩阵 H 的正特征值的数量。我们知道，每个正特征值对应一个向上弯曲的（类似山谷的）方向。

如何解读这个比率的值？

1. 当 Ratio ≈ 1.0 时:

   • 这意味着几乎所有的特征值都是正的。
   • 海森矩阵 H 近似于一个正定矩阵。
   • 当前点 $\theta$ 的几何形状非常像一个真正的局部最小值，即一个在所有方向上都向上弯曲的“碗”或“盆地”。在优化过程中，我们希望找到的就是这样的点。

2. 当 Ratio ≈ 0.5 时:

   • 这意味着大约一半的特征值是正的，另一半是负的。
   • 这是鞍点 (Saddle Point) 的一个典型特征。损失曲面在很多方向上向上弯，但在同样多的方向上向下弯。

3. 当 Ratio ≈ 0.0 时:

   • 这意味着几乎所有的特征值都是负的。
   • 海森矩阵 H 近似于一个负定矩阵。
   • 当前点 $\theta$ 的几何形状非常像一个局部最大值，即一个在所有方向上都向下弯曲的“山峰”。

为什么叫 "Minimum ratio"？

这个名字可能有些令人困惑。一个可能的解释是，这个比率是用来分析和表征损失函数的最小值点 (loss minimum) 的。一个“好的”最小值点，其“Minimum ratio”应该接近1。因此，这个比率可以看作是衡量一个临界点“有多好”或者“有多像一个真正的最小值”的指标。在文献中，你可能也会看到它被称为正特征值比率 (Positive Eigenvalue Ratio) 或局部凸性比率 (Local Convexity Ratio)，这些名字可能更具描述性。

在训练过程中，模型参数从一个随机初始点开始，可能会经过许多“Minimum ratio”较低的区域（鞍点），最终收敛到一个“Minimum ratio”接近1的区域（一个好的局部最小值）。

注：

• 一个**神经元 (Neuron)**是一个基本的计算单元。
• 一个激活函数（如 Sigmoid）是神经元计算过程中的一个关键组成部分，它引入非线性。
• 当我们说“一个 Sigmoid 神经元”或在图中画一个 Sigmoid 符号时，我们通常指的就是一个以 Sigmoid 作为其激活函数的神经元/单元。
• 这整个体系，即由相互连接的“神经元”（或单元，每个单元执行加权求和与非线性激活函数如 Sigmoid、ReLU 等操作）组成的、分层的结构，就叫做神经网络 (Neural Network)。
• 如果这个网络包含多个隐藏层，它就是一个深度神经网络 (Deep Neural Network, DNN)
  对应关系是：
• 一个 Sigmoid (或其他激活函数) 是一个神经元计算的一部分。
• 多个神经元可以组成一个隐藏层 (Hidden Layer)。
• 多个隐藏层构成了一个深度神经网络

拓展：
1. 为什么我们要的是 "Deep" 的 network 而不是 "Fat" 的？
Deep 而非 Fat 的 Neural Network
2. 为什么我们不 "Deeper" ?
不一直 Deeper 的神经网络

2.3.2.3 优化再进阶：自适应学习率 (Adaptive Learning Rate)

在标准的梯度下降法中，所有参数共享同一个固定的学习率 $\eta$。然而，这往往不是最优的策略。

核心思想：不同的参数需要不同的学习率。

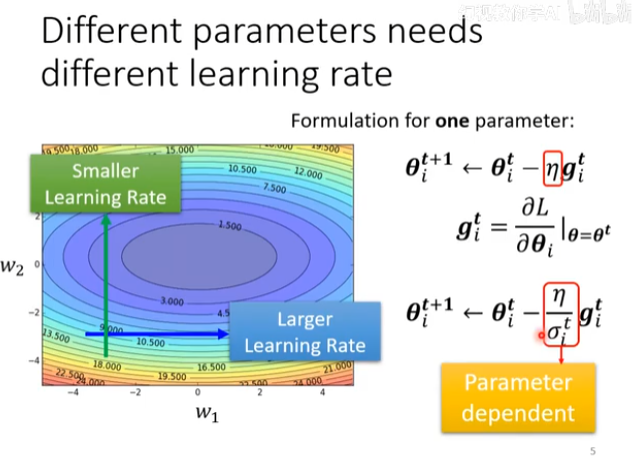
观察上图的损失曲面等高线图。这是一个狭长的“山谷”形状，是优化中非常典型的情况。

• 横轴 ($w_1$) 方向:

  • 这个方向非常平缓，梯度值很小。
  • 如果我们使用一个很小的学习率，那么在 $w_1$ 方向上的更新会非常缓慢，就像图中蓝色箭头所示，需要很多步才能前进一点点。
  • 因此，在平缓的方向上，我们需要一个较大的学习率 (Larger Learning Rate) 来加速收敛。

• 纵轴 ($w_2$) 方向:

  • 这个方向非常陡峭，梯度值很大。
  • 如果我们使用一个较大的学习率，那么在 $w_2$ 方向上的更新步长会非常大，导致参数在“山谷”的两壁之间剧烈震荡，甚至可能无法收敛，就像图中绿色箭头所示。
  • 因此，在陡峭的方向上，我们需要一个较小的学习率 (Smaller Learning Rate) 来保证稳定性和收敛。

这个矛盾揭示了固定学习率的局限性。一个理想的优化器应该能够自动地为每个参数调整学习率，即实现自适应学习率。

自适应学习率的数学形式

1. 标准梯度下降更新规则:

   • 对于第 i 个参数 ${\theta }_i$，其在第 t 次迭代的更新规则是：$${\theta }_i^{t+1}\leftarrow {\theta }_i^t-\eta g_i^t$$
   • 其中，$g_i^t=\frac{\partial L}{\partial {\theta }_i}{|}_{\theta ={\theta }^t}$ 是当前时刻的梯度。
   • 这里的学习率 η 是一个全局的、固定的超参数 (hyperparameter)。

2. 引入参数依赖的学习率:

   • 为了让学习率对每个参数“自适应”，我们可以将全局学习率 η 除以一个与该参数相关的项 ${\sigma }_i^t$。$${\theta }_i^{t+1}\leftarrow {\theta }_i^t-\frac{\eta }{{\sigma }_i^t}{g}_i^t$$
   • 这里的 $\frac{\eta }{{\sigma }_i^t}$ 就是第 i 个参数在第 t 时刻的有效学习率 (effective learning rate)。
   • 关键问题: 如何设计这个参数依赖 (Parameter dependent) 的项 ${\sigma }_i^t$？

如何设计 ${\sigma }_i^t$？

我们的目标是让陡峭方向的有效学习率变小，平缓方向的有效学习率变大。

• 陡峭方向的特点是：历史梯度值很大。
• 平缓方向的特点是：历史梯度值很小。

一个自然的想法就是，让 ${\sigma }_i^t$ 累积该参数过去所有梯度的大小。

• 如果参数 ${\theta }_i$ 的历史梯度一直很大（陡峭），那么 ${\sigma }_i^t$ 就会很大，导致有效学习率 $\frac{\eta }{{\sigma }_i^t}$ 变小。
• 如果参数 ${\theta }_i$ 的历史梯度一直很小（平缓），那么 ${\sigma }_i^t$ 就会很小，导致有效学习率 $\frac{\eta }{{\sigma }_i^t}$ 变大。

这正是许多先进优化算法的核心思想：

• Adagrad (Adaptive Gradient Algorithm):

  • 它将 ${\sigma }_i^t$ 定义为该参数历史梯度值的平方和的平方根。$${\sigma }_i^t=\sqrt{\sum _{k=0}^t(g_i^k{)}^2}$$
  • Adagrad 的更新规则就是：$${\theta }_i^{t+1}\leftarrow {\theta }_i^t-\frac{\eta }{\sqrt{\sum _{k=0}^t(g_i^k{)}^2}}{g}_i^t$$

• RMSProp (Root Mean Square Propagation) 和 Adam (Adaptive Moment Estimation):

  • 它们是对 Adagrad 的改进。Adagrad 有一个缺点：由于梯度平方和是单调递增的，学习率会随着训练不断下降，最终可能变得过小而导致训练提前停止。
  • RMSProp 和 Adam 引入了指数移动平均 (exponential moving average) 来计算 ${\sigma }_i^t$，只考虑最近一段时间的梯度大小，而不是全部历史梯度。这使得 ${\sigma }_i^t$ 能够动态调整，避免了学习率过早衰减的问题。
    
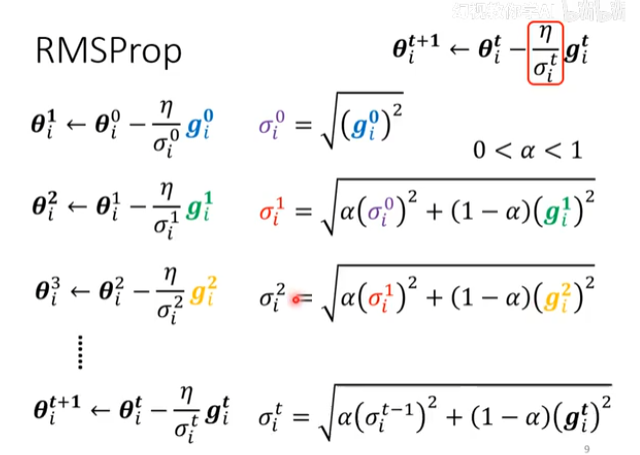
    总结:
    通过为每个参数设计一个依赖于其历史梯度大小的归一化项 ${\sigma }_i^t$，自适应优化算法能够有效地为不同参数分配不同的学习率，从而在面对复杂损失曲面（如狭长山谷）时，实现比标准梯度下降更快、更稳定的收敛。这为我们后续理解 Adagrad、RMSProp 和 Adam 等优化器奠定了基础。