Textbook: Syllabus | Information and Entropy | Electrical Engineering and Computer Science | MIT OpenCourseWare

Video: MIT6.050J information and entropy 001_哔哩哔哩_bilibili

Information is a change of entropy

Chapter 1: Bits

1.1 The Boolean Bit (布尔比特)

1.2 The Circuit Bit (电路比特)

Combinational logic circuits graphically represent Boolean expressions. Each Boolean function (NOT, AND, XOR, etc.) corresponds to a "combinational gate" with inputs and an output. Gates are connected by lines, forming circuits. A key property is that combinational circuits have no feedback loops; an output never feeds back into an input earlier in its own causal chain. Circuits with loops are called sequential logic, which Boolean algebra alone cannot describe. For instance, a NOT gate with its output connected directly to its input creates a contradiction under Boolean analysis.

• Core: Combinational logic circuits are gate-based, loop-free representations of Boolean operations.
• Distinction: Unlike sequential logic circuits (which have loops), they are fully describable by Boolean algebra.

组合逻辑电路是布尔表达式的图形化表示，其中每个布尔函数（如NOT, AND, XOR）对应一个有输入和输出的“组合逻辑门”。这些门通过连线将一个门的输出连接到其他门的输入，形成电路。关键特性是组合电路中没有反馈回路（即输出不会反过来影响产生该输出的链条上的任何输入）。存在回路的电路称为时序逻辑电路，布尔代数不足以描述它们。例如，一个NOT门的输出直接连回其输入，用布尔代数分析会产生矛盾。

• 核心: 组合逻辑电路由门构成，无环路，用于表示布尔运算。
• 区分: 与有环路的时序逻辑电路不同，后者不能简单用布尔代数描述。

1.3 The Control Bit (控制比特)

In programming, Boolean expressions often control execution flow (i.e., which statements run). The algebra of control bits differs interestingly from pure Boolean algebra: parts of a control expression not affecting the final result can be ignored (short-circuit evaluation). For example, in (if (and (< x 0) (> y 0)) ...), if x is found to be non-negative, the and operation is false regardless of y, so y isn't evaluated. This speeds up programs and avoids potential side effects from evaluating y.

• Core: Boolean logic used for program flow control.
• Key Difference: Features "short-circuit evaluation" for efficiency and side-effect avoidance.

在计算机程序中，布尔表达式常用于控制执行流程（即决定哪些语句被执行）。控制位代数与布尔代数的一个有趣区别是：表达式中不影响最终结果的部分可能被忽略（短路求值）。例如，在 (if (and (< x 0) (> y 0)) ...) 中，如果 x 不小于0，and 表达式的结果就确定为假，此时 y 的值无需判断，程序运行更快，且避免了评估 y 可能带来的副作用。

• 核心: 程序中用于控制流程的布尔逻辑。
• 关键区别: 存在“短路求值”特性，可提高效率并避免副作用。

1.4 The Physical Bit (物理比特)

Storing or transporting a bit requires a physical medium. This medium must have two distinguishable states, representing 0 and 1. A bit is stored by setting the medium to one state and read by measuring its state. Communication occurs if the bit's state is transferred between locations unchanged; memory if it persists over time. Engineering aims for smaller, faster, etc., physical bits. Quantum mechanics defines the ultimate smallness limit for bit storage, leading to the concept of the quantum bit (qubit).

• Core: Bits require a physical implementation with two distinct states.
• Development & Limit: Engineering drives improvements; quantum mechanics sets fundamental limits on size.

比特的存储或传输需要物理载体，该载体具有两种可区分的状态，分别代表0和1。通过将物体置于特定状态来存储比特，通过测量其状态来读取比特。信息通信即比特状态在不同位置间的无损转移，而内存则是比特状态随时间的持续保持。工程上追求更小、更快等的物理比特。量子力学设定了物体能存储信息的最小尺寸极限，引出了量子比特（qubit）。

• 核心: 比特需要物理实现，依赖于物体的两种可区分状态。
• 发展与极限: 工程驱动物理比特的改进，量子力学揭示了其小型化的根本限制。

1.5 The Quantum Bit (Qubit) (量子比特)

A qubit is a quantum mechanical system capable of storing a single bit, typically represented by two basis states, $|0⟩$ and $|1⟩$. Three key quantum mechanical features distinguish qubits (or collections of them) from classical Boolean bits: reversibility, superposition, and entanglement.

• Core: A bit based on quantum mechanical principles, denoted $|0⟩$ and $|1⟩$.
• Features: Reversibility, superposition, and entanglement differentiate it from classical bits.

Reversibility:
Quantum evolution is inherently reversible; if a state can transition to another, the reverse is also possible. Thus, quantum functions are reversible, and outputs cannot be discarded. However, irreversibility arises from a quantum system's interaction with an unknown environment (losing information) and from the act of measurement itself.

• Core: Quantum operations are fundamentally reversible.
• Exceptions: Interaction with the environment and measurement introduce irreversibility.

Superposition:
A qubit can exist in a superposition, a combination of its $|0⟩$ and $|1⟩$ states. However, measuring a qubit in superposition forces it to collapse into one of the basis states (e.g., $|0⟩$ or $|1⟩$). The outcome is probabilistic; you get a definite "yes" or "no" for a specific state, never a "maybe" or a percentage. Crucially, after measurement, the qubit is in the measured state, so subsequent identical measurements yield the same result, offering no new information. While a single measurement's outcome is unpredictable, its probability can be calculated. This unique nature limits single-qubit information capacity but also enables novel system designs.
For example, a photon's polarization can store a bit (e.g., horizontal for $|0⟩$, vertical for $|1⟩$). A recipient (Bob) measures a specific polarization, getting a "yes"/"no" answer. If the sender (Alice) sends an arbitrarily polarized photon, Bob’s measurement is probabilistic, and the photon’s state changes to reflect the measurement outcome. Copying a qubit by measuring and recreating isn't possible due to this measurement disturbance.

• Core: Qubits can exist in a combination of states simultaneously.
• Measurement Property: Measurement yields a probabilistic, definite outcome, collapsing the superposition and altering the qubit's state. Exact superposition ratios cannot be known, and qubits cannot be perfectly copied via measurement.

Entanglement:
Two or more qubits can be entangled. In this state, they share a linked fate: their properties are correlated even when physically separated. Measuring one entangled qubit instantaneously influences the state of the other(s), regardless of distance.

• Core: A strong, non-classical correlation between multiple qubits, where measuring one instantaneously affects others, even at a distance.

Note:
Importantly, if qubits are prepared independently (no entanglement) and restricted to basis states (no superposition), they behave like classical Boolean bits.

• Summary: Under specific conditions, qubits can mimic classical bits.

量子比特（qubit）是能存储单个比特但受量子力学限制的微小物理模型，其两个基本状态通常表示为 $|0⟩$ 和 $|1⟩$。与经典布尔比特相比，量子比特或其集合具有三个显著特性：可逆性、叠加态和纠缠态。

• 核心: 基于量子力学原理的比特，用 $|0⟩$ 和 $|1⟩$ 表示。
• 特性: 可逆性、叠加态、纠缠态使其区别于经典比特。

可逆性 (Reversibility):
量子系统的状态演化是可逆的，因此量子运算函数也是可逆的，输出不能被丢弃。但量子系统与环境相互作用导致信息丢失，以及测量行为本身，是不可逆性的两个重要来源。

• 核心: 量子操作原则上可逆。
• 例外: 与环境交互和测量过程引入不可逆性。

叠加态 (Superposition):
量子比特可以处于 $|0⟩$ 和 $|1⟩$ 的某种组合（叠加态）中。然而，对量子比特进行测量时，它会塌缩到被测量的特定状态（例如，问“是否为$|1⟩$?”，答案总是“是”或“否”，而不是概率分布）。测量结果是概率性的，且测量后量子比特的状态会改变为测量结果对应的状态，后续测量不会提供更多信息。因此，无法精确知道叠加的具体组合，也无法通过多次测量求平均或复制量子比特来获取更多信息。
以光子偏振为例：Alice可以用水平偏振代表$|0⟩$，垂直偏振代表$|1⟩$。Bob测量时只能选择一个特定方向问“是否是这个方向偏振？”，得到“是”或“否”的单一比特结果。如果Alice发送的是任意角度偏振的光子，Bob的测量结果是概率性的（概率与实际偏振方向和测量方向夹角的余弦平方有关），且测量后光子偏振方向会变为Bob测量的方向或其垂直方向。

• 核心: 量子比特可同时处于多种状态的组合。
• 测量特性: 测量会迫使量子比特选择一个确定状态（概率性选择），并改变其原有状态。无法精确得知叠加比例，也无法复制。

纠缠态 (Entanglement):
两个或多个量子比特可以被制备成一种特殊关联状态，即使它们物理上分离遥远，其状态仍然是相互关联的。对其中一个量子比特的测量结果会瞬间影响到其他纠缠量子比特的状态。

• 核心: 多个量子比特间存在一种超越经典认知的强关联，即使分离遥远，测量一个会影响其他。

注意:
如果量子系统被独立制备（无纠缠）且其状态被限制在如水平和垂直偏振（无叠加），那么量子比特的行为就如同经典的布尔比特。

• 总结: 在特定条件下，量子比特可以表现得像经典比特。

1.6 The Classical Bit

Unlike quantum bits (qubits) which are altered by measurement, classical bits can be measured repeatedly without being disturbed. This is possible because a classical bit is typically represented by a large number of identical physical objects (e.g., ~60,000 electrons for a single bit in semiconductor memory, or many photons in radio communication).

Because many objects are involved, measurements can yield a continuous range of values (like voltage from 0V to 1V), not just a binary "yes" or "no." This allows for error margins: specific voltage ranges (e.g., 0-0.2V for logical 0, 0.8-1V for logical 1) define the bit's state, with an undefined region in between.
A key mechanism is "restoring logic," where circuits actively correct small deviations from the ideal 0V and 1V values as information is processed. This ensures the robustness of modern computers.

Therefore, a classical bit is an abstraction: it's a model where a bit can be measured without perturbation, and as a result, copies of it can be made. This model works very well for circuits employing restoring logic.

While all physical systems are ultimately governed by quantum mechanics, the classical bit is an excellent approximation for current technology. However, as technology advances and components shrink to the scale of a few atoms or photons, the limiting role of quantum mechanics will become critical, and this classical approximation will eventually break down.

In essence:

• Classical bits are robust and can be repeatedly measured and copied because they are realized by many physical entities.
• Restoring logic is crucial for maintaining signal integrity despite noise.
• It's an approximation of quantum reality that holds well for current technology but will face limits as devices shrink.

与量子比特测量后会改变其状态不同，经典比特可以被重复测量而不会受到扰动。这是因为经典比特通常由大量具有相同属性的物理对象来表示（例如，半导体存储器中的一个比特可能由约6万个电子表示，或者无线电通信中使用大量光子）。

由于涉及大量对象，对其测量结果可以是一个连续的值（例如 $0V$ 到 $1V$ 的电压），而不仅仅是“是”或“否”的二元结果。这允许设定容错区间（error margins）：特定电压范围（如 $0-0.2V$ 代表逻辑 $0$ ， $0.8-1V$ 代表逻辑 $1$ ）定义比特状态，中间区域则不确定。
一种关键机制是 “恢复逻辑”（restoring logic），电路在信息处理过程中会主动纠正与理想 $0V$ 和 $1V$ 之间的微小电压偏差。这确保了现代计算机的鲁棒性（robustness）。

因此，经典比特是一个抽象概念：它是一个可以被测量而不受扰动的模型，因此可以被复制。这个模型非常适用于使用恢复逻辑的电路。

尽管所有物理系统最终都遵循量子力学，但经典比特对于当前技术而言是一个极佳的近似。然而，随着技术进步，当组件尺寸缩小到少量原子或光子级别时，量子力学的限制作用将变得至关重要，这种经典近似最终会失效。

简而言之：

• 经典比特因由大量物理实体实现而具有鲁棒性，可以被重复测量和复制。
• “恢复逻辑”对于抵抗噪声、维持信号完整性至关重要。
• 它是量子现实的一种近似，目前适用性良好，但随着器件微型化将面临量子效应的挑战。

Chapter 2: Codes

In the previous chapter, we examined the fundamental unit of information, the bit, and its various abstract representations. This chapter concerns ways in which complex objects can be represented not by a single bit, but by arrays of bits.
A simple communication system model includes: Input (Symbols) -> Coder -> Channel (Arrays of Bits) -> Decoder -> Output (Symbols). This chapter will look into several aspects of the design of codes.

上一章我们探讨了信息的基本单位——比特，以及其各种抽象表示。本章关注如何用比特的数组来表示复杂的对象，而非单个比特。
一个简单的通信系统模型包括：输入（符号）-> 编码器 -> 信道（比特数组）-> 解码器 -> 输出（符号）。本章将探讨代码设计的几个方面。

Some objects for which codes may be needed include:

• Letters: BCD, EBCDIC, ASCII, Unicode, Morse Code
• Integers: Binary, Gray, 2’s complement
• Numbers: Floating-Point
• Proteins: Genetic Code
• Telephones: NANP, International codes
• Hosts: Ethernet, IP Addresses, Domain names
• Images: TIFF, GIF, and JPEG
• Audio: MP3
• Video: MPEG

一些需要编码的对象包括：

• 字符: BCD, EBCDIC, ASCII, Unicode, 摩尔斯电码
• 整数: 二进制, 格雷码, 二进制补码
• 数字: 浮点数
• 蛋白质: 遗传密码
• 电话: NANP, 国际代码
• 主机: 以太网, IP地址, 域名
• 图像: TIFF, GIF, JPEG
• 音频: MP3
• 视频: MPEG

2.1 Symbol Space Size (符号空间大小)

Core Point: The number of symbols to be encoded (symbol space size) dictates the number of bits required and introduces different encoding challenges.

• 2 symbols: 1 bit is sufficient (e.g., coin toss).
• Integral power of 2 symbols: The number of bits required equals the logarithm, base 2, of the symbol space size (e.g., 4 card suits need 2 bits, 32 students need 5 bits).
• Finite but not integral power of 2 symbols: Use bits for the next higher power of 2, resulting in unused bit patterns (spare capacity), which is a key design issue (e.g., 10 digits need 4 bits, leaving 6 unused patterns).
• Infinite, countable symbols: Fixed-length bit strings can only represent a finite subset, leading to overflow for numbers outside the range (e.g., a 4-bit code for 0-15).
• Infinite, uncountable symbols: Requires discretization to approximate continuous values with a finite set of selected values. This approximation is irreversible, but can be sufficiently accurate with enough bits (e.g., Floating-Point representation of real numbers).

核心要点: 需要编码的符号数量（符号空间大小）决定了所需比特的数量，并引出不同的编码挑战。

• 符号数量为2: 1比特即可编码（如硬币正反）。
• 符号数量为2的整数次幂: 所需比特数等于符号空间大小的以2为底的对数（如4种花色需2比特，32名学生需5比特）。
• 符号数量有限但非2的整数次幂: 使用能覆盖其数量的最小2的幂的比特数，会产生未使用的比特模式（空闲容量），如何处理是设计关键（如10个数字需4比特，有6个未用模式）。
• 符号数量无限但可数: 固定长度的比特串只能表示有限范围内的符号，超出范围则出现**溢出(overflow)**情况，需特殊处理（如4比特只能表示0-15）。
• 符号数量无限且不可数: 必须进行离散化(discretization)，将连续值近似为有限个离散值。这种近似是不可逆的，但若比特数足够多，可实现足够精确的表示（如浮点数表示实数）。

2.2 Use of Spare Capacity (空闲容量的使用)

Core Point: In many situations, there are some unused code patterns because the number of symbols is not an integral power of 2. Handling these patterns is an important design issue.

• Strategies: Ignore, Map to other values, Reserve for future expansion, Use for control codes, Use for common abbreviations.

核心要点: 当符号数量不是2的整数次幂时，会出现未使用的代码模式（空闲容量），处理这些模式是代码设计的重要环节。

• 策略: 忽略、映射到其他有效值、保留以供未来扩展、用作控制代码、用作常用缩写。

2.2.1 Binary Coded Decimal (BCD) (二进制编码的十进制)

• Core: BCD uses ten four-bit patterns to represent digits 0-9, leaving six unused patterns (e.g., 1010).

• Handling: These unused patterns can either be ignored (signaling an error if encountered) or mapped into legal values (e.g., converting all to 9).

• 重点: BCD 用4比特表示0-9的十个数字，留下6个未使用的模式（例如1010）。

• 处理方式: 这些未使用的模式可以被忽略（遇到则报错）或映射到现有合法值（如全部映射为9）。

2.2.2 Genetic Code (遗传密码)

• Core: The Genetic Code is a biological encoding system that maps nucleotide sequences to amino acids, serving as a prime example of utilizing spare capacity and control codes.

• Encoding: DNA and RNA are made of four nucleotide bases (A, C, G, T/U). A sequence of three nucleotides (a "codon") is needed to encode 20 different amino acids (4^3 = 64 codons, far more than 20 needed).

• Utilization of Spare Capacity:

  • Redundancy/Robustness: Most amino acids are specified by more than one codon (e.g., Alanine has 4 codes starting with GC, meaning the third nucleotide can vary without changing the amino acid – this is called "wobble"). This provides biological robustness.
  • Control Codes: Three codons (UAA, UAG, UGA) serve as stop codes to terminate protein production. One codon (AUG) specifies Methionine and also acts as the start code, initiating protein synthesis.

• Significance: The Genetic Code illustrates how redundancy can enhance code robustness and how reserved bit sequences can function as control information.

• 核心: 遗传密码是生物学中的一种编码，将核苷酸序列映射为氨基酸，是利用空闲容量和控制码的典范。

• 编码方式: DNA和RNA由四种核苷酸（碱基：A, C, G, T/U）组成。需要3个核苷酸序列（称为“密码子”，codon）来编码20种不同的氨基酸（4^3 = 64种密码子，远超20种需求）。

• 空闲容量利用:

  • 冗余/健壮性: 大多数氨基酸由多个密码子编码（例如，丙氨酸有4个密码子，都以GC开头，这意味着第三个核苷酸的变化不会影响氨基酸种类，这被称为“摆动效应”(wobble)）。这提供了生物功能的鲁棒性。
  • 控制码: 三个密码子（UAA, UAG, UGA）被用作终止密码子 (stop code)，标志蛋白质合成的结束。一个密码子（AUG）既编码甲硫氨酸，也作为起始密码子 (start code)，标志蛋白质合成的开始。

• 重要性: 遗传密码展现了如何通过冗余来增强代码的鲁棒性，以及如何利用保留的比特序列作为控制信息。

2.2.3 Telephone Area Codes (电话区号)

• Core: Initial North American telephone Area Codes (1947) were designed with restrictions that limited them to 144 possible codes, with 58 reserved for future expansion.

• Future Expansion: These reserved codes sufficed for over four decades until 1995, when new Area Codes were created by relaxing the middle-digit restriction to meet the exploding demand for telephone network usage.

• 重点: 北美电话区号的设计初期（1947年）通过限制数字（首位非0/1，中间位0/1，后两位不同）只产生144个区号，其中58个保留用于未来扩展。

• 未来扩展: 这些预留的区号支撑了四十多年，直到1995年通过放宽中间位限制来创建新的区号，以应对电话网络使用爆炸式增长的需求。

2.2.4 IP Addresses (IP地址)

• Core: IPv4 addresses (32-bit) faced exhaustion due to the Internet's explosive growth.

• Future Expansion: IPv6 (128-bit) was developed with a vastly larger address space, including large blocks reserved for future expansion (humorously, some blocks are set aside for other planets).

• 重点: IPv4地址（32比特）因互联网的爆炸式增长面临耗尽。

• 未来扩展: IPv6（128比特）被开发出来，它包含巨大的地址空间，其中大块地址保留用于未来扩展（甚至有幽默说法称有为其他行星保留的地址）。

2.2.5 ASCII (美国信息交换标准代码)

• Core: ASCII (American Standard Code for Information Interchange) is a 7-bit code.

• Spare Capacity Use: Of its 128 codes, 33 are explicitly reserved as control characters (e.g., CR, LF), with only 95 for printable characters.

• 重点: ASCII (American Standard Code for Information Interchange) 是7比特代码。

• 空闲容量利用: 128个代码中有33个显式保留为控制字符（如回车CR、换行LF），只有95个用于可打印字符。

2.3 Extension of Codes (代码的扩展性)

Core Point: Codes are often designed by humans, and sometimes, their initial design biases lead to difficulties when extended for purposes not originally envisioned.

• Examples: ASCII's NUL (0000000) and DEL (1111111) were initially intended to be ignored, but their varying treatment across different systems (e.g., Unix) caused compatibility issues.
• Serious Bias: The use of CR (carriage return) and LF (line feed) in ASCII, originally tied to teletype machine physical operations, resulted in severe file format incompatibilities across operating systems (Unix uses LF, Macs use CR, DOS/Windows requires both), a persistent source of frustration and errors.

核心要点: 代码设计者在最初可能未能预见其未来用途，导致代码扩展时出现问题和意外的偏见。

• 例子: ASCII的NUL (0000000) 和DEL (1111111) 最初被设计为可忽略字符，但在不同系统（如Unix）中处理方式不同，导致兼容性问题。
• 严重偏见: ASCII中CR (回车) 和LF (换行) 的使用，原本对应电传打字机物理操作，但在不同操作系统中（Unix用LF，Mac用CR，Windows用CR+LF）导致了文件格式的严重不兼容，是持续的痛点。

2.4 Fixed-Length and Variable-Length Codes (定长码和变长码)

Core Point: A key decision in code design is whether to represent all symbols with codes of the same number of bits (fixed-length) or to allow some symbols to use shorter codes than others (variable-length).

• Fixed-length codes:
  • Advantages: Usually easier to deal with because both the coder and decoder know the number of bits in advance.
  • Transmission: Can be supported by parallel transmission. For serial transport, "framing errors" are a concern, often eliminated by sending "stop bits" between symbols to aid resynchronization.
• Variable-length codes:
  • Advantages: Can assign shorter codes to more frequent symbols, improving transmission efficiency.
  • Disadvantages: The decoder needs a way to determine when the code for one symbol ends and the next one begins (e.g., by noting time intervals).

核心要点: 编码设计初期需决定所有符号使用相同比特数（定长码）还是不同比特数（变长码）。

• 定长码:
  • 优点: 编解码器预先知道比特数，处理简单。
  • 传输: 可并行传输。串行传输时需解决“帧错误”(framing error)问题，常通过发送“停止位”(stop bits)来帮助同步。
• 变长码:
  • 优点: 可以给常用符号分配更短的代码，提高传输效率。
  • 缺点: 解码器需要额外机制来判断一个符号的代码何时结束，下一个符号何时开始（如通过时间间隔）。

2.4.1 Morse Code (摩尔斯电码)

• Core: Morse Code is a classic example of a variable-length code, developed for the telegraph.

• Encoding Principle: It uses sequences of short and long pulses or tones (dots and dashes) separated by short periods of silence. The decoder determines the end of a character's code by noting the length of silence before the next dot or dash (intra-character, inter-character, and inter-word separations have different lengths).

• Efficiency: Morse realized that some letters in the English alphabet are more frequently used than others, and he assigned them shorter codes. This allowed messages to be transmitted faster on average. He reportedly determined letter frequencies by counting movable type pieces in a print shop.

• Applications: Widely used for telegraphy and later in radio communications before voice transmission was common. It was a required communication mode for ocean vessels until 1999.

• 核心: 摩尔斯电码是变长码的经典例子，为电报发明。

• 编码原理: 使用短促的“点”和较长的“划”组成，通过它们之间不同长度的静默间隔来区分字符内部和字符之间、单词之间的界限。

• 效率: 摩尔斯意识到英文字母的使用频率不同，因此为高频字母分配更短的代码，从而平均加快了消息传输速度。据说他通过统计印刷厂铅字数量来确定字母频率。

• 应用: 广泛用于电报和早期的无线电通信。直到1999年，仍是远洋船舶的强制通信模式。

2.5 Detail: ASCII (美国信息交换标准代码)

• Standard: Introduced by ANSI in 1963, ASCII is a 7-bit code representing 33 control characters and 95 printing characters.

• 8-bit Extensions: In an 8-bit context, ASCII characters follow a leading 0. The 128 characters from HEX 80 to HEX FF (often called "extended ASCII") have been defined differently in various contexts (e.g., IBM PCs, Macs).

  • ISO-8859-1 (ISO-Latin), common for web pages, uses HEX A0-FF for Western European letters and punctuation, reserving HEX 80-9F as control characters.
  • Microsoft's Windows Code Page 1252 (Latin I) is similar but reassigns 27 of these 32 control codes to printed characters (e.g., HEX 80 for the Euro symbol), creating compatibility issues across platforms.

• Beyond 8-bits: To represent Asian languages and more, additional characters are needed. Unicode is the strongest candidate for a 2-byte (16-bit) standard character code, aiming to represent less than 65,536 different characters globally.

• 标准: 1963年引入的7比特代码，包含33个控制字符和95个可打印字符。

• 8比特扩展: 在8比特环境中，ASCII被视为“下半部分”。HEX 80到HEX FF之间的128个字符（常被称为“扩展ASCII”）在不同操作系统（如IBM PC、Mac）中有不同定义。

  • ISO-8859-1 (ISO-Latin) 是Web页面常用的8比特扩展，将HEX A0-FF用于西欧字符，将HEX 80-9F保留为控制字符。
  • 微软的Windows Code Page 1252 (Latin I) 则将ISO-8859-1中部分控制码（HEX 80-9F）重新分配给打印字符（如欧元符号），导致进一步的兼容性挑战。

• 超越8比特: 为表示亚洲语言等更多字符，需要更多比特。Unicode是目前最有力的16比特（2字节）字符编码标准，旨在支持全球范围内少于65,536个不同字符。

2.6 Detail: Integer Codes (整数编码)

Core Point: There are many ways to represent integers as bit patterns. All suffer from an inability to represent arbitrarily large integers in a fixed number of bits, potentially leading to an "overflow" condition.

• Binary Code:
  • Use: Nonnegative integers (e.g., memory addresses).
  • Property: For code of length n, the 2^n patterns represent integers 0 through 2^n - 1. The LSB (least significant bit) is 0 for even and 1 for odd integers.
• Binary Gray Code:
  • Use: Nonnegative integers, useful for sensors where the integer being encoded might change while a measurement is in progress.
  • Property: For code of length n, the 2^n patterns represent integers 0 through 2^n - 1. The two bit patterns of adjacent integers differ in exactly one bit.
• 2’s Complement:
  • Use: Both positive and negative integers, widely used for ordinary arithmetic in computers.
  • Property: For a code of length n, the 2^n patterns represent integers −2^(n-1) through 2^(n-1) - 1. The LSB is 0 for even and 1 for odd integers. Overlaps with binary code where applicable.
• Sign/Magnitude:
  • Use: Both positive and negative integers.
  • Property: For code of length n, the 2^n patterns represent integers −(2^(n-1) − 1) through 2^(n-1) − 1. The MSB (most significant bit) is 0 for positive and 1 for negative integers; the other bits carry the magnitude. Conceptually simple but awkward in practice, with separate representations for +0 and -0.
• 1’s Complement:
  • Use: Both positive and negative integers.
  • Property: For code of length n, the 2^n patterns represent integers −(2^(n-1) − 1) through 2^(n-1) − 1. The MSB is 0 for positive integers; negative integers are formed by complementing each bit of the corresponding positive integer. Awkward and rarely used today, with separate representations for +0 and -0.

核心要点: 整数有多种比特表示方式，它们都受限于固定比特数，可能导致“溢出”(overflow)条件。

• 二进制码 (Binary Code):
  • 用途: 非负整数 (如内存地址)。
  • 特性: n比特表示 0 到 2^n - 1。LSB (最低有效位) 决定奇偶。
• 二进制格雷码 (Binary Gray Code):
  • 用途: 非负整数，尤其适用于测量变化的物理量（如传感器）。
  • 特性: n比特表示 0 到 2^n - 1。相邻整数的比特模式只相差一位。
• 2的补码 (2’s Complement):
  • 用途: 有符号整数，广泛用于计算机普通算术。
  • 特性: n比特表示 -2^(n-1) 到 2^(n-1) - 1。LSB 决定奇偶。与二进制码重叠部分相同。
• 符号-幅度码 (Sign/Magnitude):
  • 用途: 有符号整数。
  • 特性: n比特表示 -(2^(n-1) − 1) 到 2^(n-1) − 1。MSB (最高有效位) 为0表示正，1表示负；其余位表示幅度。概念简单但实际操作不便，存在+0和-0两种表示。
• 1的补码 (1’s Complement):
  • 用途: 有符号整数。
  • 特性: n比特表示 -(2^(n-1) − 1) 到 2^(n-1) − 1。MSB为0表示正；负数通过对应正数每位取反得到。不常用且不便，存在+0和-0两种表示。
    原码、补码与反码 (Sign-Magnitude Representation, One's Complement and Two's Complement)

2.7 Detail: The Genetic Code (遗传密码的详细说明)

Core Point: The Genetic Code is a natural encoding system in living organisms used to translate genetic information (DNA/RNA) into proteins. It demonstrates redundancy and control mechanisms in code design.

核心要点: 遗传密码是生物体中用于将遗传信息（DNA/RNA）翻译成蛋白质的自然编码系统。它展示了编码设计中的冗余和控制机制。

• Information Flow: DNA (genes) → mRNA (messenger RNA) → Ribosome/tRNA → Protein. Proteins are fundamental structural and functional units of cells and organisms.

• 编码方式: DNA (基因) → mRNA (信使RNA) → 核糖体/tRNA → 蛋白质。蛋白质是细胞和有机体的基本组成和功能单位。

• Encoding Unit:

  • DNA and RNA are composed of four different nucleotide bases (A, C, G, T/U).
  • A triplet codon (three nucleotides) is required to encode the 20 different amino acids, resulting in 4^3 = 64 possible combinations.

• 编码单位:

  • DNA和RNA由四种不同的核苷酸（碱基：A, C, G, T/U）组成。
  • 编码20种氨基酸需要三联体密码子(codon)，共 4^3 = 64 种组合。

• Redundancy and Robustness:

  • Most amino acids are specified by more than one codon (e.g., Alanine has 4, Isoleucine has 3).
  • This redundancy enhances the code's robustness; even if a mutation occurs in the third nucleotide position, it may not change the encoded amino acid (known as the wobble effect).

• 冗余性与鲁棒性:

  • 大多数氨基酸有多个对应的密码子（例如，丙氨酸有4个，异亮氨酸有3个）。
  • 这种冗余增加了代码的健壮性，尤其是在第三个核苷酸位置，即使发生突变，也可能不会改变最终编码的氨基酸（称为摆动效应，wobble）。

• Control Information:

  • Start Codon: AUG codes for Methionine and also signals the beginning of protein synthesis.
  • Stop Codons: UAA, UAG, and UGA do not code for any amino acid; instead, they signify the end of the protein chain, as proteins vary in length.

• 控制信息:

  • 起始密码子: AUG 编码甲硫氨酸，并标志蛋白质合成的开始。
  • 终止密码子: UAA, UAG, UGA 不编码任何氨基酸，而是标志蛋白质合成的结束，因为蛋白质长度不同。

• Value: Although the coded description of a protein (DNA/RNA) may require more atoms than the protein itself, its standardized representation allows the same "assembly apparatus" (ribosome) to fabricate different proteins at different times, enabling versatility.

• 价值: 尽管蛋白质的编码描述（DNA/RNA）在原子数上可能比蛋白质本身更大，但其标准化表示使得同一个“组装设备”（核糖体）可以在不同时间制造不同的蛋白质，实现了通用性。

2.8 Detail: IP Addresses (IP地址的详细说明)

• Version 4 (IPv4): Each address is 32 bits, in the form x.x.x.x, where each x is a number between 0 and 255.

• 管理: IP地址由互联网号码分配机构 (IANA) 管理分配。

• Address Exhaustion & IPv6: Due to the Internet's explosive growth, IPv4 addresses faced exhaustion.

• 版本4 (IPv4): 每个地址由32比特组成，形式为x.x.x.x，每个x是0-255的数字。

• Management: IP addresses are assigned by the Internet Assigned Numbers Authority (IANA).

• 地址耗尽与IPv6: 随着互联网的爆炸性增长，IPv4地址面临耗尽。

• Version 6 (IPv6):

  • Design: Each address is expanded to 128 bits, dramatically increasing the address space.
  • Purpose: To accommodate unique addresses for a vast number of devices, including appliances and sensors in vehicles.
  • Strategy: New allocations include large blocks reserved for future expansion (humorously, some blocks are set aside for other planets).

• 版本6 (IPv6):

  • 设计: 每个地址扩展为128比特，极大地增加了地址空间。
  • 目的: 能够为更多设备（如家用电器、汽车中的传感器）分配独立地址。
  • 策略: 新的分配方案包含了大量为未来扩展而保留的地址块（甚至有幽默说法称有为其他行星保留的地址）。

2.9 Detail: Morse Code (摩尔斯电码的详细说明)

• Invention Context: Samuel F. B. Morse, motivated by his wife's sudden death and the inability to communicate rapidly, invented Morse Code.

• 发明背景: 塞缪尔·摩尔斯因妻子猝死未能及时赶回的经历，促使他意识到快速通信的重要性，从而发明了摩尔斯电码。

• Encoding Method:

  • A variable-length code consisting of short and long pulses or tones (dots and dashes) separated by short periods of silence.
  • If a dot's duration is one unit of time, a dash is three units. The space between dots and dashes within one character is one unit, between characters is three units, and between words is seven units.

• 编码方式:

  • 一种变长码，由短促的“点”和较长的“划”组成，通过不同长度的静默间隔区分字符和单词。
  • “点”的时长为1个时间单位，“划”为3个单位。字符内点划间间隔1单位，字符间间隔3单位，单词间间隔7单位。

• Design Advantage: Morse realized that some letters in the English alphabet are more frequently used than others, and he assigned them shorter codes. This allowed messages to be transmitted faster on average. He reportedly determined letter frequencies by counting movable type pieces in a print shop.

• 设计优点: 摩尔斯根据英文字母的使用频率为它们分配了不同的代码长度，高频字母（如E、T）拥有更短的代码，从而提高了平均传输速度。据说他通过统计印刷厂的铅字数量来确定字母频率。

• Applications: Widely used for telegraphy and later in radio communications before voice transmission was common. It remained a required communication mode for ocean vessels until 1999 and is still a requirement for some amateur radio licenses in the U.S.

• 应用: 广泛用于电报和早期的无线电通信。直到1999年，仍是远洋船舶的强制通信模式，在美国，某些业余无线电执照仍要求掌握摩尔斯电码。

Chapter 3: Compression (压缩)

In Chapter 1 we examined the fundamental unit of information, the bit, and its various abstract representations: the Boolean bit, the circuit bit, the control bit, the physical bit, the quantum bit, and the classical bit. Our never-ending quest for improvement made us want representations of single bits that are smaller, faster, stronger, smarter, safer, and cheaper.
In Chapter 2 we considered some of the issues surrounding the representation of complex objects by arrays of bits (at this point, Boolean bits). The mapping between the objects to be represented (the symbols) and the array of bits used for this purpose is known as a code. We naturally want codes that are stronger and smaller, i.e., that lead to representations of objects that are both smaller and less susceptible to errors.
In this chapter we will consider techniques of compression that can be used for generation of particularly efficient representations. In Chapter 4 we will look at techniques of avoiding errors.
In Chapter 2 we considered systems of the sort shown in Figure 3.1, in which symbols are encoded into bit strings, which are transported (in space and/or time) to a decoder, which then recreates the original symbols.

在第1章中，我们探讨了信息的基本单位——比特，以及其各种抽象表示：布尔比特、电路比特、控制比特、物理比特、量子比特和经典比特。我们对改进的不断追求使我们希望获得更小、更快、更强、更智能、更安全、更廉价的单比特表示。
在第2章中，我们讨论了用比特数组（此时是布尔比特）表示复杂对象的一些问题。待表示的对象（符号）与用于此目的的比特数组之间的映射被称为代码。我们自然希望代码更强、更小，即能使对象表示更小且不易出错的代码。
本章将探讨可用于生成特别高效表示的压缩技术。第4章中我们将研究避免错误的技术。
第2章中我们讨论了如图3.1所示的系统，其中符号被编码成比特串，然后（在空间和/或时间上）传输给解码器，解码器再重构出原始符号。

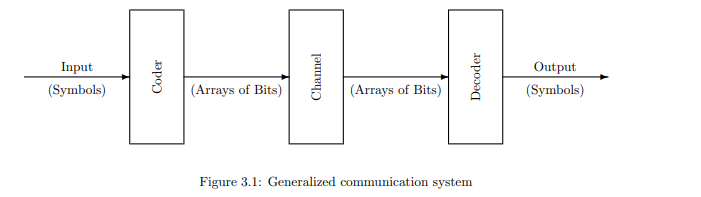
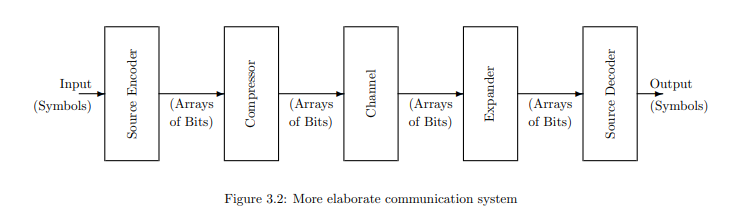
Typically the same code is used for a sequence of symbols, one after another. The role of data compression is to convert the string of bits representing a succession of symbols into a shorter string for more economical transmission, storage, or processing. The result is the system in Figure 3.2, with both a compressor and an expander. Ideally, the expander would exactly reverse the action of the compressor so that the coder and decoder could be unchanged.
On first thought, this approach might seem surprising. Why is there any reason to believe that the same information could be contained in a smaller number of bits? We will look at two types of compression, using different approaches:
• Lossless or reversible compression (which can only be done if the original code was inefficient, for example by having unused bit patterns, or by not taking advantage of the fact that some symbols are used more frequently than others)
• Lossy or irreversible compression, in which the original symbol, or its coded representation, cannot be reconstructed from the smaller version exactly, but instead the expander produces an approximation that is “good enough”
Six techniques are described below which are astonishingly effective in compressing data files. The first five are reversible, and the last one is irreversible. Each technique has some cases for which it is particularly well suited (the best cases) and others for which it is not well suited (the worst cases).

通常，同一个代码会用于一系列连续的符号。数据压缩的作用是将表示一系列符号的比特串转换为更短的字符串，以便更经济地传输、存储或处理。结果是图3.2所示的系统，其中包含压缩器和解压器。理想情况下，解压器会精确地逆转压缩器的操作，以便编码器和解码器可以保持不变。
乍一看，这种方法可能令人惊讶。为什么会有人认为相同的信息可以包含在更少数量的比特中呢？我们将探讨两种不同方法的压缩类型：

• 无损或可逆压缩（仅当原始代码效率低下时才能进行，例如存在未使用的比特模式，或未利用某些符号使用频率更高的事实）。
• 有损或不可逆压缩，其中原始符号或其编码表示无法从较小的版本中精确重建，而是由解压器产生一个“足够好”的近似值。
  下面将描述六种在压缩数据文件方面效果惊人的技术。前五种是可逆的，最后一种是不可逆的。每种技术都有其特别适用的情况（最佳情况）和不适用的情况（最差情况）。

3.1 Variable-Length Encoding (变长编码)

In Chapter 2 Morse code was discussed as an example of a source code in which more frequently occurring letters of the English alphabet were represented by shorter codewords, and less frequently occurring letters by longer codewords. On average, messages sent using these codewords are shorter than they would be if all codewords had the same length. Variable-length encoding can be done either in the source encoder or the compressor. A general procedure for variable-length encoding will be given in Chapter 5, so a discussion of this technique is put off until that chapter.

在第2章中，摩尔斯电码被讨论为一个源编码的例子，其中英文字母中出现频率较高的字母由较短的码字表示，而出现频率较低的字母由较长的码字表示。平均而言，使用这些码字发送的消息比所有码字长度相同的情况下要短。变长编码可以在源编码器或压缩器中完成。变长编码的一般过程将在第5章中给出，因此对该技术的讨论推迟到那一章。

• Core: Assigns shorter codewords to more frequently occurring symbols and longer codewords to less frequent ones, leading to shorter average message lengths.

• Distinction: Improves transmission efficiency compared to fixed-length encoding; implementation details deferred to Chapter 5.

• 核心: 将较短的码字分配给出现频率较高的符号，将较长的码字分配给出现频率较低的符号，从而缩短平均消息长度。

• 区分: 相较于定长编码提高了传输效率；具体实现细节推迟到第5章讨论。

3.2 Run Length Encoding (行程长度编码)

Suppose a message consists of long sequences of a small number of symbols or characters. Then the message could be encoded as a list of the symbol and the number of times it occurs. For example, the message “a B B B B B a a a B B a a a a” could be encoded as “a 1 B 5 a 3 B 2 a 4”. This technique works very well for a relatively small number of circumstances. One example is the German flag, which could be encoded as so many black pixels, so many red pixels, and so many yellow pixels, with a great saving over specifying every pixel. Another example comes from fax technology, where a document is scanned and long groups of white (or black) pixels are transmitted as merely the number of such pixels (since there are only white and black pixels, it is not even necessary to specify the color since it can be assumed to be the other color).
Run length encoding does not work well for messages without repeated sequences of the same symbol. For example, it may work well for drawings and even black-and-white scanned images, but it does not work well for photographs since small changes in shading from one pixel to the next would require many symbols to be defined.

假设一条消息包含少量符号或字符的冗长序列。那么消息可以被编码为符号及其出现次数的列表。例如，消息“a B B B B B a a a B B a a a a”可以编码为“a 1 B 5 a 3 B 2 a 4”。这项技术在相对较少的情况下效果非常好。一个例子是德国国旗，可以编码为若干黑色像素、若干红色像素和若干黄色像素，相比逐一指定每个像素，能节省大量空间。另一个例子来自传真技术，其中文档被扫描后，长串的白色（或黑色）像素仅作为此类像素的数量进行传输（由于只有黑白像素，甚至无需指定颜色，因为它可被假定为另一种颜色）。
行程长度编码对于没有重复相同符号序列的消息效果不佳。例如，它可能适用于绘图甚至是黑白扫描图像，但对于照片效果不佳，因为从一个像素到下一个像素的微小阴影变化将需要定义许多符号。

• Core: Run length encoding (RLE) compresses data by replacing consecutive occurrences of the same data value with a count and the value itself.

• Distinction: Highly effective for data with long runs of identical symbols (e.g., simple graphics, fax lines), but inefficient for diverse data (e.g., photographs with gradual shading changes) as it may increase file size.

• 核心: 行程长度编码（RLE）通过将连续出现相同数据值的序列替换为该值和其出现次数来压缩数据。

• 区分: 对于具有长串相同符号的数据（例如，简单图形、传真线）非常有效，但对于多样化数据（例如，颜色渐变的照片）效率低下，甚至可能增加文件大小。

3.3 Static Dictionary (静态字典)

If a code has unused codewords, these may be assigned, as abbreviations, to frequently occurring sequences of symbols. Then such sequences could be encoded with no more bits than would be needed for a single symbol. For example, if English text is being encoded in ASCII and the DEL character is regarded as unnecessary, then it might make sense to assign its codeword 127 to the common word “the”. Practical codes offer numerous examples of this technique. The list of the codewords and their meanings is called a codebook, or dictionary. The compression technique considered here uses a dictionary which is static in the sense that it does not change from one message to the next.
An example will illustrate this technique. Before the the electric telegraph, there were other schemes for transmitting messages long distances. A mechanical telegraph described in some detail by Wilson1 was put in place in 1796 by the British Admiralty to communicate between its headquarters in London and various ports, including Plymouth, Yarmouth, and Deal. It consisted of a series of cabins, each within sight of the next one, with six large shutters which could rotated to be horizontal (open) or vertical (closed). See Figure 3.4. In operation, all shutters were in the open position until a message was to be sent. Then all shutters were closed to signal the start of a message (operators at the cabins were supposed to look for new messages every five minutes). Then the message was sent in a sequence of shutter patterns, ending with the all-open pattern.
There were six shutters, and therefore 64 (2^6) patterns. Two of these were control codes (all open was “start” and “stop,” and all closed was “idle”). The other 62 were available for 24 letters of the alphabet (26 if J and U were included, which was not essential because they were recent additions to the English alphabet), 10 digits, an end-of-word marker, and an end-of-page marker. This left over 20 unused patterns which were assigned to commonly occurring words or phrases. The particular abbreviations used varied from time to time, but included common words like “the”, locations such as “Portsmouth”, and other words of importance such as “French”, “Admiral”, “east”, and “frigate”. It also included phrases like “Commander of the West India Fleet” and “To sail, the first fair wind, to the southward”.
Perhaps the most intriguing entries in the codebook were “Court-Martial to sit” and “Sentence of court martial to be put into execution”. Were courts-martial really common enough and messages about them frequent enough to justify dedicating two out of 64 code patterns to them?
As this example shows, long messages can be shortened considerably with a set of well chosen abbreviations. However, there is an inherent risk: the effect of errors is apt to be much greater. If full text is transmitted, a single error causes a misspelling or at worst the wrong word, which humans can usually detect and correct. With abbreviations, a single incorrect bit could result in a possible but unintended meaning: “east” might be changed to “south”, or a single letter might be changed to “Sentence of court-martial to be put into execution” with significant consequences.
This telegraph system worked well. During one demonstration a message went from London to Plymouth and back, a distance of 500 miles, in three minutes. That’s 13 times the speed of sound.
If abbreviations are used to compress messages, there must be a codebook showing all the abbreviations in use, that is distributed before the first message is sent. Because it is distributed only once, the cost of distribution is low on a per-message basis. But it has to be carefully constructed to work with all messages expected, and cannot be changed to match the needs of individual messages.
This technique works well for sets of messages that are quite similar, as might have been the case with 18th-century naval communications. It is not well suited for more diverse messages. This mechanical telegraph was never adapted for commercial or public use, which would have given it more diverse set of messages without as many words or phrases in common.

如果一个代码有未使用的码字，这些码字可以作为缩写，分配给经常出现的符号序列。这样，这些序列就可以用不比单个符号所需更多的比特来编码。例如，如果英文文本正在用ASCII编码，而DEL字符被认为是多余的，那么将其码字127分配给常用词“the”可能是有意义的。实际代码提供了许多这种技术的例子。码字及其含义的列表称为码本或字典。这里考虑的压缩技术使用一个静态字典，即它不会从一条消息更改到下一条消息。
一个例子将说明这项技术。在电报出现之前，还有其他长距离传输消息的方案。威尔逊详细描述了一种机械电报，于1796年由英国海军部投入使用，用于伦敦总部与普利茅斯、雅茅斯和迪尔等港口之间的通信。它由一系列小屋组成，每个小屋都在下一个小屋的视线范围内，有六个大的百叶窗，可以旋转成水平（打开）或垂直（关闭）。参见图3.4。在操作中，所有百叶窗都处于打开位置，直到要发送消息。然后所有百叶窗都关闭以表示消息的开始信号（小屋的操作员每五分钟应检查是否有新消息）。然后消息以一系列百叶窗图案的形式发送，以全开图案结束。
有六个百叶窗，因此有64（2^6）种图案。其中两个是控制码（全开表示“开始”和“停止”，全关表示“空闲”）。其余62个可用于24个字母（如果包括J和U则是26个，这不是必需的，因为它们是英语字母表的新增字母）、10个数字、一个单词结束标记和一个页面结束标记。这留下了20多个未使用的图案，这些图案被分配给常用词或短语。使用的具体缩写不时变化，但包括“the”等常用词，如“Portsmouth”等地点，以及“French”、“Admiral”、“east”和“frigate”等重要词语。它还包括“Commander of the West India Fleet”和“To sail, the first fair wind, to the southward”等短语。
也许码本中最有趣的条目是“军事法庭开庭”和“军事法庭判决执行”。军事法庭真的足够常见，关于它们的消息也足够频繁，以至于在64个代码模式中专门分配两个给它们吗？
正如这个例子所示，通过一组精心选择的缩写，长消息可以大大缩短。然而，存在固有的风险：错误的影响可能会大得多。如果传输的是完整文本，单个错误会导致拼写错误或最坏情况下的错误词语，人类通常可以检测和纠正。使用缩写时，单个错误的比特可能导致一种可能但非预期的含义：“east”可能被改为“south”，或者单个字母可能被改为“军事法庭判决执行”，带来重大后果。
这种电报系统运行良好。在一次演示中，一条消息从伦敦到普利茅斯再返回，距离500英里，只用了三分钟。那是音速的13倍。
如果使用缩写来压缩消息，则必须有一个码本，显示所有正在使用的缩写，并在第一条消息发送之前分发。由于只分发一次，因此每条消息的成本较低。但它必须精心构建以适用于所有预期消息，并且不能根据单个消息的需求进行更改。
这种技术非常适用于相当相似的消息集，就像18世纪海军通信的情况。它不适用于更多样化的消息。这种机械电报从未适应商业或公共用途，那将使其拥有更多样化的消息集，而没有那么多常用词或短语。

• Core: Assigns fixed abbreviations (codewords) from a predefined, unchanging dictionary to frequently occurring symbol sequences, utilizing unused code patterns.

• Distinction: Effective for sets of messages that are very similar (high repetition of specific words/phrases); high risk of severe error impact (a single bit error can drastically change meaning); dictionary must be constructed carefully beforehand and cannot adapt to individual messages.

• 核心: 将预定义、不变字典中的固定缩写（码字）分配给经常出现的符号序列，从而利用未使用的代码模式进行压缩。

• 区分: 对非常相似的消息集（特定词语/短语重复率高）有效；错误影响风险高（单个比特错误可能彻底改变含义）；字典必须预先精心构建，且无法根据单个消息的需求改变。

3.4 Semi-adaptive Dictionary (半自适应字典)

The static-dictionary approach requires one dictionary, defined in advance, that applies to all messages. If a new dictionary could be defined for each message, the compression could be greater because the particular sequences of symbols found in the message could be made into dictionary entries.
Doing so would have several drawbacks, however. First, the new dictionary would have to be transmitted along with the encoded message, resulting in increased overhead. Second, the message would have to be analyzed to discover the best set of dictionary entries, and therefore the entire message would have to be available for analysis before any part of it could be encoded (that is, this technique has large latency). Third, the computer calculating the dictionary would need to have enough memory to store the entire message.
These disadvantages have limited the use of semi-adaptive dictionary compression schemes.

静态字典方法需要一个预先定义好的字典，该字典适用于所有消息。如果能为每条消息定义一个新字典，则压缩效果会更好，因为消息中发现的特定符号序列可以被制成字典条目。
然而，这样做有几个缺点。首先，新字典必须与编码消息一起传输，从而增加了开销。其次，必须分析消息以发现最佳字典条目集，因此在编码任何部分之前，整个消息都必须可供分析（即，这项技术具有大的延迟）。第三，计算字典的计算机需要有足够的内存来存储整个消息。
这些缺点限制了半自适应字典压缩方案的利用。

• Core: A dictionary is created for each individual message, allowing for potentially higher compression by optimizing dictionary entries for specific message content.

• Distinction: Faces significant practical drawbacks including increased overhead due to dictionary transmission, high latency (requiring full message analysis before encoding), and high memory requirements for dictionary calculation, thus limiting its widespread use.

• 核心: 为每条独立消息创建新字典，通过针对特定消息内容优化字典条目，可能实现更高的压缩率。

• 区分: 面临显著的实际缺点，包括因字典传输而增加开销、高延迟（编码前需分析整个消息）和字典计算所需的高内存，因此限制了其广泛应用。

3.5 Dynamic Dictionary (动态字典)

What would be best for many applications would be an encoding scheme using a dictionary that is calculated on the fly, as the message is processed, does not need to accompany the message, and can be used before the end of the message has been processed. On first consideration, this might seem impossible. However, such a scheme is known and in wide use. It is the LZW compression technique, named after Abraham Lempel, Jacob Ziv, and Terry Welch. Lempel and Ziv actually had a series of techniques, sometimes referred to as LZ77 and LZ78, but the modification by Welch in 1984 gave the technique all the desired characteristics.
Welch wanted to reduce the number of bits sent to a recording head in disk drives, partly to increase the effective capacity of the disks, and partly to improve the speed of transmission of data. His scheme is described here, for both the encoder and decoder. It has been widely used, in many contexts, to lead to reversible compression of data. When applied to text files on a typical computer, the encoded files are typically half the size of the original ones. It is used in popular compression products such as Stuffit or Disk Doubler. When used on color images of drawings, with large areas that are the exact same color, it can lead to files that are smaller than half the size compared with file formats in which each pixel is stored. The commonly used GIF image format uses LZW compression. When used with photographs, with their gradual changes of color, the savings are much more modest.
Because this is a reversible compression technique, the original data can be reconstructed exactly, without approximation, by the decoder.
The LZW technique seems to have many advantages. However, it had one major disadvantage. It was not freely available—it was patented. The U.S. patent, No. 4,558,302, expired June 20, 2003, and patents in other countries in June, 2004, but before it did, it generated a controversy that is still an unpleasant memory for many because of the way it was handled.

对于许多应用而言，最佳方案是一种使用动态字典的编码方案，该字典在消息处理过程中实时计算，无需随消息传输，并且可以在消息处理结束前使用。乍一看，这似乎不可能。然而，这种方案是已知的，并且被广泛使用。它就是 LZW 压缩技术，以亚伯拉罕·莱佩尔（Abraham Lempel）、雅各布·齐夫（Jacob Ziv）和特里·韦尔奇（Terry Welch）的名字命名。莱佩尔和齐夫实际上有一系列技术，有时被称为LZ77和LZ78，但韦尔奇在1984年的修改赋予了该技术所有期望的特性。
韦尔奇希望减少发送到磁盘驱动器磁头的数据位数，部分是为了增加磁盘的有效容量，部分是为了提高数据传输速度。他的方案在这里为编码器和解码器都进行了描述。它在许多情况下被广泛使用，可实现数据的可逆压缩。当应用于典型计算机上的文本文件时，编码后的文件通常是原始文件大小的一半。它被Stuffit或Disk Doubler等流行压缩产品使用。当用于具有大面积相同颜色的彩色绘图图像时，生成的文件可以比每个像素单独存储的文件格式小一半以上。常用的GIF图像格式就使用LZW压缩。当用于颜色渐变的照片时，节省的空间则要小得多。
由于这是一种可逆压缩技术，原始数据可以由解码器精确重建，没有任何近似。
LZW技术似乎有很多优点。然而，它有一个主要缺点：它并非免费可用——它被授予了专利。美国专利号4,558,302于2003年6月20日到期，其他国家的专利于2004年6月到期，但在到期之前，它引发了一场争议，因其处理方式至今仍令许多人记忆不佳。

• Core: LZW (Lempel-Ziv-Welch) compression builds its dictionary dynamically during processing (on-the-fly), eliminating the need for pre-transmission or full message analysis, enabling highly efficient reversible compression.

• Distinction: Widely used and very effective for text files and images with large uniform color areas (e.g., GIF); less effective for photographs with gradual changes; controversially patented for many years, leading to the development of alternative formats like PNG.

• 核心: LZW（Lempel-Ziv-Welch）压缩在处理过程中动态（实时）构建字典，无需预先传输或对整个消息进行分析，实现了高效的可逆压缩。

• 区分: 被广泛使用，对文本文件和具有大面积均匀颜色的图像（例如GIF）非常有效；对颜色渐变的照片效果较差；多年来因专利问题备受争议，导致了PNG等替代格式的开发。

3.5.1 The LZW Patent (LZW专利)

Welch worked for Sperry Research Center at the time he developed his technique, and he published a paper2 describing the technique. Its advantages were quickly recognized, and it was used in a variety of compression schemes, including the Graphics Interchange Format GIF developed in 1987 by CompuServe (a national Internet Service Provider) for the purpose of reducing the size of image files in their computers. Those who defined GIF did not realize that the LZW algorithm, on which GIF was based, was patented. The article by Welch did not warn that a patent was pending. The World Wide Web came into prominence during the early 1990s, and the first graphical browsers accepted GIF images. Consequently, Web site developers routinely used GIF images, thinking the technology was in the public domain, which had been CompuServe’s intention.
By 1994, Unisys, the successor company to Sperry, realized the value of this patent, and decided to try to make money from it. They approached CompuServe, who didn’t pay much attention at first, apparently not thinking that the threat was real. Finally, CompuServe took Unisys seriously, and the two companies together announced on December 24, 1994, that any developers writing software that creates or reads GIF images would have to license the technology from Unisys. Web site developers were not sure if their use of GIF images made them responsible for paying royalties, and they were not amused at the thought of paying for every GIF image on their sites. Soon Unisys saw that there was a public-relations disaster in the making, and they backed off on their demands. On January 27, 1995, they announced they would not try to collect for use of existing images or for images produced by tools distributed before the end of 1994, but did insist on licensing graphics tools starting in 1995. Images produced by licensed tools would be allowed on the Web without additional payment.
In 1999, Unisys decided to collect from individual Web sites that might contain images from unlicensed tools, at the rate of $5000 per site, with no exception for nonprofits, and no smaller license fees for small, low-traffic sites. It is not known how many Web sites actually paid that amount; it is reported that in the first eight months only one did. The feeling among many Web site developers was one of frustration and anger. Although Unisys avoided a public-relations disaster in 1995, they had one on their hands in 1999.
There were very real cultural differences between the free-wheeling Web community, often willing to share freely, and the business community, whose standard practices were designed to help make money.
A non-infringing public-domain image-compression standard called PNG was created to replace GIF, but the browser manufacturers were slow to adopt yet another image format. Also, everybody knew that the patents would expire soon. The controversy has now gone away except in the memory of a few who felt particularly strongly. It is still cited as justification for or against changes in the patent system, or even the concept of software patents in general.
As for PNG, it offers some technical advantages (particularly better transparency features) and, as of 2004, was well supported by almost all browsers, the most significant exception being Microsoft Internet Explorer for Windows.

韦尔奇在开发其技术时在Sperry研究中心工作，并发表了一篇描述该技术的论文。其优势很快得到认可，并被用于各种压缩方案，包括1987年由CompuServe（一家全国性互联网服务提供商）开发的图形交换格式GIF，旨在减小其计算机中图像文件的大小。定义GIF的人并未意识到GIF所基于的LZW算法已获得专利。韦尔奇的文章并未警告专利正在申请中。万维网在20世纪90年代初崭露头角，第一批图形浏览器支持GIF图像。因此，网站开发者常规使用GIF图像，认为该技术属于公共领域，而这也是CompuServe的初衷。
到1994年，Sperry的继任公司Unisys意识到这项专利的价值，并决定从中获利。他们联系了CompuServe，后者起初并未太在意，显然认为威胁并非真实。最终，CompuServe认真对待Unisys，两家公司于1994年12月24日共同宣布，任何编写创建或读取GIF图像软件的开发者都必须从Unisys获得该技术的许可。网站开发者不确定他们使用GIF图像是否需要支付版税，并且对于为他们网站上的每个GIF图像付费感到不悦。很快，Unisys意识到一场公关灾难正在酝酿中，他们便放弃了部分要求。1995年1月27日，他们宣布不会对现有图像或1994年底之前分发的工具生产的图像收取费用，但坚持要求从1995年开始对图形工具进行许可。经许可工具生产的图像将被允许在网络上使用，无需额外付费。
1999年，Unisys决定向可能包含未经许可工具制作图像的独立网站收取费用，每站5000美元，非营利组织不例外，小流量网站也没有更低的许可费。目前尚不清楚实际有多少网站支付了这笔费用；据报道，前八个月只有一个网站支付了。许多网站开发者感到沮丧和愤怒。尽管Unisys在1995年避免了一场公关灾难，但在1999年却遭遇了。
自由奔放的网络社区（通常乐于自由分享）与商业社区（其标准做法旨在赚钱）之间存在着非常真实的文化差异。
一种不侵权的公共领域图像压缩标准PNG被创建出来以取代GIF，但浏览器制造商在采用另一种图像格式方面进展缓慢。此外，每个人都知道专利很快就会到期。这场争议现在已经平息，除了少数对此感受特别强烈的人记忆犹新。它仍然被引用为支持或反对专利制度，甚至是软件专利概念的理由。
至于PNG，它提供了一些技术优势（特别是更好的透明度功能），并且截至2004年，几乎所有浏览器都对其提供了良好支持，最显著的例外是Windows版Microsoft Internet Explorer。

• Core: The LZW algorithm, foundational to the GIF image format, was patented by Unisys, leading to significant controversy and licensing disputes after its value was recognized.

• Distinction: The patent controversy alienated the free-sharing Web community, prompted the development of the non-infringing PNG format, and highlighted cultural clashes between open-source principles and business practices. The patents expired in 2003/2004.

• 核心: LZW算法是GIF图像格式的基础，其专利权归Unisys所有，在专利价值被认可后引发了重大争议和许可纠纷。

• 区分: 专利争议疏远了自由分享的网络社区，促使了非侵权PNG格式的开发，并凸显了开源原则与商业实践之间的文化冲突。相关专利已于2003/2004年到期。

3.5.2 How does LZW work? (LZW工作原理?)

The technique, for both encoding and decoding, is illustrated with a text example in Section 3.7.

编码和解码技术都将在3.7节中通过一个文本示例进行说明。

• Core: (No new information provided in this subsection, directs to Section 3.7 for details).

• Distinction: (No new information provided in this subsection).

• 核心: (本小节未提供新信息，指引至3.7节查看详情)。

• 区分: (本小节未提供新信息)。

3.6 Irreversible Techniques (不可逆技术)

Irreversible (lossy) compression permanently discards some data from the original message. This is acceptable for applications where perfect reconstruction is not required, especially when the discarded information is imperceptible or less relevant to human senses. The goal is to achieve significantly higher compression ratios by making "good enough" approximations, often by exploiting the limitations of human perception.

• Core: Permanently discards some original data for significantly higher compression ratios.
• Distinction: Relies on perceptual limitations (e.g., human sight/hearing) to determine what information can be safely removed; unlike lossless compression, original data cannot be perfectly reconstructed.

不可逆（有损）压缩会永久性地丢弃原始消息中的部分数据。这对于不需要完美重建的应用是可接受的，特别是当被丢弃的信息对人类感官来说是不可察觉或不那么重要时。其目标是通过进行“足够好”的近似来获得显著更高的压缩比，通常是通过利用人类感知的局限性来实现。

• 核心: 永久性地丢弃部分原始数据以实现显著更高的压缩比。
• 区分: 依赖于感知限制（例如人类的视觉/听觉）来决定哪些信息可以安全移除；与无损压缩不同，原始数据无法完美重建。

3.6.1 Floating-Point Numbers (浮点数)

Floating-point numbers are a common example of an irreversible technique used to represent real numbers (which are uncountable) within a fixed number of bits in computers. This representation includes a sign, an exponent, and a mantissa (or fraction). Since only a finite number of bits are available, not all real numbers can be represented exactly. This leads to inherent precision loss and rounding errors when continuous real values are converted to discrete floating-point representations, making the conversion irreversible. While the approximation can be very good with enough bits, it is never perfect for all numbers.

• Core: A fixed-bit representation for real numbers (including fractions and very large/small numbers) using a sign, exponent, and mantissa.
• Distinction: Inherently irreversible due to finite precision, leading to rounding errors and the inability to perfectly represent all real numbers.

浮点数是计算机中一种常见的不可逆技术，用于在固定比特数内表示实数（不可数）。这种表示包括符号位、指数位和尾数（或小数）位。由于可用的比特数有限，并非所有实数都能被精确表示。这导致当连续的实数转换为离散的浮点表示时，会产生固有的精度损失和舍入误差，使得这种转换不可逆。尽管比特数足够多时近似值可以非常精确，但对于所有数字来说，它永远不会是完美的。

• 核心: 使用固定比特数（包含符号、指数和尾数）来表示实数（包括分数和极大/极小值）。
• 区分: 由于精度有限，其本质上是不可逆的，会导致舍入误差和无法完美表示所有实数。

3.6.2 JPEG Image Compression (JPEG图像压缩)

JPEG (Joint Photographic Experts Group) is a widely used irreversible compression standard for digital images, particularly photographs. It works by exploiting the human visual system's varying sensitivity to different spatial frequencies. The core steps involve:

1. Color Space Conversion: Transforming image data from RGB to YCbCr (luminance and chrominance), as human eyes are more sensitive to luminance.
2. Downsampling (Optional): Reducing the resolution of chrominance components, as color detail is less critical to perception.
3. Block Division: Dividing each component into 8x8 pixel blocks.
4. Discrete Cosine Transform (DCT): Applying DCT to each block (as discussed in Section 3.8) to convert pixel values from the spatial domain to the frequency domain. This concentrates most of the perceptually significant information into a few low-frequency coefficients.
5. Quantization: This is the lossy step. DCT coefficients are divided by values from a quantization table. Smaller values (typically high-frequency components that are less perceptible) are rounded to zero or very small integers. This permanently discards information. The quantization table can be adjusted to control the compression ratio and quality.
6. Entropy Encoding: Losslessly compressing the quantized coefficients (e.g., using Huffman coding or run-length encoding).

• Core: Irreversible image compression that leverages human visual perception limitations by discarding less important high-frequency data.
• Distinction: Utilizes DCT to transform data into frequency domain, followed by a crucial quantization step which introduces controlled information loss, allowing for flexible quality settings (higher compression means more loss).

JPEG（联合图像专家组）是一种广泛使用的数字图像（尤其是照片）不可逆压缩标准。它通过利用人类视觉系统对不同空间频率的不同敏感度来工作。核心步骤包括：

1. 色彩空间转换：将图像数据从RGB转换为YCbCr（亮度与色度），因为人眼对亮度更敏感。
2. 下采样（可选）：降低色度分量的分辨率，因为颜色细节对感知不太关键。
3. 分块：将每个分量划分为8x8像素块。
4. 离散余弦变换（DCT）：对每个块应用DCT（如3.8节所述），将像素值从空间域转换为频域。这将大部分感知上重要的信息集中到少数低频系数中。
5. 量化：这是有损步骤。DCT系数除以量化表中的值。较小的值（通常是对感知影响较小的高频分量）被四舍五入为零或非常小的整数。这会永久性地丢弃信息。量化表可以调整以控制压缩比和质量。
6. 熵编码：对量化后的系数进行无损压缩（例如，使用霍夫曼编码或行程长度编码）。

• 核心: 一种不可逆的图像压缩方法，通过丢弃不那么重要的高频数据，利用人类视觉感知的局限性。
• 区分: 利用DCT将数据转换到频域，随后通过关键的量化步骤引入可控的信息损失，从而实现灵活的质量设置（压缩比越高，损失越大）。

3.6.3 MP3 Audio Compression (MP3音频压缩)

MP3 (MPEG-1 Audio Layer 3) is a popular irreversible compression format for audio files. It achieves high compression ratios by exploiting psychoacoustic models, which describe the limitations and peculiarities of human hearing.
The main principles include:

1. Frequency Analysis: Analyzing the audio signal in the frequency domain.
2. Masking: Removing sounds that are inaudible due to auditory masking. This occurs when a louder sound makes a quieter sound at a similar frequency (or very close in time) imperceptible. MP3 algorithms identify and discard these masked sounds.
3. Irrelevant Frequencies: Discarding frequencies outside the typical human hearing range (roughly 20 Hz to 20 kHz) or those with very low amplitude that are unlikely to be heard.
4. Quantization: Applying non-uniform quantization to the remaining audio data, allocating more bits to perceptually important frequencies and fewer to less important ones.
5. Entropy Encoding: Losslessly encoding the quantized data.

• Core: Irreversible audio compression that significantly reduces file size by employing psychoacoustic models to remove inaudible or masked audio information.
• Distinction: Uniquely leverages human auditory masking and frequency perception limits to achieve high compression while aiming for minimal perceived quality loss; data once removed cannot be recovered.

MP3（MPEG-1 音频层 3）是一种流行的音频文件不可逆压缩格式。它通过利用心理声学模型（描述人类听觉的局限性和特性）来实现高压缩比。
主要原理包括：

1. 频率分析：在频域对音频信号进行分析。
2. 掩蔽效应：移除因听觉掩蔽而听不见的声音。当一个较响的声音使得频率相似（或时间上非常接近）的较安静的声音变得不可察觉时，就会发生这种情况。MP3算法识别并丢弃这些被掩蔽的声音。
3. 不相关频率：丢弃超出人类典型听力范围（大约20 Hz至20 kHz）或振幅极低、不太可能被听到的频率。
4. 量化：对剩余音频数据应用非均匀量化，将更多比特分配给感知上重要的频率，较少比特分配给不那么重要的频率。
5. 熵编码：对量化后的数据进行无损编码。

• 核心: 一种不可逆音频压缩技术，通过运用心理声学模型，移除听不见或被掩蔽的音频信息，从而显著减小文件大小。
• 区分: 独特地利用人类听觉的掩蔽效应和频率感知极限，在追求最小感知质量损失的同时实现高压缩；被移除的数据无法恢复。

3.7 Detail: LZW Compression (LZW压缩详解)

The LZW compression technique is described below and applied to two examples. Both encoders and decoders are considered. The LZW compression algorithm is “reversible,” meaning that it does not lose any information—the decoder can reconstruct the original message exactly.

下面将描述LZW压缩技术，并应用于两个示例。编码器和解码器都将进行考虑。LZW压缩算法是“可逆的”，这意味着它不会丢失任何信息——解码器可以精确地重建原始消息。

• Core: Presents the detailed algorithm for LZW compression, a reversible (lossless) technique where the decoder can exactly reconstruct the original message.

• Distinction: Emphasizes its reversibility as a key characteristic, differentiating it from irreversible techniques.

• 核心: 提供了LZW压缩的详细算法，这是一种可逆（无损）技术，解码器可以精确重建原始消息。

• 区分: 强调其可逆性是关键特征，将其与不可逆技术区分开来。

3.7.1 LZW Algorithm, Example 1 (LZW算法，示例1)

Consider the encoding and decoding of the text message
itty bitty bit bin
(this peculiar phrase was designed to have repeated strings so that the dictionary builds up rapidly).
The initial set of dictionary entries is 8-bit character code with code points 0–255, with ASCII as the first 128 characters, including the ones in Table 3.1 which appear in the string above. Dictionary entry 256 is defined as “clear dictionary” or “start,” and 257 as “end of transmission” or “stop.” The encoded message is a sequence of numbers, the codes representing dictionary entries. Initially most dictionary entries consist of a single character, but as the message is analyzed new entries are defined that stand for strings of two or more characters. The result is summarized in Table 3.2.

考虑文本消息“itty bitty bit bin”的编码和解码（这个特殊的短语被设计成包含重复字符串，以便字典快速构建）。
字典条目的初始集合是8位字符代码，代码点为0-255，其中ASCII作为前128个字符，包括表3.1中出现在上述字符串中的字符。字典条目256定义为“清除字典”或“开始”，257定义为“传输结束”或“停止”。编码消息是一系列数字，这些代码表示字典条目。最初，大多数字典条目由单个字符组成，但随着消息的分析，会定义新的条目，代表两个或更多字符的字符串。结果总结在表3.2中。

Encoding algorithm: Define a place to keep new dictionary entries while they are being constructed and call it new-entry. Start with new-entry empty, and send the start code. Then append to the new-entry the characters, one by one, from the string being compressed. As soon as new-entry fails to match any existing dictionary entry, put new-entry into the dictionary, using the next available code point, and send the code for the string without the last character (this entry is already in the dictionary). Then use the last character received as the first character of the next new-entry. When the input string ends, send the code for whatever is in new-entry followed by the stop code. That’s all there is to it.

编码算法：定义一个用于保存正在构建的新字典条目的位置，并称之为new-entry。从new-entry为空开始，并发送起始代码。然后，将要压缩的字符串中的字符逐一附加到new-entry中。一旦new-entry无法匹配任何现有字典条目，就将new-entry放入字典中，使用下一个可用的代码点，并发送不包含最后一个字符的字符串的代码（此条目已在字典中）。然后使用接收到的最后一个字符作为下一个new-entry的第一个字符。当输入字符串结束时，发送new-entry中的任何内容的代码，然后发送停止代码。就是这样。

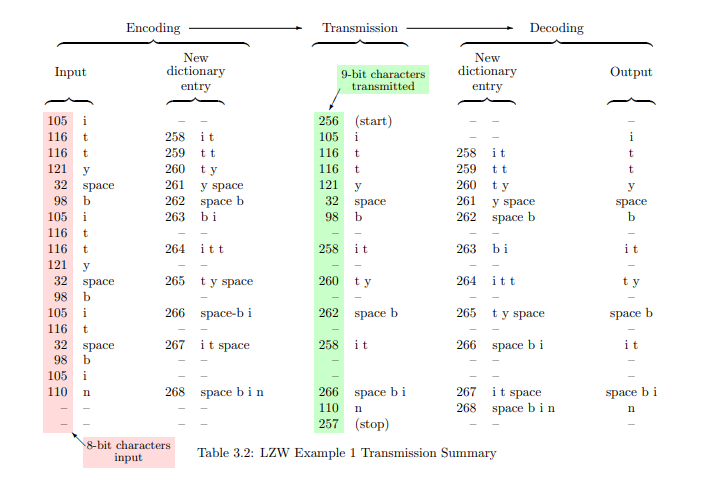
For the benefit of those who appreciate seeing algorithms written like a computer program, this encoding algorithm is shown in Figure 3.5. When this procedure is applied to the string in question, the first character is “i” and the string consisting of just that character is already in the dictionary. So the next character is appended to new-entry, and the result is “it” which is not in the dictionary. Therefore the string which was in the dictionary, “i,” is sent and the string “i t” is added to the dictionary, at the next available position, which is 258. The new-entry is reset to be just the last character, which was not sent, so it is “t”. The next character “t” is appended and the result is “tt” which is not in the dictionary. The process repeats until the end of the string is reached.
For a while at the beginning the additional dictionary entries are all two-character strings, and there is a string transmitted for every new character encountered. However, the first time one of those two-character strings is repeated, its code gets sent (using fewer bits than would be required for two characters sent separately) and a new three-character dictionary entry is defined. In this example it happens with the string “i t t” (this message was designed to make this happen earlier than would be expected with normal text). Later in this example, the code for a three-character string gets transmitted, and a four-character dictionary entry defined.
In this example the codes are sent to a receiver which is expected to decode the message and produce as output the original string. The receiver does not have access to the encoder’s dictionary and therefore the decoder must build up its own copy.

为了方便那些喜欢算法以计算机程序形式编写的人，此编码算法如图3.5所示。当此过程应用于所述字符串时，第一个字符是“i”，并且仅由该字符组成的字符串已在字典中。因此，下一个字符被附加到new-entry中，结果是“it”，这不在字典中。因此，字典中的字符串“i”被发送，并且字符串“i t”被添加到字典中，在下一个可用位置，即258。new-entry被重置为仅包含未发送的最后一个字符，因此它是“t”。下一个字符“t”被附加，结果是“tt”，这不在字典中。此过程重复直到到达字符串末尾。
开始时，额外的字典条目都是两个字符的字符串，并且每遇到一个新字符就传输一个字符串。然而，当其中一个两个字符的字符串第一次重复时，其代码就会被发送（使用的比特数少于单独发送两个字符所需的比特数），并定义一个新的三个字符的字典条目。在这个例子中，这发生在字符串“i t t”上（此消息被设计成比普通文本更早地发生这种情况）。在此示例的后期，一个三字符字符串的代码被传输，并定义了一个四字符字典条目。
在此示例中，代码被发送到接收器，接收器应解码消息并输出原始字符串。接收器无法访问编码器的字典，因此解码器必须构建自己的字典副本。

Decoding algorithm: If the start code is received, clear the dictionary and set new-entry empty. For the next received code, output the character represented by the code and also place it in new-entry. Then for subsequent codes received, append the first character of the string represented by the code to new-entry, insert the result in the dictionary, then output the string for the received code and also place it in new-entry to start the next dictionary entry. When the stop code is received, nothing needs to be done; new-entry can be abandoned.

解码算法：如果接收到起始代码，清除字典并将new-entry设为空。对于下一个接收到的代码，输出该代码所表示的字符，并将其放入new-entry中。然后对于后续接收到的代码，将该代码所表示字符串的第一个字符附加到new-entry中，将结果插入字典，然后输出接收到代码所代表的字符串，并将其放入new-entry以开始下一个字典条目。当接收到停止代码时，无需执行任何操作；new-entry可以被放弃。

This algorithm is shown in program format in Figure 3.6.
Note that the coder and decoder each create the dictionary on the fly; the dictionary therefore does not have to be explicitly transmitted, and the coder deals with the text in a single pass.
Does this work, i.e., is the number of bits needed for transmission reduced? We sent 18 8-bit characters (144 bits) in 14 9-bit transmissions (126 bits), a savings of 12.5%, for this very short example. For typical text there is not much reduction for strings under 500 bytes. Larger text files are often compressed by a factor of 2, and drawings even more.

此算法以程序格式显示在图3.6中。
请注意，编码器和解码器都会实时创建字典；因此，字典无需显式传输，并且编码器可以一次性处理文本。
这是否有效，即传输所需的比特数是否减少了？对于这个非常短的例子，我们以14次9比特传输（126比特）发送了18个8比特字符（144比特），节省了12.5%。对于典型的文本，小于500字节的字符串没有太大压缩。较大的文本文件通常可以压缩2倍，绘图甚至更多。

• Core: Illustrates the LZW encoding and decoding processes with a text example, showing how the dictionary dynamically builds up by identifying and adding frequently occurring character strings.

• Distinction: The dictionary is built "on the fly" by both encoder and decoder, eliminating the need for explicit dictionary transmission; shows effective compression even for short strings and greater savings for larger text/drawings.

• 核心: 通过文本示例说明了LZW的编码和解码过程，展示了字典如何通过识别和添加频繁出现的字符字符串而动态构建。

• 区分: 字典由编码器和解码器“实时”构建，无需显式传输字典；即使对于短字符串也能有效压缩，对于大型文本/绘图文件能实现更大节省。

3.7.2 LZW Algorithm, Example 2 (LZW算法，示例2)

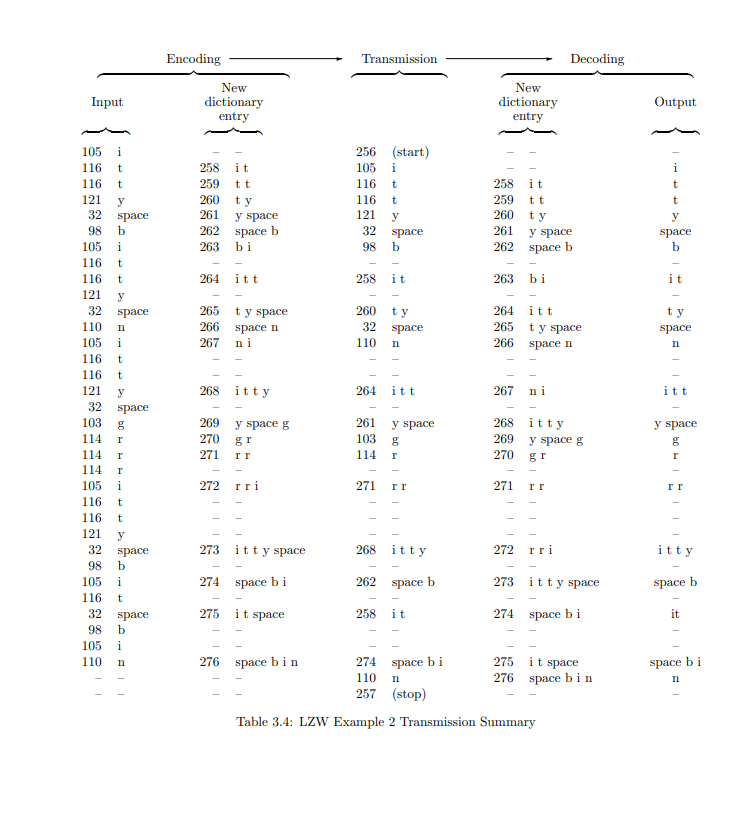
Encode and decode the text message

(again, this peculiar phrase was designed to have repeated strings so that the dictionary forms rapidly; it also has a three-long sequence rrr which illustrates one aspect of this algorithm).
The initial set of dictionary entries include the characters in Table 3.3, which are found in the string, along with control characters for start and stop.

编码和解码文本消息$$itty\ bitty\ nitty\ grrritty\ bit\ bin$$（同样，这个特殊的短语被设计成具有重复字符串，以便字典快速形成；它还包含一个由三个“r”组成的序列，这说明了该算法的一个方面）。
字典条目的初始集合包括表3.3中的字符，这些字符在该字符串中找到，以及用于开始和停止的控制字符。

The same algorithms used in Example 1 can be applied here. The result is shown in Table 3.4. Note that the dictionary builds up quite rapidly, and there is one instance of a four-character dictionary entry transmitted. Was this compression effective? Definitely. A total of 33 8-bit characters (264 bits) were sent in 22 9-bit transmissions (198 bits, even including the start and stop characters), for a saving of 25% in bits.
There is one place in this example where the decoder needs to do something unusual. Normally, on receipt of a transmitted codeword, the decoder can look up its string in the dictionary and then output it and use its first character to complete the partially formed last dictionary entry, and then start the next dictionary entry. Thus only one dictionary lookup is needed. However, the algorithm presented above uses two lookups, one for the first character, and a later one for the entire string. Why not use just one lookup for greater efficiency?
There is a special case illustrated by the transmission of code 271 in this example, where the string corresponding to the received code is not complete. The first character can be found but then before the entire string is retrieved, the entry must be completed. This happens when a character or a string appears for the first time three times in a row, and is therefore rare. The algorithm above works correctly, at a cost of an extra lookup that is seldom needed and may slow the algorithm down. A faster algorithm with a single dictionary lookup works reliably only if it detects this situation and treats it as a special case.

示例1中使用的相同算法可在此处应用。结果显示在表3.4中。请注意，字典构建速度非常快，并且有一个四字符字典条目的实例被传输。这种压缩是否有效？当然。总共33个8比特字符（264比特）通过22次9比特传输（198比特，甚至包括开始和停止字符）发送，节省了25%的比特。
在这个例子中，解码器有一个地方需要进行不寻常的操作。通常，在收到传输的码字后，解码器可以在字典中查找其字符串，然后输出它，并使用其第一个字符来完成部分形成的最后一个字典条目，然后开始下一个字典条目。这样只需要一次字典查找。然而，上面介绍的算法使用了两次查找，一次用于第一个字符，另一次用于整个字符串。为什么不只使用一次查找以提高效率呢？
此示例中代码271的传输就说明了一个特殊情况，即接收到的代码对应的字符串不完整。可以找到第一个字符，但在检索整个字符串之前，必须先完成该条目。当一个字符或字符串第一次连续出现三次时，就会发生这种情况，因此这种情况很少见。上述算法可以正确工作，但代价是额外的一次查找，这很少需要，并可能减慢算法的速度。一个使用单次字典查找的更快算法只有在检测到这种情况并将其作为特殊情况处理时才能可靠工作。

• Core: Demonstrates LZW's effectiveness for longer, repetitive strings, showing rapid dictionary growth and significant bit savings (e.g., 25% for the given example).

• Distinction: Highlights a rare "special case" in decoding (e.g., code 271) where the received string is incomplete, requiring a second dictionary lookup for correctness, which can impact efficiency if not optimized.

• 核心: 演示了LZW对更长、重复字符串的有效性，显示了字典的快速增长和显著的比特节省（例如，给定示例节省了25%）。

• 区分: 强调了解码中的一个罕见“特殊情况”（例如代码271），其中接收到的字符串不完整，需要第二次字典查找以确保正确性，如果未优化可能会影响效率。

3.8 Detail: 2-D Discrete Cosine Transformation (二维离散余弦变换详解)

This section is based on notes written by Luis P´erez-Breva, Feb 3, 2005, and notes from Joseph C. Huang, Feb 25, 2000.
The Discrete Cosine Transformation (DCT) is an integral part of the JPEG (Joint Photographic Experts Group) compression algorithm. DCT is used to convert the information in an array of picture elements (pixels) into a form in which the information that is most relevant for human perception can be identified and retained, and the information less relevant may be discarded.
DCT is one of many discrete linear transformations that might be considered for image compression. It has the advantage that fast algorithms (related to the FFT, Fast Fourier Transform) are available.
Several mathematical notations are possible to describe DCT. The most succinct is that using vectors and matrices. A vector is a one-dimensional array of numbers (or other things). It can be denoted as a single character or between large square brackets with the individual elements shown in a vertical column (a row representation, with the elements arranged horizontally, is also possible, but is usually regarded as the transpose of the vector). In these notes we will use bold-face letters (V) for vectors. A matrix is a two-dimensional array of numbers (or other things) which again may be represented by a single character or in an array between large square brackets. In these notes we will use a font called “blackboard bold” (M) for matrices. When it is necessary to indicate particular elements of a vector or matrix, a symbol with one or two subscripts is used. In the case of a vector, the single subscript is an integer in the range from 0 through n − 1 where n is the number of elements in the vector. In the case of a matrix, the first subscript denotes the row and the second the column, each an integer in the range from 0 through n − 1 where n is either the number of rows or the number of columns, which are the same only if the matrix is square.

本节基于 Luis P´erez-Breva 于2005年2月3日撰写的笔记和 Joseph C. Huang 于2000年2月25日撰写的笔记。
离散余弦变换（DCT）是JPEG（联合图像专家组）压缩算法不可或缺的一部分。DCT用于将图像元素（像素）数组中的信息转换为一种形式，使得对人类感知最相关的信息可以被识别和保留，而较不相关的信息可以被丢弃。
DCT是许多可用于图像压缩的离散线性变换之一。其优势在于有快速算法（与FFT，快速傅里叶变换相关）可用。
有多种数学符号可以描述DCT。最简洁的是使用向量和矩阵。向量是数字（或其他事物）的一维数组。它可以用单个字符表示，或用大方括号括起来，其中各个元素以垂直列显示（行表示法，元素水平排列，也是可能的，但通常被视为向量的转置）。在这些笔记中，我们将使用粗体字母（V）表示向量。矩阵是数字（或其他事物）的二维数组，同样可以用单个字符表示，或用大方括号括起来的数组表示。在这些笔记中，我们将使用名为“黑板粗体”（M）的字体表示矩阵。当需要指示向量或矩阵的特定元素时，使用带有一个或两个下标的符号。对于向量，单个下标是一个整数，范围从0到n-1，其中n是向量中元素的数量。对于矩阵，第一个下标表示行，第二个下标表示列，每个都是一个整数，范围从0到n-1，其中n是行数或列数，只有当矩阵是方阵时才相同。

• Core: Introduces Discrete Cosine Transformation (DCT) as a key component of JPEG compression, used to transform pixel data into a frequency domain representation where perceptually less relevant information can be discarded.

• Distinction: DCT is a discrete linear transformation, advantageous for its fast algorithms (related to FFT), enabling efficient image compression.

• 核心: 介绍了离散余弦变换（DCT）作为JPEG压缩算法的关键组成部分，用于将像素数据转换到频域表示，从而可以丢弃对人类感知不那么重要的信息。

• 区分: DCT是一种离散线性变换，其优势在于有快速算法（与快速傅里叶变换FFT相关），从而实现高效图像压缩。

3.8.1 Discrete Linear Transformations (离散线性变换)

In general, a discrete linear transformation takes a vector as input and returns another vector of the same size. The elements of the output vector are a linear combination of the elements of the input vector, and therefore this transformation can be carried out by matrix multiplication.
For example, consider the following matrix multiplication:
[1 1] [4] = [5]
[1 -1] [1] = [3] (3.1)
If the vectors and matrices in this equation are named
C = [1 1; 1 -1], I = [4; 1], O = [5; 3],
then Equation 3.1 becomes
O = CI. (3.2)
We can now think of C as a discrete linear transformation that transforms the input vector I into the output vector O. Incidentally, this particular transformation C is one that transforms the input vector I into a vector that contains the sum (5) and the difference (3) of its components.3
The procedure is the same for a 3×3 matrix acting on a 3 element vector:
[c1,1 c1,2 c1,3] [i1] = [o1 = Σj c1,j ij]
[c2,1 c2,2 c2,3] [i2] = [o2 = Σj c2,j ij] (3.3)
[c3,1 c3,2 c3,3] [i3] = [o3 = Σj c3,j ij]
which again can be written in the succinct form
O = CI. (3.4)

一般来说，离散线性变换以一个向量作为输入，并返回一个相同大小的另一个向量。输出向量的元素是输入向量元素的线性组合，因此这种变换可以通过矩阵乘法来实现。
例如，考虑以下矩阵乘法：
[1 1] [4] = [5]
[1 -1] [1] = [3] (3.1)
如果方程中的向量和矩阵命名为
C = [1 1; 1 -1]，I = [4; 1]，O = [5; 3]，
则方程3.1变为
O = CI。(3.2)
我们现在可以将 C 视为一个离散线性变换，它将输入向量 I 转换为输出向量 O。顺便提一下，这个特定的变换 C 是一个将输入向量 I 转换为包含其分量之和（5）和之差（3）的向量。
一个3×3矩阵作用于一个3元素向量的过程是相同的：
[c1,1 c1,2 c1,3] [i1] = [o1 = Σj c1,j ij]
[c2,1 c2,2 c2,3] [i2] = [o2 = Σj c2,j ij] (3.3)
[c3,1 c3,2 c3,3] [i3] = [o3 = Σj c3,j ij]
这再次可以用简洁的形式表示为
O = CI。(3.4)

where now the vectors are of size 3 and the matrix is 3×3.
In general, for a transformation of this form, if the matrix C has an inverse C−1 then the vector I can be reconstructed from its transform by
I = C−1O. (3.5)
Equations 3.3 and 3.1 illustrate the linear transformation when the input is a column vector. The procedure for a row-vector is similar, but the order of the vector and matrix is reversed, and the transformation matrix is transposed.4 This change is consistent with viewing a row vector as the transpose of the column vector. For example:
[4 1] [1 1; 1 -1] = [5 3]. (3.6)
Vectors are useful for dealing with objects that have a one-dimensional character, such as a sound waveform sampled a finite number of times. Images are inherently two-dimensional in nature, and it is natural to use matrices to represent the properties of the pixels of an image. Video is inherently three dimensional (two space and one time) and it is natural to use three-dimensional arrays of numbers to represent their data. The succinct vector-matrix notation given here extends gracefully to two-dimensional systems, but not to higher dimensions (other mathematical notations can be used).
Extending linear transformations to act on matrices, not just vectors, is not difficult. For example, consider a very small image of six pixels, three rows of two pixels each, or two columns of three pixels each. A number representing some property of each pixel (such as its brightness on a scale of 0 to 1) could form a 3×2 matrix:
[i1,1 i1,2]
[i2,1 i2,2]
[i3,1 i3,2] (3.7)
The most general linear transformation that leads to a 3×2 output matrix would require 36 coefficients. When the arrangement of the elements in a matrix reflects the underlying object being represented, a less general set of linear transformations, that operate on the rows and columns separately, using different matrices C and D, may be useful:
[c1,1 c1,2 c1,3] [i1,1 i1,2] [d1,1 d1,2] = [o1,1 o1,2]
[c2,1 c2,2 c2,3] [i2,1 i2,2] [d2,1 d2,2] = [o2,1 o2,2] (3.8)
[c3,1 c3,2 c3,3] [i3,1 i3,2] = [o3,1 o3,2]
或者，用矩阵表示法：
O = CID。(3.9)
请注意，在这种情况下，左侧矩阵C和右侧矩阵D通常大小不同，并且其通用特性可能相同也可能不同。（一个重要的特殊情况是当I是方阵时，即它包含相同数量的行和列。在这种情况下，输出矩阵O也是方阵，并且C和D大小相同。）

• Core: Discrete linear transformations convert an input vector to an output vector of the same size via matrix multiplication (O = CI), and can be reversed if the transformation matrix has an inverse (I = C⁻¹O). This concept extends to matrices (O = CID) for 2D data like images.

• Distinction: These transformations process rows and columns separately using different matrices for 2D objects, maintaining the spatial arrangement, unlike direct vector operations that flatten data.

• 核心: 离散线性变换通过矩阵乘法（O = CI）将输入向量转换为相同大小的输出向量，如果变换矩阵有逆矩阵（I = C⁻¹O），则该过程可逆。此概念可扩展到用于图像等二维数据的矩阵操作（O = CID）。

• 区分: 这些变换对二维对象是分别通过不同的矩阵对行和列进行操作，从而保持空间排列，这与直接将数据扁平化为向量的操作不同。

3.8.2 Discrete Cosine Transformation (离散余弦变换)

In the language of linear algebra, the formula
Y = CXD (3.10)
represents a transformation of the matrix X into a matrix of coefficients Y. Assuming that the transformation matrices C and D have inverses C−1 and D−1 respectively, the original matrix can be reconstructed from the coefficients by the reverse transformation:
X = C−1YD−1. (3.11)
This interpretation of Y as coefficients useful for the reconstruction of X is especially useful for the Discrete Cosine Transformation.
The Discrete Cosine Transformation is a Discrete Linear Transformation of the type discussed above
Y = CT XC, (3.12)
where the matrices are all of size N×N and the two transformation matrices are transposes of each other. The transformation is called the Cosine transformation because the matrix C is defined as
(2m + 1)nπ
1/N if n = 0
{C}m,n = kn cos 2N where kn = [sqrt(2/N)] otherwise (3.13)
where m, n = 0, 1, . . .(N − 1). This matrix C has an inverse which is equal to its transpose:
C−1 = CT. (3.14)
Using Equation 3.12 with C as defined in Equation 3.13, we can compute the DCT Y of any matrix X, where the matrix X may represent the pixels of a given image. In the context of the DCT, the inverse procedure outlined in equation 3.11 is called the Inverse Discrete Cosine Transformation (IDCT):
X = CYCT. (3.15)
With this equation, we can compute the set of base matrices of the DCT, that is: the set of matrices to which each of the elements of Y corresponds via the DCT. Let us construct the set of all possible images with a single non-zero pixel each. These images will represent the individual coefficients of the matrix Y.

在线性代数语言中，公式
Y = CXD (3.10)
表示将矩阵X转换为系数矩阵Y的变换。假设变换矩阵C和D分别有逆矩阵C−1和D−1，则原始矩阵可以通过逆变换从系数重建：
X = C−1YD−1。(3.11)
这种将Y解释为可用于重建X的系数的观点对于离散余弦变换特别有用。
离散余弦变换是上述讨论的一种离散线性变换
Y = CT XC，(3.12)
其中矩阵均为N×N大小，并且两个变换矩阵互为转置。该变换被称为余弦变换，因为矩阵C的定义为
(2m + 1)nπ
1/N 如果 n = 0
{C}m,n = kn cos 2N 其中 kn = [sqrt(2/N)] 否则 (3.13)
其中m, n = 0, 1, . . .(N − 1)。该矩阵C有一个逆矩阵，其等于其转置：
C−1 = CT。(3.14)
使用方程3.12和方程3.13中定义的C，我们可以计算任何矩阵X的DCT Y，其中矩阵X可以表示给定图像的像素。在DCT的上下文中，方程3.11中概述的逆过程称为逆离散余弦变换（IDCT）：
X = CYCT。(3.15)
利用这个方程，我们可以计算DCT的基矩阵集，即：Y的每个元素通过DCT对应的矩阵集。让我们构建一组所有可能的图像，每个图像只有一个非零像素。这些图像将代表矩阵Y的各个系数。

Figure 3.7(a) shows the set for 4×4 pixel images. Figure 3.7(b) shows the result of applying the IDCT to the images in Figure 3.7(a). The set of images in Figure 3.7(b) are called basis because the DCT of any of them will yield a matrix Y that has a single non-zero coefficient, and thus they represent the base images in which the DCT “decomposes” any input image.
Recalling our overview of Discrete Linear Transformations above, should we want to recover an image X from its DCT Y we would just take each element of Y and multiply it by the corresponding matrix from 3.7(b). Indeed, Figure 3.7(b) introduces a very remarkable property of the DCT basis: it encodes spatial frequency. Compression can be achieved by ignoring those spatial frequencies that have smaller DCT coefficients. Think about the image of a chessboard—it has a high spatial frequency component, and almost all of the low frequency components can be removed. Conversely, blurred images tend to have fewer higher spatial frequency components, and then high frequency components, lower right in the Figure 3.7(b), can be set to zero as an “acceptable approximation”. This is the principle for irreversible compression behind JPEG.

图3.7(a)显示了4×4像素图像的集合。图3.7(b)显示了将IDCT应用于图3.7(a)中图像的结果。图3.7(b)中的图像集合被称为基，因为其中任何一个图像的DCT都会产生一个只有一个非零系数的矩阵Y，因此它们代表了DCT“分解”任何输入图像的基图像。
回顾我们上面对离散线性变换的概述，如果我们要从其DCT Y中恢复图像X，我们只需取出Y的每个元素并将其乘以图3.7(b)中对应的矩阵。实际上，图3.7(b)引入了DCT基的一个非常显著的特性：它编码空间频率。通过忽略具有较小DCT系数的空间频率可以实现压缩。想想棋盘图像——它具有高空间频率分量，几乎所有低频分量都可以被去除。相反，模糊图像往往具有较少的高空间频率分量，此时高频分量（在图3.7(b)的右下角）可以设置为零，作为“可接受的近似”。这就是JPEG背后不可逆压缩的原理。

• Core: Discrete Cosine Transformation (DCT) is a specific type of discrete linear transformation (Y = CᵀXC) used in JPEG, where the transformation matrix C is defined using cosine functions and its inverse is its transpose (C⁻¹ = Cᵀ). This allows images (X) to be transformed into a matrix of coefficients (Y) in the spatial frequency domain.

• Distinction: The key advantage of DCT for compression is that its basis matrices (representing spatial frequencies) allow for lossy compression: coefficients corresponding to less perceptible high-frequency components (which have smaller values) can be discarded or set to zero, leading to an "acceptable approximation" (e.g., in JPEG).

• 核心: 离散余弦变换（DCT）是JPEG中使用的特定类型离散线性变换（Y = CᵀXC），其变换矩阵C由余弦函数定义，且其逆矩阵是其转置（C⁻¹ = Cᵀ）。这使得图像（X）可以被转换为空间频率域的系数矩阵（Y）。

• 区分: DCT用于压缩的关键优势在于其基矩阵（代表空间频率）允许有损压缩：对应于不那么明显的高频分量（值较小）的系数可以被丢弃或置零，从而实现“可接受的近似”（例如在JPEG中）。