1. 深度神经网络 (DNN)

1.1 神经网络 (Neural Network)

Video: https://www.bilibili.com/video/BV1bx411M7Zx/?spm_id_from=333.337.search-card.all.click&vd_source=32e3f9ea159201343145d8b8f8b9eb02

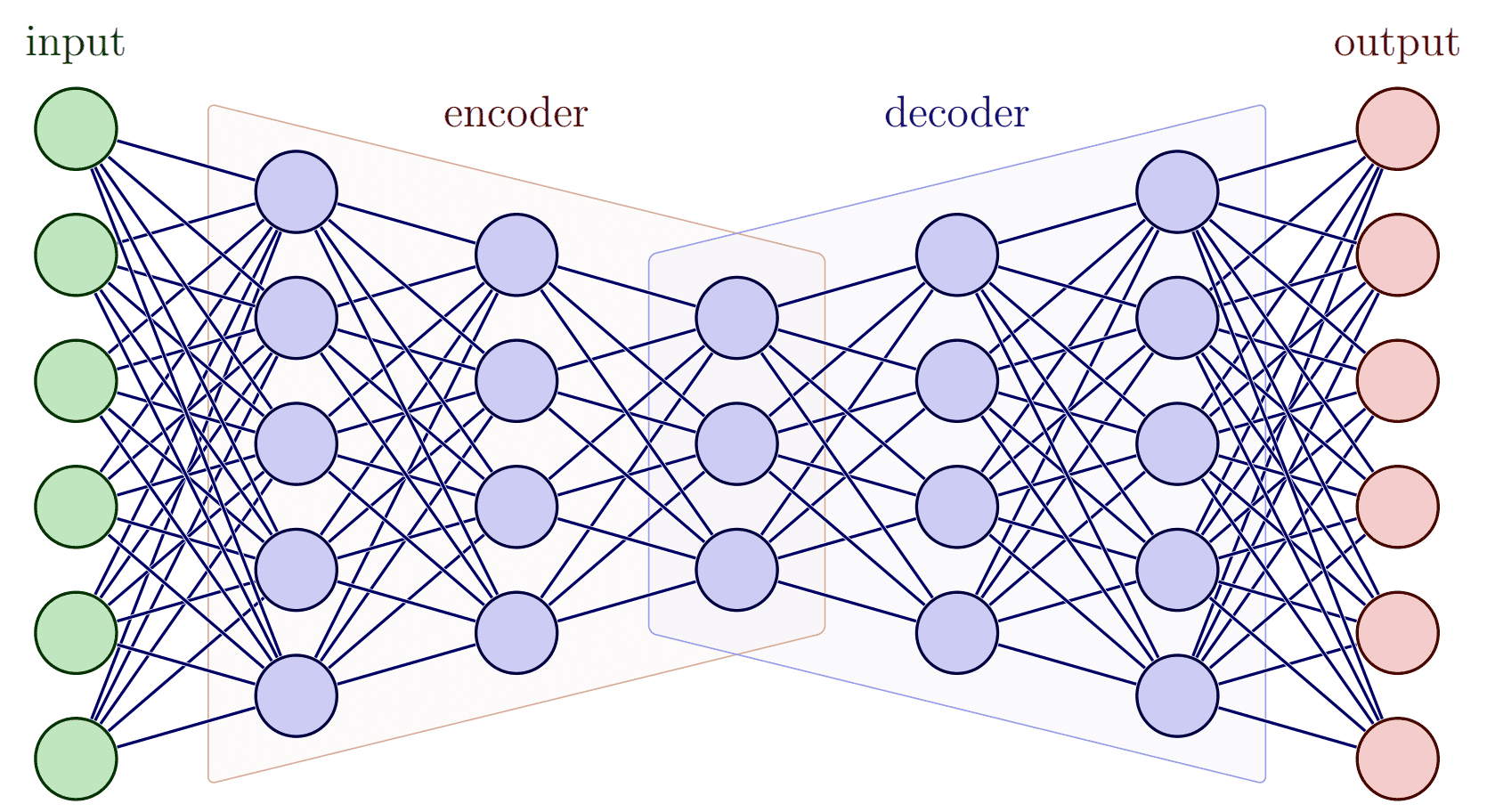
从左往右依次是：输入层 (Input Layer) 隐藏层 (Hidden Layer) 输出层 (Output Layer)

1. 输入层 (Input Layer)

   • 作用: 接收原始数据或特征。网络从这一层获取信息。

   • 神经元数量: 通常等于输入数据的特征数量。例如，如果你的输入是一张28x28像素的灰度图片，展平后输入层就有784个神经元，每个神经元对应一个像素值。

   • 计算: 输入层通常不做任何计算，它只是将输入值传递给下一层（隐藏层）。有时可能会进行一些预处理，如归一化。

1. 隐藏层 (Hidden Layer)

   • 作用: 这是网络的核心，负责从输入数据中学习和提取复杂的特征和模式。隐藏层通过对输入数据进行非线性变换，使得网络能够学习非线性关系。

   • 神经元数量: 隐藏层中神经元的数量是一个超参数，需要根据具体问题和数据进行调整和优化。可以有一个或多个隐藏层（如果多于一个隐藏层，就称为深度神经网络）。在一个“三层神经网络”的经典定义中，通常指一个隐藏层。

   • 计算:

     • 每个隐藏层的神经元都会接收来自前一层（输入层）所有神经元的加权输入。

     • 计算加权和：

     • $$z=({\omega }_1\ast x_1+{\omega }_2\ast x_2+...+{\omega }_n\ast x_n)+b$$

     • 其中 $x$ 是输入，$\omega$ 是权重，$b$ 是偏置。
       写成矩阵形式则是：

     $$\left(\begin{array}{c}{a}_0^{(j+1)}\\ a_1^{(j+1)}\\ ⋮\\ a_n^{(j+1)}\end{array}\right)=\left(\begin{array}{cccc}{\omega }_{0,0}& {\omega }_{0,1}& \cdots & {\omega }_{0,n}\\ {\omega }_{1,0}& {\omega }_{1,1}& \cdots & {\omega }_{1,n}\\ {\omega }_{2,0}& {\omega }_{2,1}& \cdots & {\omega }_{2,n}\\ ⋮& ⋮& \ddots & ⋮\\ {\omega }_{k,0}& {\omega }_{k,1}& \cdots & {\omega }_{k,n}\end{array}\right)\left(\begin{array}{c}{a}_0^{(j)}\\ a_1^{(j)}\\ ⋮\\ a_n^{(j)}\end{array}\right)+\left(\begin{array}{c}{b}_0\\ b_1\\ ⋮\\ b_n\end{array}\right)$$

     即

     $$z^{(j+1)}=W{z}^{(j)}+b$$

     训练的进行就是要改变这些参数以达到最优解

     • 将加权和通过一个激活函数 (Activation Function)（如 Sigmoid, ReLU, Tanh 等）进行非线性转换：$a=\text{activation-function}(z)$。这个激活后的值 a 会作为下一层（输出层）的输入。

     Sigmoid: ${\displaystyle \frac{1}{1+e^{-x}}}$
     ReLU: $max(0,x)$
     Tanh: $\tanh x$

- 重要性: 隐藏层的存在使得神经网络能够学习比线性模型复杂得多的函数。

1. 输出层 (Output Layer)

   • 作用: 产生网络的最终输出，即预测结果或决策。

   • 神经元数量: 输出层神经元的数量取决于具体的任务类型：

     • 二分类问题 (e.g., 是/否, 猫/狗): 通常有1个神经元，使用 Sigmoid 激活函数输出一个0到1之间的概率值。

     • 多分类问题 (e.g., 数字0-9识别): 通常有N个神经元，N等于类别数量，使用 Softmax 激活函数输出每个类别的概率分布。

     • 回归问题 (e.g., 预测房价): 通常有1个神经元（如果要预测多个值，则有对应数量的神经元），通常不使用激活函数或使用线性激活函数。

   • 计算: 与隐藏层类似，输出层的神经元接收来自前一层（隐藏层）的加权输入，计算加权和，并通过适合任务的激活函数得到最终输出。

前向传播 Forward Propagation:

数据从输入层开始，依次通过隐藏层，最后到达输出层，得到最终的预测结果。这个过程称为前向传播。

1.2 代价函数 (Cost Function / 损失函数 Loss Function)

引言 (Introduction):
在定义了神经网络的结构之后（即模型如何从输入 $x$ 得到预测输出 $\hat{y}$），我们需要一种方法来衡量模型的预测结果有多好或多差。这个衡量标准就是代价函数 (Cost Function)，有时也称为损失函数 (Loss Function) 或目标函数 (Objective Function)。代价函数量化了模型预测值与真实目标值之间的差异。我们的目标是通过调整神经网络的参数（权重 $w$ 和偏置 $b$）来最小化这个代价函数。

1. 作用 (Purpose):
   • 评估模型性能 (Evaluate Model Performance): 提供一个量化的指标来判断模型在训练数据上的表现。代价越小，通常意味着模型预测越接近真实值。
   • 指导参数优化 (Guide Parameter Optimization): 代价函数是梯度下降等优化算法的目标。优化算法通过计算代价函数关于模型参数的梯度，来朝着减小代价的方向更新参数。

2. 定义与表示 (Definition and Notation):
   • 代价函数通常表示为 $J(\theta )$ 或 $L(\theta )$，其中 $\theta$ 代表模型的所有可学习参数（例如，神经网络中的所有权重 $w$ 和偏置 $b$）。
   • 对于单个训练样本 $(x^{(i)},y^{(i)})$，我们通常先定义一个损失 (loss)，它衡量了在该样本上的预测误差，例如 $L({\hat{y}}^{(i)},y^{(i)})$。
   • 代价函数 (Cost Function) 通常是整个训练集上所有样本损失的平均值（或总和）。如果训练集有 $m$ 个样本，则：$$J(\theta )=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)}(\theta ;x^{(i)}),y^{(i)})$$其中 ${\hat{y}}^{(i)}(\theta ;x^{(i)})$ 表示模型使用参数 $\theta$ 对输入 $x^{(i)}$ 做出的预测。

3. 常见的代价函数 (Common Cost Functions):

   • 针对回归问题 (For Regression Problems):

     • 均方误差 (Mean Squared Error, MSE):
       • 公式: $J(\theta )=\frac{1}{m}\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2$
       • (有时为了求导方便会写成 $J(\theta )=\frac{1}{2m}\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2$)
       • 特点: 对误差进行平方，使得较大的误差受到更大的惩罚。是回归任务中最常用的损失函数之一。
     • 平均绝对误差 (Mean Absolute Error, MAE):
       • 公式: $J(\theta )=\frac{1}{m}\sum _{i=1}^m|{\hat{y}}^{(i)}-y^{(i)}|$
       • 特点: 对异常值不如 MSE 敏感。

   • 针对二分类问题 (For Binary Classification Problems):

     • (其中 $y^{(i)}\in \{0,1\}$，${\hat{y}}^{(i)}$ 是模型预测样本为类别 1 的概率，通常是 Sigmoid 函数的输出)
     • 二元交叉熵损失 (Binary Cross-Entropy Loss / Log Loss):
       • 单个样本的损失: $L({\hat{y}}^{(i)},y^{(i)})=-[y^{(i)}\log ({\hat{y}}^{(i)})+(1-y^{(i)})\log (1-{\hat{y}}^{(i)})]$
       • 整个数据集的代价: $J(\theta )=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log ({\hat{y}}^{(i)})+(1-y^{(i)})\log (1-{\hat{y}}^{(i)})]$
       • 特点: 当模型预测正确且置信度高时，损失小；当预测错误或置信度低时，损失大。与 Sigmoid 激活函数配合良好。

   • 针对多分类问题 (For Multi-class Classification Problems):

     • (其中类别有 $K$ 个，真实标签 $y^{(i)}$ 通常是 one-hot 编码向量，${\hat{y}}^{(i)}$ 是模型预测每个类别的概率向量，通常是 Softmax 函数的输出)
     • 分类交叉熵损失 (Categorical Cross-Entropy Loss):
       • 单个样本的损失 (假设 one-hot 编码): $L({\hat{y}}^{(i)},y^{(i)})=-\sum _{k=1}^K{y}_k^{(i)}\log ({\hat{y}}_k^{(i)})$ (其中 $y_k^{(i)}$ 是真实标签向量的第 $k$ 个元素，${\hat{y}}_k^{(i)}$ 是预测概率向量的第 $k$ 个元素)
       • 整个数据集的代价: $J(\theta )=-\frac{1}{m}\sum _{i=1}^m\sum _{k=1}^K{y}_k^{(i)}\log ({\hat{y}}_k^{(i)})$
       • 特点: 多分类问题中最常用的损失函数，与 Softmax 激活函数配合良好。

4. 选择代价函数 (Choosing a Cost Function):
   • 代价函数的选择取决于具体的任务类型（回归、二分类、多分类等）和模型的输出层激活函数。
   • 一个好的代价函数应该能够准确地反映模型的性能，并且其梯度易于计算（或具有良好的数学性质，有助于优化）。

总结 (Summary):
代价函数是连接模型预测与模型优化的桥梁。它告诉我们模型当前表现如何，并通过其梯度告诉我们应该如何调整参数以改进模型。整个训练过程的核心目标就是找到一组参数 $\theta$ 使得代价函数 $J(\theta )$ 最小化。

1.3 梯度下降 (Gradient Descent)

Video: https://www.bilibili.com/video/BV1bx411M7Zx/?spm_id_from=333.337.search-card.all.click&vd_source=32e3f9ea159201343145d8b8f8b9eb02

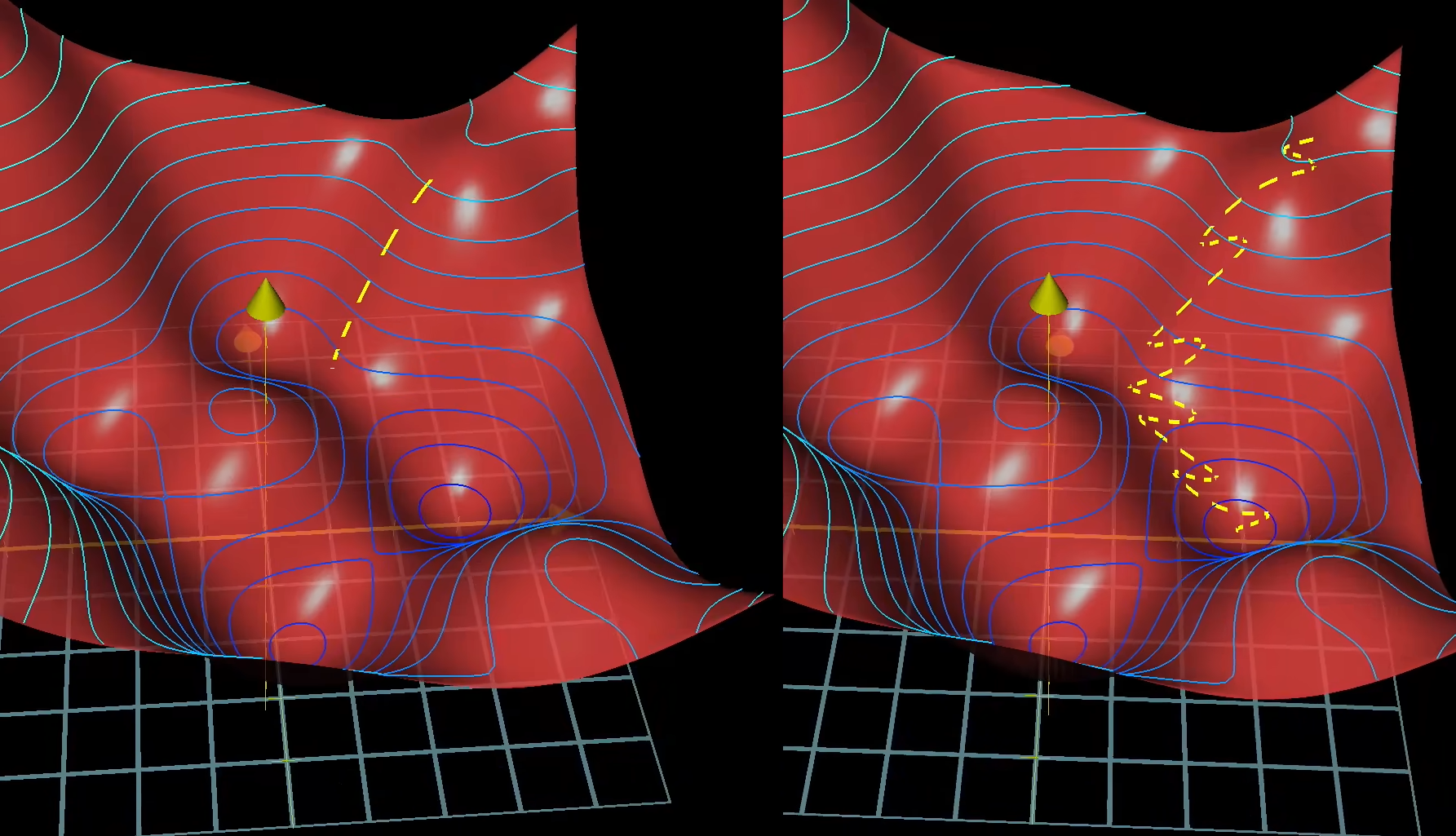
左侧：最优的梯度下降 右侧：随机梯度下降（使用Mini-batch减少了计算量）

引言 (Introduction):
在前向传播中，我们根据输入和当前的权重、偏置计算出预测结果。但是，我们如何知道当前的权重和偏置是“好”的呢？我们又该如何调整它们使得模型的预测结果更好呢？梯度下降 (Gradient Descent) 就是一种常用的优化算法，用于寻找使代价函数 (Cost Function) 最小化的模型参数（如神经网络中的权重 $\omega$ 和偏置 $b$）。它是训练神经网络的核心机制之一。

1. 目标：最小化代价函数 (Objective: Minimize Cost Function)
   • 作用: 衡量模型预测的好坏，并指导模型参数优化的方向。代价函数越小，模型预测越准确。
   • 代价函数 (Cost Function / 损失函数 Loss Function):
     • 在神经网络训练中，我们首先需要一个代价函数 (Cost Function) $J(\theta )$ (或称损失函数 Loss Function)。这里的 $\theta$ 代表模型的所有可学习参数（即权重 $\omega$ 和偏置 $b$）。
     • 代价函数用来量化模型的预测值 $(\hat{y})$ 与真实值 $(y)$ 之间的差异。
     • 常见的代价函数有：
       • 均方误差 (Mean Squared Error, MSE): 常用于回归问题。$J(\omega ,b)=\frac{1}{2m}\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2$，其中 $m$ 是样本数量。 (这里的 $\frac{1}{2}$ 是为了求导方便)
       • 交叉熵 (Cross-Entropy): 常用于分类问题。
   • 计算: 梯度下降算法的目标是迭代地调整参数 $\theta$ (即 $\omega$ 和 $b$)，以找到使代价函数 $J(\theta )$ 达到最小值的参数组合。

2. 核心思想：迭代优化 (Core Idea: Iterative Optimization)
   • 作用: 通过逐步调整参数，使代价函数的值逐渐减小，最终达到或接近最小值。
   • 直观理解 (Intuition):
     • 想象你站在一个连绵起伏的山上（代价函数的图形化表示），你的目标是走到山谷的最低点。
     • 在每一步，你都会观察当前位置哪个方向坡度最陡峭向下，然后朝着那个方向走一小步。
     • 梯度 (Gradient): 在数学上，代价函数 $J(\theta )$ 在某一点的梯度是一个向量，指向该点函数值增长最快的方向。
     • 下降 (Descent): 为了使函数值减小，我们应该沿着梯度的反方向更新参数。
   • 计算: 这是一个迭代的过程。在每一次迭代中，参数都会向着能使代价函数减小的方向进行微小的调整。

3. 关键步骤与公式 (Key Steps and Formulas)
   • 作用: 具体描述梯度下降是如何通过计算梯度来更新参数的。
   • 参数: 我们要优化的参数是神经网络中的权重 $\omega$ 和偏置 $b$。
   • 计算:
     1. 初始化参数: 随机初始化网络中的所有权重 $\omega$ 和偏置 $b$。
     2. 计算梯度 (Calculate Gradient):
        • 对于当前的参数值，计算代价函数 $J(\omega ,b)$ 关于每个参数的偏导数（梯度）。
          • $\frac{\partial J}{\partial {\omega }_{jk}^{(l)}}$ : 代价函数对第 $l$ 层，连接第 $k$ 个神经元到第 $l+1$ 层第 $j$ 个神经元的权重的偏导数。
          • $\frac{\partial J}{\partial b_j^{(l)}}$ : 代价函数对第 $l$ 层第 $j$ 个神经元的偏置的偏导数。
        • 这些偏导数指明了如果轻微增加对应参数，代价函数会增加多少。
        • 在神经网络中，这些梯度通常通过反向传播 (Backpropagation) 算法来高效计算（反向传播本身是基于链式法则的）。
     3. 更新参数 (Update Parameters):
        • 使用以下规则同时更新所有的权重和偏置：$${\omega }_{jk}^{(l)}:={\omega }_{jk}^{(l)}-\alpha \frac{\partial J}{\partial {\omega }_{jk}^{(l)}}$$$$b_j^{(l)}:=b_j^{(l)}-\alpha \frac{\partial J}{\partial b_j^{(l)}}$$
        • 其中：
          • := 表示赋值更新。
          • $\alpha$ (alpha) 是学习率 (Learning Rate)，它是一个正的小值（超参数），控制每次参数更新的“步长”。
     4. 重复: 重复步骤 2 和 3，直到代价函数 $J(\omega ,b)$ 收敛到足够小的值，或者达到预设的最大迭代次数。

4. 学习率 $\alpha$ (Learning Rate)
   • 作用: 控制参数更新的幅度或步长。选择合适的学习率对模型的训练效果和收敛速度至关重要。
   • 数值选择: 学习率是一个超参数，需要手动设置或通过实验调整。
   • 影响:
     • 学习率过小: 收敛速度会非常慢，需要大量的迭代才能达到最优解附近。
     • 学习率过大: 更新步长太大，可能会导致参数在最优解附近来回震荡，甚至可能越过最优解导致代价函数发散（不降反升），无法收敛。
     • 合适的学习率: 可以保证算法以合理的速度收敛到最优解。

5. 与神经网络训练的联系 (Connection to Neural Network Training)
   • 作用: 将梯度下降置于神经网络训练的完整流程中，解释其在优化网络参数中的核心角色。
   • 训练流程:
     1. 初始化: 随机初始化网络的权重 $\omega$ 和偏置 $b$。
     2. 迭代循环 (Epochs):
        • a. 前向传播 (Forward Propagation): 将一批训练数据输入网络，从输入层逐层计算到输出层，得到预测值 $\hat{y}$。
        • b. 计算代价 (Compute Cost): 使用代价函数 $J(\omega ,b)$ 比较预测值 $\hat{y}$ 和真实标签 $y$，计算当前参数下的代价。
        • c. 反向传播 (Backward Propagation): 从输出层开始，将代价逐层向后传播，计算代价函数 $J$ 关于网络中每一个权重 $\omega$ 和偏置 $b$ 的梯度 ($\frac{\partial J}{\partial \omega }$, $\frac{\partial J}{\partial b}$)。
        • d. 参数更新 (Update Parameters): 使用梯度下降的更新规则和学习率 $\alpha$，根据上一步计算得到的梯度来更新网络中的所有权重 $\omega$ 和偏置 $b$。
     3. 重复迭代: 不断重复整个迭代循环（通常是对整个训练数据集进行多轮迭代），直到代价函数收敛或达到预设的训练轮数。训练的进行就是要通过梯度下降不断改变这些参数($\omega ,b$)以达到最优解。

Mini-batch 梯度下降是实际训练神经网络时非常关键和常用的技术。

我们可以在梯度下降部分之后，或者作为一个更具体的梯度下降变体来介绍。这里我将其作为一个新的小节，放在梯度下降之后，反向传播之前或之后都可以，因为它本身是梯度下降的一种实现方式。

考虑到它与实际训练流程紧密相关，放在反向传播之后，作为对整个优化过程的一个更实际的补充，可能更合适。

1.3.1 Mini-batch 梯度下降 (Mini-batch Gradient Descent)

引言 (Introduction):
在前面讨论的“基础梯度下降”中，我们提到计算梯度是基于整个训练数据集的（这通常被称为批量梯度下降 Batch Gradient Descent）。当训练数据集非常庞大时，每次迭代都对所有数据计算梯度会导致计算成本极高，训练速度缓慢。另一方面，如果我们极端一些，每次只用一个样本来计算梯度并更新参数（这被称为随机梯度下降 Stochastic Gradient Descent, SGD），虽然更新快，但梯度估计的方差很大，可能导致收敛过程非常震荡。Mini-batch 梯度下降 (Mini-batch Gradient Descent) 是一种非常实用且广泛应用的折衷方案，它试图平衡计算效率和梯度估计的稳定性。

1. 目标：平衡计算效率与更新稳定性 (Objective: Balance Computational Efficiency and Update Stability)
   • 作用: 在可接受的计算时间内，实现相对稳定且快速的参数优化，特别适用于大规模数据集。
   • 核心: 每次参数更新时，不是使用全部训练数据，也不是仅使用单个训练样本，而是使用训练数据的一个小子集（这个子集称为一个 "mini-batch"）来估计梯度。
   • 优势: 它是目前训练深度神经网络最主流的优化策略之一。

2. 核心思想：分批处理与迭代 (Core Idea: Processing in Batches and Iteration)
   • 作用: 将大规模的训练任务分解为一系列在较小数据批次上的计算，从而提高训练效率并能更好地利用硬件资源。
   • Mini-batch 的定义: 整个训练数据集 $X$ 被划分为若干个不重叠（或有时允许重叠，但通常不重叠）的小数据块，每个数据块称为一个 mini-batch。例如，如果总共有 $m$ 个训练样本，每个 mini-batch 的大小 (batch size) 为 $B$，那么大约会有 $m/B$ 个 mini-batches。
   • Epoch 和 Iteration:
     • Iteration (迭代): 处理一个 mini-batch 数据并进行一次参数更新的过程称为一次迭代。
     • Epoch (轮次): 当算法处理完训练数据集中所有的 mini-batches，即对整个训练数据集完整地过了一遍之后，称为完成了一个 epoch。
   • 计算:
     • 在一个 epoch 中，算法会依次遍历所有的 mini-batches。
     • 对于每一个 mini-batch，计算该批次数据上的平均梯度（即代价函数对该批次数据的梯度）。
     • 然后使用这个 mini-batch 的梯度来更新模型的权重 $\omega$ 和偏置 $b$。

3. 关键步骤与参数 (Key Steps and Parameters)
   • 作用: 具体描述 Mini-batch 梯度下降的执行流程。
   • 参数:
     • Batch Size (批大小, $B$): 这是最重要的超参数之一，表示每个 mini-batch 中包含的训练样本数量。
       • 常见的 batch size 是 32, 64, 128, 256 等（通常是2的幂次方，以便更好地利用GPU的内存和并行计算能力）。
       • 选择影响:
         • 较小的 Batch Size: 梯度估计的噪声较大，可能导致收敛曲线震荡，但有时这种噪声有助于模型跳出局部最优点。更新更频繁。
         • 较大的 Batch Size: 梯度估计更准确，接近批量梯度下降，收敛更平稳，单次迭代计算量大，但可能更容易陷入尖锐的局部最优点。
   • 计算流程 (在一个 Epoch 内):
     1. 数据打乱 (Shuffle Data): 在每个 epoch 开始之前，通常会对整个训练数据集进行随机打乱。这样做是为了确保每个 mini-batch 的样本是随机抽取的，避免了因数据固定顺序可能带来的偏差，并增加了梯度的随机性，有助于改善训练。
     2. 划分 Mini-batches: 将打乱后的训练数据按顺序切分成多个 mini-batches，每个 mini-batch 包含 $B$ 个样本 (最后一个 mini-batch 可能不足 $B$ 个)。
     3. 遍历 Mini-batches: 对于第 $t=1,2,\dots ,(\text{num\_mini\_batches})$ 个 mini-batch：
        • a. 获取当前 Mini-batch 数据: $X^{\{t\}},Y^{\{t\}}$。
        • b. 前向传播 (Forward Propagation): 在当前 mini-batch $X^{\{t\}}$ 上进行前向传播，得到预测值 ${\hat{Y}}^{\{t\}}$。
        • c. 计算代价 (Compute Cost): 计算当前 mini-batch 上的平均代价 $J^{\{t\}}$（即该 mini-batch 中所有样本损失的平均值）。
        • d. 反向传播 (Backward Propagation): 基于当前 mini-batch 的代价 $J^{\{t\}}$，进行反向传播，计算代价函数关于模型参数 $\omega$ 和 $b$ 在这个 mini-batch 上的梯度：${\mathrm{\nabla }}_{\omega }{J}^{\{t\}}$ 和 ${\mathrm{\nabla }}_b{J}^{\{t\}}$。
        • e. 参数更新 (Update Parameters): 使用梯度下降规则更新参数：$$\omega :=\omega -\alpha {\mathrm{\nabla }}_{\omega }{J}^{\{t\}}$$$$b:=b-\alpha {\mathrm{\nabla }}_b{J}^{\{t\}}$$其中 $\alpha$ 是学习率。
     4. Epoch 结束: 当所有 mini-batches 都被处理完毕后，一个 epoch 结束。然后开始下一个 epoch（回到步骤1），重复这个过程，直到满足停止条件（如达到最大 epoch 数或代价函数收敛）。

4. 优点与权衡 (Advantages and Trade-offs)
   • 优点:
     • 计算效率: 相比于 Batch GD，每次迭代（处理一个 mini-batch）的计算量大大减少，使得训练过程更快。
     • 内存效率: 每次只需要将一个 mini-batch 的数据加载到内存中进行计算。
     • 更快的收敛: 参数更新更频繁（每个 mini-batch 更新一次，而不是每个 epoch 才更新一次），通常能比 Batch GD 更快地向最优解收敛。
     • 利用硬件并行性: 现代 GPU 等硬件非常适合并行处理大小固定的数据块 (mini-batches)。
     • 引入噪声，可能跳出局部最优: Mini-batch 梯度的随机性（因为每个 batch 的数据不同）可以看作是一种噪声，这种噪声有时能帮助算法跳出不好的局部最小值，找到更好的全局解，这类似于 SGD 的特性但更平滑。
   • 权衡:
     • Batch Size 的选择: 需要仔细调整 batch size。太小会使训练不稳定，太大则失去了 mini-batch 的一些优势（如快速迭代和噪声带来的好处），并可能增加内存需求。
     • 梯度不完全准确: Mini-batch 梯度只是对真实梯度（整个数据集上的梯度）的一个估计，因此收敛路径不会像 Batch GD 那样平滑，会有一些震荡。

5. 在神经网络训练中的核心地位 (Central Role in Neural Network Training)
   • 作用: Mini-batch 梯度下降是训练绝大多数现代深度神经网络的标准方法。
   • 与之前的流程结合:
     • 我们之前描述的神经网络训练流程中的“迭代循环”实际上指的就是对 mini-batches 的迭代。
     • 前向传播、计算代价、反向传播、参数更新这四个核心步骤都是在当前的 mini-batch 上执行的。
     • 一个 epoch 包含对所有 mini-batches 的完整遍历。
   • 进一步优化: 基于 Mini-batch 梯度下降，还发展出了许多更高级的优化算法，如 Momentum, AdaGrad, RMSProp, Adam 等，它们试图改进学习率的调整或梯度的使用方式，以获得更快的收敛速度和更好的性能，但它们的基础仍然是 Mini-batch 的处理方式。

通过使用 Mini-batch 梯度下降，我们能够在大型数据集上以可接受的计算成本和时间高效地训练复杂的神经网络模型，同时还能从梯度的适度噪声中获益。

1.4 反向传播 (Backpropagation)

Video: https://www.bilibili.com/video/BV16x411V7Qg/?spm_id_from=333.788.recommend_more_video.-1&vd_source=32e3f9ea159201343145d8b8f8b9eb02

引言 (Introduction):
在梯度下降中，我们需要计算代价函数 $J$ 对于网络中所有权重 $\omega$ 和偏置 $b$ 的偏导数（即梯度 $\frac{\partial J}{\partial \omega }$ 和 $\frac{\partial J}{\partial b}$）。对于只有少量参数的简单模型，我们可以手动推导这些梯度。但是，对于拥有成千上万甚至数百万参数的深度神经网络，手动计算变得不可行。反向传播 (Backpropagation) 是一种高效计算这些梯度的算法，它利用了微积分中的链式法则 (Chain Rule)，系统地将输出层的误差反向传播到网络中的每一层，从而计算出每个参数对总误差的贡献（即梯度）。

1. 目标：高效计算梯度 (Objective: Efficient Gradient Computation)
   • 作用: 为梯度下降算法提供必需的梯度信息，即 $\frac{\partial J}{\partial {\omega }_{jk}^{(l)}}$ 和 $\frac{\partial J}{\partial b_j^{(l)}}$。
   • 核心: 反向传播不是一个优化算法（像梯度下降那样），而是一个用于计算梯度的技术。它的核心任务是计算代价函数相对于网络中每一个可训练参数（权重和偏置）的偏导数。
   • 重要性: 没有反向传播，训练深度神经网络几乎是不可能的，因为计算梯度的复杂度会非常高。

2. 核心思想：链式法则与误差反向传播 (Core Idea: Chain Rule and Error Propagation)
   • 作用: 利用链式法则，将输出层的误差逐层向后传递，计算每一层参数对总误差的贡献。
   • 链式法则 (Chain Rule):
     • 神经网络可以看作是一个巨大的复合函数。例如，输出层的激活 $a^{(L)}$ 取决于其加权输入 $z^{(L)}$，而 $z^{(L)}$ 又取决于前一层 $a^{(L-1)}$ 的激活和权重 $W^{(L)}$，以此类推，直到输入层。
     • 如果我们想知道某个深层参数（如 $W^{(1)}$）如何影响最终的代价 $J$，我们需要通过链式法则将 $J$ 对 $a^{(L)}$ 的导数，乘以 $a^{(L)}$ 对 $z^{(L)}$ 的导数，再乘以 $z^{(L)}$ 对 $a^{(L-1)}$ 的导数，等等，一直回溯到 $W^{(1)}$。
     • 例如：若 $J=f(a)$, $a=g(z)$, $z=h(w)x+b$，则 $\frac{\partial J}{\partial w}=\frac{\partial J}{\partial a}\cdot \frac{\partial a}{\partial z}\cdot \frac{\partial z}{\partial w}$。
   • 误差反向传播 (Error Propagation):
     • 反向传播算法从输出层开始计算误差，并将这个误差“信号”向后传播到网络的每一层。
     • 对于每一层，算法会计算该层神经元的“误差项” ${\delta }^{(l)}$。这个误差项衡量了该层加权输入 $z^{(l)}$ 对最终代价函数的贡献程度。
     • 一旦计算出某层的 ${\delta }^{(l)}$，就可以很容易地计算出连接到该层的权重和偏置的梯度。

3. 关键步骤与符号 (Key Steps and Notations)
   • 作用: 描述反向传播计算梯度的具体流程。
   • 前提:
     • 已经进行了一次前向传播，计算并存储了每一层的加权输入 $z^{(l)}$ 和激活值 $a^{(l)}$。
     • $L$ 是网络的总层数。
     • $g(z)$ 是激活函数，$g^{\prime }(z)$ 是其导数。
   • 计算步骤:
     1. 计算输出层误差 (${\delta }^{(L)}$):
        • 对于输出层 $L$，计算误差项 ${\delta }^{(L)}$。这通常是代价函数对输出层加权输入 $z^{(L)}$ 的偏导数。
        • ${\delta }^{(L)}=\frac{\partial J}{\partial z^{(L)}}=\frac{\partial J}{\partial a^{(L)}}\odot g^{\prime }(z^{(L)})$
          • $\frac{\partial J}{\partial a^{(L)}}$ 是代价函数对输出层激活值的导数（例如，对于均方误差和恒等激活函数，这可能是 $(\hat{y}-y)$；对于交叉熵和Sigmoid/Softmax，形式会略有不同但可以直接计算）。
          • $g^{\prime }(z^{(L)})$ 是输出层激活函数对其输入的导数。
          • $\odot$ 表示逐元素乘积 (Hadamard product)。
     2. 反向传播误差到隐藏层 (${\delta }^{(l)}$):
        • 对于 $l=L-1,L-2,\dots ,2$ (从倒数第二层逐层向前):
        • 计算第 $l$ 层的误差项 ${\delta }^{(l)}$，它依赖于下一层（第 $l+1$ 层）的误差项 ${\delta }^{(l+1)}$ 和连接这两层的权重 $W^{(l+1)}$。
        • ${\delta }^{(l)}=((W^{(l+1)}{)}^T{\delta }^{(l+1)})\odot g^{\prime }(z^{(l)})$
          • $(W^{(l+1)}{)}^T{\delta }^{(l+1)}$ 将下一层的误差反向传播到当前层。
          • $g^{\prime }(z^{(l)})$ 是当前层激活函数对其输入的导数。
     3. 计算梯度 ($\frac{\partial J}{\partial W^{(l)}}$ 和 $\frac{\partial J}{\partial b^{(l)}}$):
        • 一旦计算出所有层的误差项 ${\delta }^{(l)}$，就可以计算代价函数 $J$ 对每一层权重 $W^{(l)}$ 和偏置 $b^{(l)}$ 的梯度：
        • $\frac{\partial J}{\partial W_{jk}^{(l)}}=a_k^{(l-1)}{\delta }_j^{(l)}$ (即代价函数对连接第 $l-1$ 层第 $k$ 个神经元到第 $l$ 层第 $j$ 个神经元的权重的梯度)
          • 写成矩阵形式：$\frac{\partial J}{\partial W^{(l)}}={\delta }^{(l)}(a^{(l-1)}{)}^T$
        • $\frac{\partial J}{\partial b_j^{(l)}}={\delta }_j^{(l)}$ (即代价函数对第 $l$ 层第 $j$ 个神经元的偏置的梯度)
          • 写成向量形式：$\frac{\partial J}{\partial b^{(l)}}={\delta }^{(l)}$
        • (注意: 如果是处理一批样本 (mini-batch)，上面的梯度通常是该批次样本梯度的平均值或总和。)

2. 卷积神经网络 (CNN)

2.1 卷积神经网络简介 (Introduction to CNN)

引言 (Introduction):
在处理图像、视频等具有空间结构的数据时，传统的深度神经网络（DNN，特指全连接网络）会遇到两个主要问题：1) 参数数量爆炸，导致模型巨大且难以训练；2) 丢失空间信息，因为它将输入的图像“压平”成一维向量。卷积神经网络 (Convolutional Neural Network, CNN) 是一种特殊类型的深度神经网络，它通过引入卷积层 (Convolutional Layer) 和池化层 (Pooling Layer) 来专门解决这些问题。CNN能够高效地从图像中提取空间层次的特征（从边缘、角点到物体的部分，再到整个物体），使其在计算机视觉领域取得了巨大成功。

2.2 CNN核心组件 (Core Components of CNN)

CNN的典型架构通常由三种主要类型的层构成：卷积层 (Convolutional Layer), 池化层 (Pooling Layer), 和全连接层 (Fully Connected Layer)。

2.2.1 卷积层 (Convolutional Layer)

作用 (Purpose):
卷积层是CNN的核心，其主要作用是通过卷积操作 (Convolution Operation) 从输入数据（通常是图像或前一层的特征图）中提取局部特征。

核心思想 (Core Ideas):

1. 局部感受野 (Local Receptive Fields):

   • 卷积层中的每个神经元只与输入的一个小区域（局部感受野）相连接，而不是像全连接层那样连接到所有输入。这符合图像处理的直觉：一个像素的含义主要由其周围的像素决定。

2. 权值共享 (Weight Sharing):

   • 一个卷积核（或称为滤波器, Filter）在整个输入图像上滑动，它使用同一组权重来检测图像不同位置的同一个特征（例如，一个用于检测垂直边缘的卷积核，在图像的左上角和右下角都使用相同的权重）。
   • 优点:
     • 大幅减少参数数量: 一个5x5的卷积核，无论输入图像多大，都只有5*5+1=26个参数（+1是偏置）。
     • 平移不变性 (Translation Invariance): 即使物体在图像中的位置发生变化，由于使用了相同的卷积核，模型仍然能够识别出该特征。

3. 权值共享 (Weight Sharing):

   • 一个卷积核（或称为滤波器, Filter）在整个输入图像上滑动，它使用同一组权重来检测图像不同位置的同一个特征（例如，一个用于检测垂直边缘的卷积核，在图像的左上角和右下角都使用相同的权重）。
   • 优点:
     • 大幅减少参数数量: 一个5x5的卷积核，无论输入图像多大，都只有5*5+1=26个参数（+1是偏置）。
     • 平移不变性 (Translation Invariance): 即使物体在图像中的位置发生变化，由于使用了相同的卷积核，模型仍然能够识别出该特征。

卷积层的优势总结 (Benefit of Convolutional Layer)

卷积层的设计哲学是基于对图像特性的深刻洞察。这张图形象地展示了卷积层是如何通过逐步放宽约束，从全连接层演变而来的，并揭示了其优势所在。

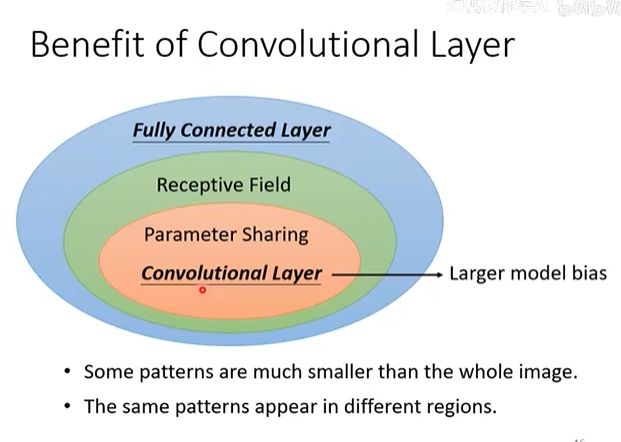
我们可以将卷积层理解为一种对全连接层施加了特定结构约束的特殊形式。从最强的约束到最弱的约束，层次关系如下：

1. 参数共享 (Parameter Sharing):

   • 这是最核心的约束。我们不为每个位置的连接都设置独立的权重，而是强制所有位置共享同一组权重（即同一个卷积核）。
   • 动机: “同样的模式可能出现在图像的不同区域 (The same patterns appear in different regions)”。例如，“鸟嘴”这个模式，无论出现在图片的左上角还是右下角，其构成模式都是相似的。因此，我们只需要一个“鸟嘴检测器”（即一个卷积核）就足够了，不需要为每个位置都训练一个独立的检测器。
   • 结果: 极大地减少了模型参数，并赋予了模型平移不变性。

2. 局部感受野 (Receptive Field):

   • 这是次一级的约束。我们假设一个神经元的输出只依赖于其输入的一个局部区域，而不是整个图像。
   • 动机: “一些模式远小于整个图像 (Some patterns are much smaller than the whole image)”。例如，识别一只猫的眼睛，我们只需要关注眼睛及其周围的一小块区域，而不需要看整张图的每一个像素。
   • 结果: 进一步减少了连接数和参数量，使得模型专注于学习有意义的局部特征。

3. 全连接层 (Fully Connected Layer):

   • 这是没有施加任何结构约束的层。每个输出神经元都连接到所有输入神经元。
   • 虽然它理论上可以学习任何函数，但由于参数量巨大且没有利用图像的空间特性，它在处理图像时效率低下且极易过拟合。

结论: 卷积层通过参数共享和局部感受野这两个强大的先验知识（或称归纳偏置, Inductive Bias），极大地优化了模型结构，使其天然地适合处理图像数据，从而获得了比全连接层更好的性能和效率。

为什么CNN的“偏见 (Bias)”反而更大？

这里的“偏见”指的是归纳偏置 (Inductive Bias)，即模型对“世界应该是什么样子”的先验假设。一个模型的归纳偏置越大，意味着它对问题的结构有越强的、越具体的假设。

我们可以将不同类型的层看作是具有不同强度归纳偏置的函数集合：

1. 全连接层 (Fully Connected Layer) - 偏置最小:

   • 它几乎没有结构性假设，只认为输入和输出之间存在某种复杂的函数关系。它不知道什么是“空间”，因此必须从海量数据中暴力地学习所有位置的关联，效率极低。

2. 引入“局部性”偏置 (Receptive Field) - 偏置增大:

   • 我们施加了第一个强假设：“一些模式远小于整个图像 (Some patterns are much smaller than the whole image)”。

   • 因此，我们设计了局部感受野，强制神经元只关注局部信息。这已经是一个强大的偏置，它告诉模型：“不要去看全局，先从局部学起！”

3. 引入“平移不变性”偏置 (Parameter Sharing) - 偏置最大:

   • 我们施加了第二个、更强的假设：“同样的模式可能出现在图像的不同区域 (The same patterns appear in different regions)”。

   • 因此，我们设计了参数共享，强制用同一个特征检测器（卷积核）去扫描整个图像。这个偏置告诉模型：“你学到的这个‘边缘检测’能力，在左上角和右下角都应该是一样的，不用重复学习！”

卷积层 (Convolutional Layer) 正是同时拥有局部感受野和参数共享这两个强大归纳偏置的层。

为什么这个强大的“偏见”是好事？
这个强大的归纳偏置，将一个几乎不可能的学习问题（像全连接层那样），转化为了一个定义良好且可解的学习问题。CNN的架构已经将“局部性”和“平移不变性”这两个宝贵的知识硬编码（hard-code）了进去。因此，它不需要从数据中浪费算力去学习这些基本规律，而是可以将宝贵的学习能力集中在更有意义的事情上：“我到底应该寻找什么样的局部模式？”（即学习卷积核的权重）。

结论: 卷积层通过引入强大的、专门针对图像的归纳偏置，极大地缩小了需要搜索的函数空间，从而用“结构上的智慧”代替了“参数上的蛮力”，获得了比全连接层更好的性能和效率。

感受野 (Receptive Field)

定义 (Definition):
在卷积神经网络中，输出特征图（Feature Map）上的一个像素点，对应到原始输入图像上的区域大小，被称为这个像素点的感受野。

换句话说，感受野告诉我们：要计算输出层某一个特定神经元的值，需要追溯到最开始的输入图像，看它依赖了多大的一块区域。

感受野的特点与重要性:

1. 逐层增大 (Increases with Depth):

   • 网络越深，感受野越大。第一层卷积层的神经元感受野很小（通常就是卷积核的大小，如3x3）。
   • 但第二层卷积层的神经元看到的是第一层的特征图，而第一层的每个像素又对应原始输入的3x3区域。因此，第二层神经元的感受野会比第一层更大。
   • 池化层 (Pooling Layer) 也会显著增大感受野。一个2x2的池化操作会让下一层的感受野近似加倍。

2. 中心点权重更高 (Center Pixels Have More Impact):

   • 虽然感受野定义了一个区域，但这个区域内的像素对输出点的影响并不是均等的。通常，靠近感受野中心的像素比边缘的像素具有更大的影响，因为它们参与计算的路径更多。

3. 感受野 vs. 卷积核大小 (Receptive Field vs. Kernel Size):

   • 卷积核大小是你在设计网络时定义的一个超参数，它决定了单次卷积操作能看到的区域大小。
   • 感受野是网络结构所带来的一个结果和属性，它描述了最终输出与原始输入之间的联系范围。

为什么感受野很重要？

• 匹配物体尺寸: 感受野的大小应该与我们想要识别的物体的尺寸相匹配。
  • 如果感受野太小，模型可能只能看到物体的局部（比如看到鸟嘴但看不到整只鸟），无法做出正确的判断。
  • 如果感受野太大，模型可能会被过多的背景信息干扰。
• 提供上下文信息: 足够大的感受野能够为模型提供必要的上下文信息，帮助它理解物体与其环境的关系。

如何增大感受野？

1. 堆叠更多的卷积层: 这是最直接的方法。
2. 使用更大的步长 (Stride) 在卷积或池化层中。
3. 使用池化层 (Pooling Layer)。
4. 使用空洞卷积 (Dilated/Atrous Convolution): 这是一种特殊的卷积，可以在不增加计算量的情况下，指数级地扩大感受野，在语义分割等任务中非常有用。

关键参数 (Key Parameters):

• 卷积核/滤波器 (Kernels / Filters):
  • 一个小型的权重矩阵（例如 3x3, 5x5）。每个卷积核负责学习并检测一种特定的局部特征（如边缘、颜色、纹理等）。
  • 一个卷积层通常包含多个卷积核，以学习多种不同的特征。
• 深度 (Depth) / 通道数 (Channels) 通道 (Channel):
  • 输出特征图的数量，等于该卷积层中使用的卷积核的数量。
• 步长 (Stride):
  • 卷积核每次滑动的像素距离。步长为1表示逐像素滑动，步长为2表示每次跳过一个像素。较大的步长会减小输出特征图的尺寸。
• 填充 (Padding):
  • 在输入图像的边界周围添加额外的像素（通常是0）。
  • 作用:
    • 保持边界信息: 如果没有填充，边界像素被卷积核扫描的次数会少于中心像素，导致信息丢失。
    • 控制输出尺寸: 使用适当的填充（如"Same" Padding）可以使输出特征图的尺寸与输入特征图保持一致。

计算 (Computation):
卷积核在输入图像上滑动，每到一个位置，就将其权重与对应的输入像素值进行逐元素相乘再求和，最后加上一个偏置项。这个结果会经过一个激活函数（通常是 ReLU），形成输出特征图中的一个像素。

2.2.2 池化层 (Pooling Layer)

作用 (Purpose):
池化层（也称为下采样层, Subsampling Layer）通常紧跟在卷积层之后，其主要作用是减小特征图的空间尺寸（宽度和高度），从而：

1. 减少计算量和参数数量，降低后续层的计算复杂度。
2. 增强模型的平移不变性，使得模型对特征的微小位置变化不那么敏感，更具鲁棒性。
3. 增大感受野，让后续的卷积层能看到更广阔的原始输入区域。

常见类型 (Common Types):

• 最大池化 (Max Pooling):
  • 计算: 在一个窗口（如2x2）内，只保留该窗口中的最大值作为输出。这是最常用的池化方法。
  • 特点: 倾向于保留最显著的特征（最强的激活信号）。
• 平均池化 (Average Pooling):
  • 计算: 计算窗口内所有值的平均值作为输出。
  • 特点: 保留了窗口内的整体背景信息。

关键参数 (Key Parameters):

• 窗口大小 (Filter/Window Size): 池化操作的区域大小，常用 2x2。
• 步长 (Stride): 池化窗口滑动的步长，通常设置为与窗口大小相同（如2），以确保窗口不重叠。

注意: 池化层没有可学习的参数（权重和偏置），它只是一个固定的下采样操作。

2.2.3 全连接层 (Fully Connected Layer)

在经过多个卷积层和池化层的特征提取后，我们得到了一组高度抽象的特征图。这些特征图是三维的张量（height x width x channels），它们很好地保留了空间信息。

然而，传统的全连接层（以及最终的Softmax分类器）需要的是一维的向量作为输入。因此，在将特征从卷积世界传递到全连接世界之前，我们需要一个关键的过渡步骤：展平 (Flatten)。

1. 展平 (Flatten)

作用 (Purpose):
Flatten 层的作用非常直接：将多维的输入（通常是最后一个卷积/池化层的三维输出）“压平”或“拉直”成一个一维的向量。它不进行任何计算，只是对数据进行一次重新排列 (reshape)。

• 假设经过最后一层池化层后，我们得到的特征图（Feature Map）的尺寸是 7 x 7 x 512 (这是一个在VGG等网络中常见的尺寸)。
• 这个三维张量包含了 7 * 7 * 512 = 25,088 个数值。
• Flatten 操作会将这个三维张量重新排列成一个包含 25,088 个元素的一维长向量。
• 这个一维向量现在可以作为第一个全连接层的输入。

在CNN架构中的位置 (Position in CNN Architecture):
Flatten 层是连接**特征提取部分（卷积和池化层）和分类/回归部分（全连接层）**的桥梁。

... -> CONV -> POOL -> **FLATTEN** -> FC -> ...

2. 全连接 (Fully Connected)

作用 (Purpose):
一旦特征被展平，全连接层就开始工作了。它的作用是综合所有高级特征（现在都在那个一维向量里了），并学习这些特征之间的非线性组合，最终完成分类或回归任务。

计算 (Computation):

• 将Flatten层输出的一维向量送入一个或多个全连接层。
• 在这些层中，每个神经元都与前一层的所有神经元相连接，进行加权求和并通过激活函数（如ReLU），最终连接到输出层。

3. 输出层 (Output Layer)

• 输出层的设计与传统的DNN完全相同，根据任务类型选择合适的神经元数量和激活函数。
  • 多分类任务: 通常使用 Softmax 激活函数，输出每个类别的概率。
  • 回归任务: 通常使用线性激活函数（即不使用激活函数），输出一个连续值。

2.3 经典CNN架构 (Classic CNN Architectures)

一个典型的CNN架构通常遵循以下模式：
INPUT -> [[CONV -> RELU] * N -> POOL?] * M -> [FC -> RELU] * K -> FC

• [CONV -> RELU]：一个卷积层后接一个ReLU激活函数。
• POOL?：一个可选的池化层。
• *N, *M, *K：表示这些模块可以重复多次。
• FC：全连接层。

示例：LeNet-5
这是最早成功应用的CNN之一，用于手写数字识别。
INPUT -> CONV1 -> POOL1 -> CONV2 -> POOL2 -> FC3 -> FC4 -> OUTPUT

示例：AlexNet
在2012年ImageNet竞赛中取得突破性成果，标志着深度学习时代的到来。它比LeNet更深更宽，并首次使用了ReLU激活函数和Dropout。

示例：VGGNet
探索了网络深度的影响，其特点是使用非常小的3x3卷积核堆叠来代替大的卷积核，结构非常规整。

示例：残差学习 (ResNet) (Residual Network)
通过引入残差块 (Residual Block) 和快捷连接 (Shortcut Connection)，成功解决了深度网络中的“网络退化”问题，使得训练数百甚至上千层的网络成为可能。这是现代CNN架构的基石。

3. 生成对抗网络 (Generative Adversarial Network, GAN)

3.1 引言：从判别式模型到生成式模型

在我们之前学习的 DNN 和 CNN 中，我们主要处理的是判别式任务 (Discriminative Tasks)。

• 判别式模型 (Discriminative Model): 学习数据之间的边界。它的目标是给定一个输入 $x$，预测出它的标签 $y$。例如，给一张图片，判断“这是猫还是狗？”。它学习的是条件概率 $P(y|x)$。

现在，我们要学习的 GAN 属于生成式模型 (Generative Model)。

• 生成式模型 (Generative Model): 学习数据的真实分布。它的目标是能够创造 (generate) 出与训练数据看起来一样但全新的数据。例如，“请画一张猫的图片”。它学习的是数据的联合概率分布 $P(x,y)$ 或边缘概率分布 $P(x)$。
  
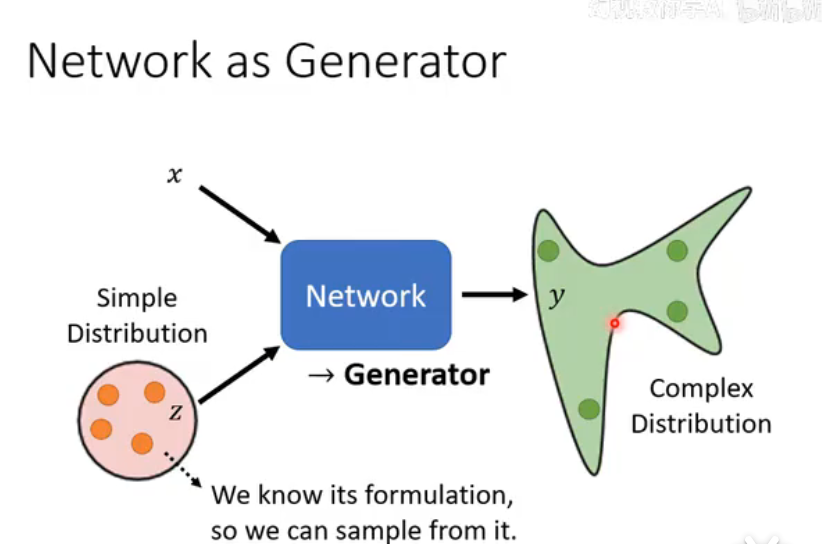
  这张图揭示了生成器 (Generator) 的本质工作：它是一个从简单分布到复杂分布的映射器 (Mapper)。

1. 左侧：简单分布 (Simple Distribution)

   • 代表: 这是一个我们完全了解并且可以轻松采样的概率分布，比如高斯分布（正态分布）。图中的文字 "We know its formulation, so we can sample from it" 指的就是这一点。
   • 作用: 我们从这个简单的分布中随机抽取一个向量 z。这个 z 就是我们用来生成图像的“随机种子”或“灵感来源”。

2. 右侧：复杂分布 (Complex Distribution)

   • 代表: 这是真实世界数据的分布，比如所有“看起来像猫”的图片的集合，或者所有“自然人脸”的集合。这个分布非常复杂，我们不知道它的数学公式。我们拥有的只是这个分布的一些样本 (samples)，也就是我们的训练数据集（比如一万张真实的猫的图片）。
   • 目标: 我们的目标就是学习这个未知的复杂分布。

3. 中间：生成器 (Generator)

   • 作用: 生成器就是一个神经网络，它学习一个复杂的函数。这个函数能够接收来自简单分布的输入 z，然后输出一个 y。
   • 训练目标: 通过训练，我们希望生成器输出的 y，能够完美地落在复杂分布的范围之内。换句话-说，我们希望生成器能将一个简单的随机数，转换成一个看起来“非常真实”的、与训练数据风格一致的全新数据。

总结: GAN的核心挑战，就是训练一个生成器网络，让它学会这个从“简单”到“复杂”的神奇映射，从而掌握真实数据的内在规律和分布。

GAN 是由 Ian Goodfellow 等人在2014年提出的，它通过一种巧妙的“对抗”机制来训练一个生成式模型。

3.2 核心思想：二人零和博弈 (A Two-Player Zero-Sum Game)

GAN 的核心思想源于博弈论。它设定了两个相互竞争的神经网络：

1. 生成器 (Generator, G): 目标是创造出以假乱真的“赝品”。

   • 类比: 一个伪钞制造者，它不断学习如何制造出越来越逼真的假钞，希望能够骗过银行。
   • 作用: 接收一个随机的噪声向量 (random noise vector, $z$)作为输入，并输出一个“假”数据（例如，一张假图片）。

2. 判别器 (Discriminator, D):

   • 角色: 判别器是GAN中的“鉴赏家”或“警察”。它的唯一目标就是尽可能准确地分辨出输入的数据是“真实的”还是由生成器“伪造的”。

   • 工作流程:

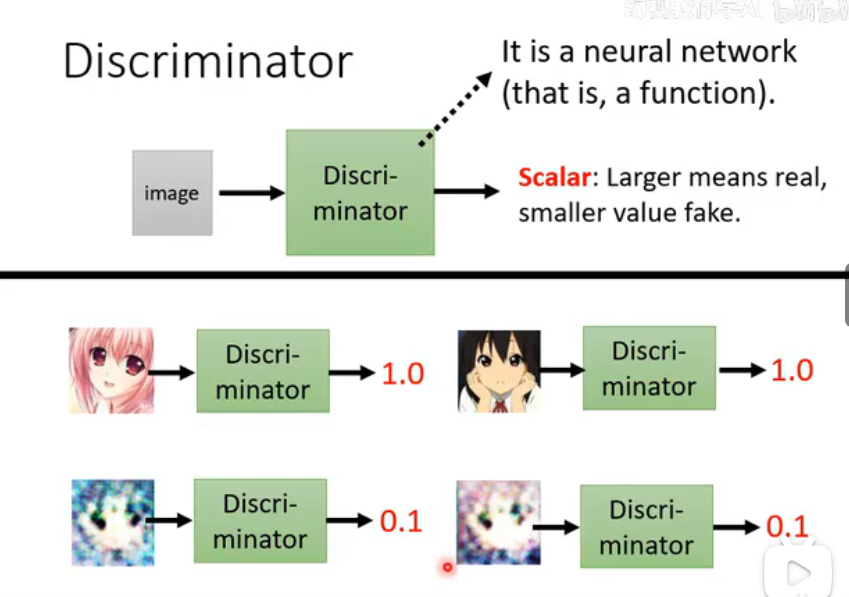
     1. 输入 (Input): 判别器接收一个数据样本，通常是一张图片。这个图片可能来自真实数据集，也可能来自生成器。判别器事先不知道图片的来源。
     2. 网络结构 (Network): 如图中所述 "It is a neural network (that is, a function)"，判别器本身就是一个神经网络。对于图像任务，它通常是一个标准的卷积神经网络 (CNN)，其设计与我们之前学习的图像分类器非常相似。
     3. 输出 (Output): 判别器最终输出一个标量 (Scalar) 值，即一个单一的数字。这个数字代表了它对输入图片“真实性”的评估。
        • 目标: "Larger means real, smaller value fake." 判别器的训练目标是：
          • 当输入真实图片时（如图中上半部分的动漫头像），它应该输出一个高分（理想情况下是 1.0）。
          • 当输入伪造图片时（如图中下半部分由早期生成器产生的模糊图像），它应该输出一个低分（理想情况下是 0 或接近 0 的值，如图中的 0.1）。
     4. 本质: 判别器本质上是在做一个二分类任务：(类别1: 真实, 类别0: 伪造)。它通过学习大量真实和伪造样本的特征，来构建一个分类边界。

   • 在整个GAN的训练框架中，一个强大的判别器是至关重要的。正是因为它能敏锐地发现生成图片的“破绽”，才能给生成器提供有价值的梯度信号，迫使生成器不断进步。

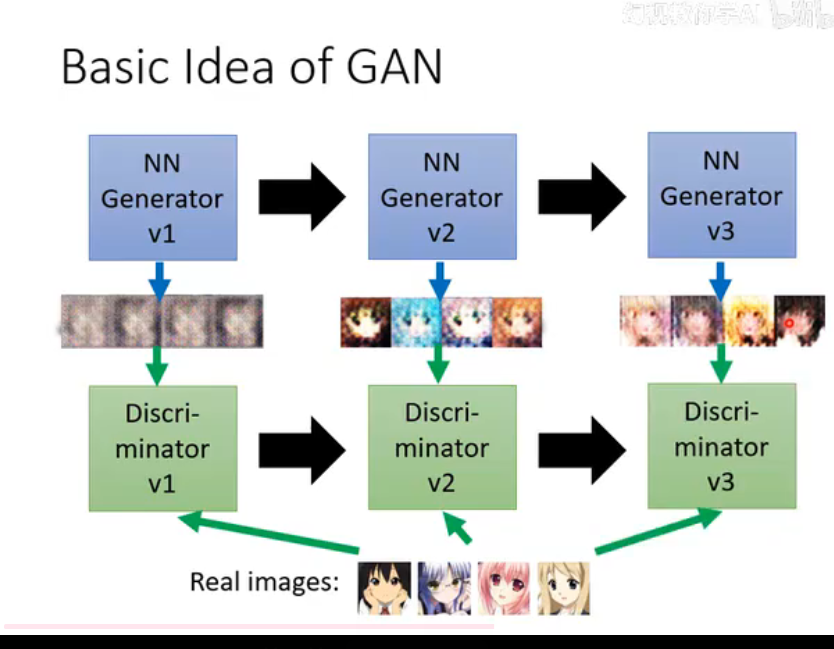
对抗训练过程 (Adversarial Training):

这两个网络被放在一起进行对抗训练，形成一个“军备竞赛”：

• 初期: 生成器 (G) 很差，只会生成随机噪声般的图片。判别器 (D) 很容易就分辨出真假。
• 训练D: 判别器 (D) 会根据自己的错误进行学习，提高自己的鉴别能力。
• 训练G: 生成器 (G) 会根据判别器 (D) 的反馈（即哪些假图片被轻易识破了）进行学习，调整自己的参数，以便生成更逼真的图片来欺骗 D。
• 循环往复: D 变得更强，迫使 G 也要变得更强。G 变得更强，又反过来促使 D 必须提升鉴别能力。
• 最终目标 (纳什均衡 Nash Equilibrium): 最终，当生成器 G 生成的图片已经逼真到让判别器 D 无法分辨（即 D 猜对的概率为 50%）时，我们就认为训练达到了一个理想状态。此时，我们得到了一个非常强大的生成器，它已经学会了真实数据的分布。

3.3 GAN 的架构与训练流程

架构 (Architecture):

1. 生成器 (Generator, G):

   • 输入: 一个随机噪声向量 $z$ (通常来自高斯分布或均匀分布)，也称为潜在向量 (Latent Vector)。
   • 网络结构: 通常使用转置卷积 (Transposed Convolution) 或称为反卷积 (Deconvolution) 的层，作用与卷积相反，可以将低维的特征图上采样 (Upsample) 到高维，最终生成一张图片。
   • 输出: 一个与真实数据维度相同的伪造数据 $G(z)$。

2. 判别器 (Discriminator, D):

   • 输入: 一张图片（真实的或伪造的）。
   • 网络结构: 通常是一个标准的卷积神经网络 (CNN) 分类器。
   • 输出: 一个介于 0 和 1 之间的标量，表示输入图片为真实的概率。 (1 代表“真实”，0 代表“伪造”)。

训练流程 (The Training "Dance"):

训练过程是交替进行的，在每次迭代中：

第一步：训练判别器 D (固定 G)

1. 固定生成器 G (Fix Generator G): 在这一步，我们冻结生成器的所有参数，不让它进行任何学习或更新。它只是一个单纯的“假货生产机器”。
2. 准备训练数据: 我们需要两类数据来喂给判别器：
   • 真实样本 (Real Objects): 从我们的真实数据库（Database）中随机抽取一批（mini-batch）图片。
   • 伪造样本 (Generated Objects): 随机生成一批噪声向量（randomly sampled vector），然后将它们输入到固定的生成器 G 中，产出一批伪造的图片。
3. 将真实图片和伪造图片都送入判别器 D。
4. 计算 D 的损失:
   • 对于真实图片 $x$，D 的预测 $D(x)$ 应该趋近于 1。
   • 对于伪造图片 $G(z)$，D 的预测 $D(G(z))$ 应该趋近于 0。
   • 损失函数通常是二元交叉熵 (Binary Cross-Entropy)。
5. 更新 D 的参数: 根据这个损失，通过反向传播只更新判别器 D 的权重。

第二步：训练生成器 G (固定 D)

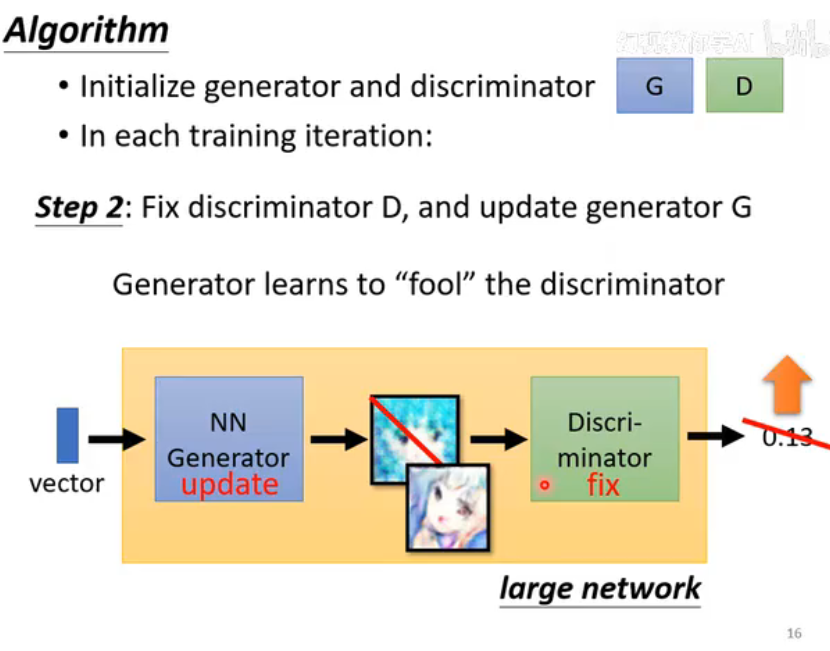
1. 生成新的一批伪造图片 $G(z)$。
2. 将这批伪造图片送入固定的判别器 D，得到预测结果 $D(G(z))$。
3. 计算 G 的损失:
   • 生成器 G 的目标是欺骗 D。它希望 D 看到自己伪造的图片 $G(z)$ 时，会输出一个接近 1 的值。
   • 因此，G 的损失是基于 $D(G(z))$ 与目标 1 之间的差距来计算的。
4. 更新 G 的参数: 根据这个损失，通过反向传播（误差会穿过固定的 D）只更新生成器 G 的权重。
   
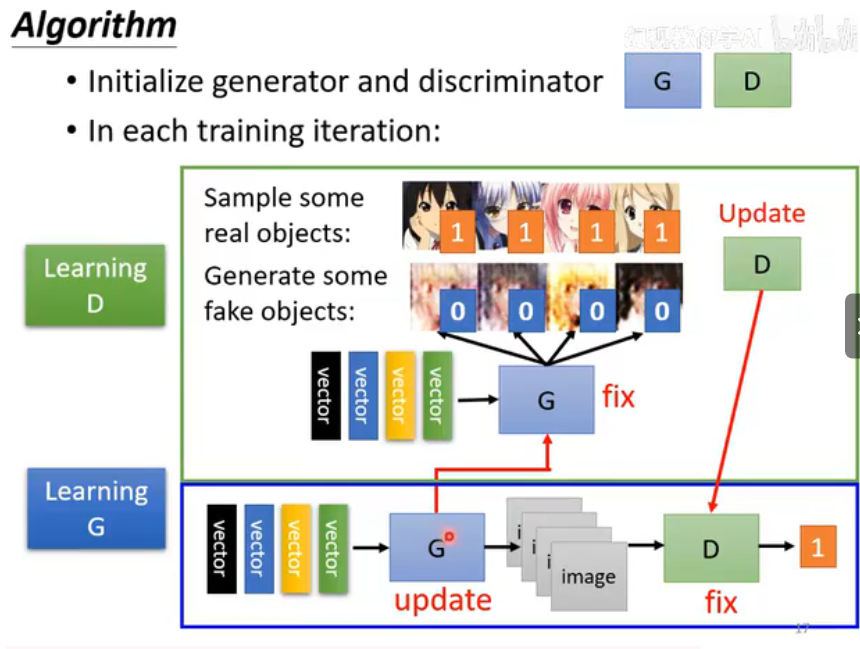
   重复以上两个步骤，直到模型收敛。

3.4 代价函数 (Cost Function)

在深入研究GAN具体的数学公式之前，我们首先要理解它的根本目标 (Our Objective)。

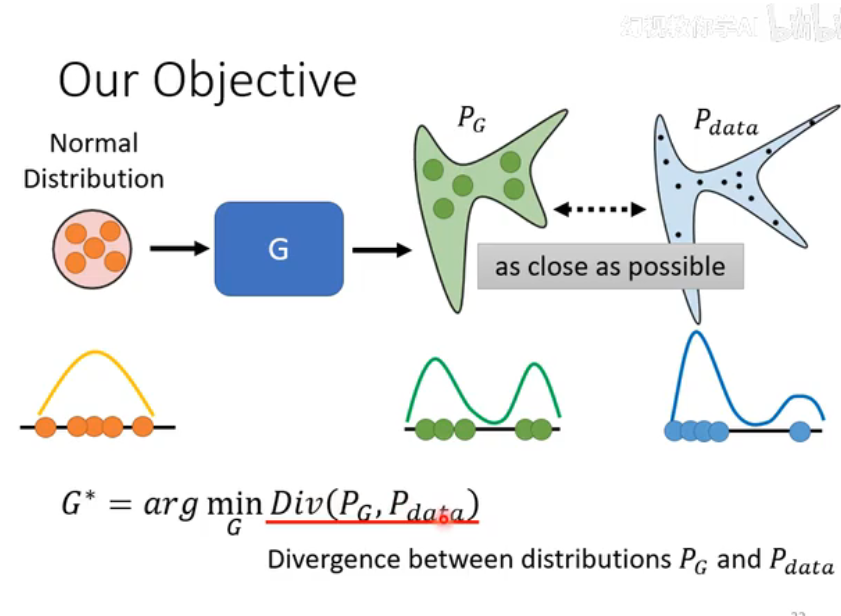
这张图告诉我们，生成器 G 的训练，本质上是一个最小化两个概率分布之间差异的过程。

1. 图中元素解读:

   • $P_{data}$ (蓝色): 真实数据（如所有真实的动漫头像）在空间中所形成的真实概率分布。这个分布是复杂且未知的，我们只有它的一些样本（我们的训练集）。
   • $P_G$ (绿色): 生成器 G 通过接收一个简单的正态分布（Normal Distribution）输入，所创造出的生成数据分布。
   • 目标 "as close as possible": 我们的终极目标，就是调整生成器 G 的参数，使得它产生的分布 $P_G$ 与真实数据的分布 $P_{data}$ 尽可能地接近。当两个分布完全重合时，就意味着生成器已经完美地学会了如何创造真实数据，以假乱真。

2. 数学目标公式:

   • 图下方的公式 G* = arg min_G Div(P_G, P_data) 是对上述目标的数学化表达。
   • $G^{\ast }$: 代表我们想要找到的最优生成器。
   • $\arg \underset{G}{min}$: 意思是“找到那个能使后面表达式最小化的G”。
   • Div(P_G, P_data): 代表一个用于衡量两个分布 $P_G$ 和 $P_{data}$ 之间差异度或散度 (Divergence) 的函数。散度越小，表示两个分布越接近。常见的散度衡量方法有KL散度(Kullback-Leibler Divergence)、JS散度(Jensen-Shannon Divergence)等。

从理论目标到GAN的巧妙实现

现在问题来了：我们并不知道 $P_{data}$ 的具体数学形式，那么如何去计算和最小化这个Div(P_G, P_data)呢？

这正是GAN最天才的地方：它不直接计算这个散度，而是设计了一个巧妙的代理任务——二人零和博弈，并利用判别器D来间接地衡量这个散度。

• 判别器D的角色: 判别器D通过不断学习来区分真实数据和生成数据，它实际上在隐式地估算 $P_G$ 和 $P_{data}$ 之间的差异。一个训练得很好的D，能敏锐地发现两个分布不重合的地方。
• GAN的代价函数: 我们接下来要学习的那个著名的最小最大博弈 (Minimax Game) 代价函数，实际上就是在优化 $P_G$ 和 $P_{data}$ 之间的 JS散度(Jensen-Shannon Divergence)。

原始 GAN 论文中提出了一个最小最大博弈 (Minimax Game) 的代价函数：

解读:

• $\underset{D}{max}$ (最大化判别器的表现): 判别器 D 想要最大化这个表达式。

  • 当输入是真实数据 $x$ 时，D 希望 $D(x)$ 趋近于 1，这样 $\log D(x)$ 趋近于 0（最大值）。
  • 当输入是伪造数据 $G(z)$ 时，D 希望 $D(G(z))$ 趋近于 0，这样 $1-D(G(z))$ 趋近于 1，$\log (1-D(G(z)))$ 趋近于 0（最大值）。
  • 所以，一个完美的 D 会让整个表达式接近 0。

• $\underset{G}{min}$ (最小化生成器的表现): 生成器 G 想要最小化这个表达式。

  • G 无法影响第一项 ${\mathbb{E}}_{x\sim p_{data}(x)}[\log D(x)]$。
  • 它只能通过调整自己来影响第二项。G 希望它生成的 $G(z)$ 能够骗过 D，即让 $D(G(z))$ 趋近于 1。
  • 当 $D(G(z))$ 趋近于 1 时，$1-D(G(z))$ 趋近于 0，$\log (1-D(G(z)))$ 会趋近于负无穷。这就实现了 G 的最小化目标。

实践中的问题与改进:
在训练初期，G 的能力很弱，D 很容易就能识别出假货（$D(G(z))\approx 0$），这会导致 $\log (1-D(G(z)))$ 的梯度非常小（梯度消失），使得 G 学习缓慢。因此在实践中，人们通常将 G 的目标函数修改为最大化 $\log (D(G(z)))$，这在早期能提供更强的梯度信号，效果更好。

3.5 挑战与重要变体

挑战 (Challenges):

• 训练不稳定 (Training Instability): G 和 D 之间的平衡非常微妙，很难协调。如果一方比另一方强太多，训练就可能崩溃。
• 模式崩溃 (Mode Collapse): 生成器 G 可能会发现一两个能稳定骗过 D 的“捷径”（例如，只生成一种类型的数字），而不再学习整个数据的分布。导致生成结果缺乏多样性。
• 评估困难: 如何客观地评价一个生成式模型的好坏本身就是一个难题。

重要变体 (Important Variants):

• DCGAN (Deep Convolutional GAN): 首次将 CNN 成功且稳定地应用到 GAN 中，提出了一系列架构设计的指导方针，是后续很多 GAN 的基础。
• cGAN (Conditional GAN): 通过给 G 和 D 同时提供一个额外的条件信息（如类别标签），可以控制 G 生成指定类别的数据。例如，命令它“生成一个数字 7”。
• WGAN (Wasserstein GAN): 采用了一种新的损失函数（Wasserstein 距离），极大地提升了训练的稳定性，并缓解了模式崩溃问题。
• CycleGAN: 实现了非配对图像到图像的转换。比如，将马的照片转换成斑马的照片，而不需要成对的“马-斑马”训练数据。
• StyleGAN: 目前生成高质量人脸等图像的最先进的模型之一，它允许对生成图像的“风格”进行精细控制。