第一讲:线性代数:线性方程组、矩阵、向量空间、线性无关
第一部分:概念
-
向量 (Vector):
可以进行加法和标量乘法(与标量相乘)运算的对象。这些运算必须满足特定的公理(例如,加法交换律,标量乘法对向量加法的分配律)。- 示例: 几何向量(二维/三维空间中的箭头)、多项式 (
)、音频信号、 中的元组(例如 )。
- 示例: 几何向量(二维/三维空间中的箭头)、多项式 (
-
封闭性 (Closure):
一个集合相对于特定运算(这里指向量加法和标量乘法)的基本性质。它意味着,如果你从集合中任意取出两个元素进行运算,其结果永远也是该集合中的一个元素。如果一个非空向量集合在向量加法和标量乘法下满足封闭性(以及其他公理),它就构成一个向量空间。- 重要性: 封闭性确保了代数结构(集合及其运算)是自洽和一致的。它是定义向量空间的基石。
-
线性方程组的解 (Solution of the linear equation system):
一个能够同时满足给定线性方程组中所有方程的 n-元组。每个分量 代表对应变量的值。 - 与向量的联系: 每个这样的 n-元组本身就是
中的一个向量。因此,求解线性方程组等价于寻找满足给定条件的特定向量。
- 与向量的联系: 每个这样的 n-元组本身就是
-
一个方程组可以有:
- 无解 (inconsistent)
- 唯一解 (unique)
- 无穷多解 (underdetermined)
-
矩阵表示法 (Matrix Notation):
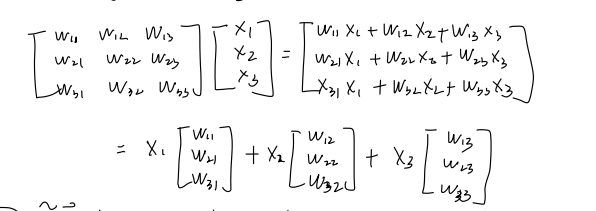
一个线性方程组可以用矩阵乘法紧凑地表示。对于一个包含个方程和 个未知数的系统: - 可以写作:
其中:是系数矩阵。 是变量向量(或未知数向量)。 是常数向量(或右侧向量)。
- 可以写作:
-
增广矩阵 (Augmented Matrix):
在使用行变换(如高斯消元法)求解线性方程组时,将系数矩阵 和常数向量 组合成一个名为增广矩阵的单一矩阵会非常方便。 - 表示法: 通常写作
[A | b],其中竖线将系数矩阵与常数向量分开。 - 结构:
如果是一个 矩阵, 是一个 的列向量,那么增广矩阵 [A | b]是一个的矩阵。
-
目的:
这种表示法允许我们对整个系统(包括系数和常数)同时执行初等行变换,从而简化求解过程。增广矩阵的每一行直接对应线性系统中的一个方程。 -
可以写作:
- 表示法: 通常写作
第二部分:矩阵运算
- 矩阵加法:
- 对于
:
- 对于
- 矩阵乘法
- 对于
:
- 仅当内部维度匹配时才定义乘法:
- 逐元素乘法称为哈达玛积 (Hadamard product):
- 单位矩阵 (Identity matrix):
- 乘法单位元:
- 代数性质:
- 结合律:
- 分配律:
- 结合律:
- 对于
- 矩阵的逆 (Matrix Inverse): 对于
,如果 ,则称 是 的逆矩阵。记作 。 - 可逆性: 如果
存在,则称 是正则的/可逆的/非奇异的。否则,它是奇异的/不可逆的。 - 唯一性: 如果
存在,则它是唯一的。 存在
- 性质:
- 可逆性: 如果
- 矩阵转置 (Matrix Transpose)
- 转置: 对于
, 定义为 。 - 性质:
- 如果
可逆,则
- 转置: 对于
- 对称矩阵 (Symmetric Matrix): 如果
,则 是对称的。 - 和: 对称矩阵的和仍然是对称的。
- 性质:
- 合同变换下的对称性:
- 实对称矩阵的可对角化性:
- 每个实对称矩阵都是可正交对角化的。这意味着存在一个正交矩阵
(其中 ) 和一个对角矩阵 ,使得 。 的对角线元素是 的特征值,而 的列是对应的标准正交特征向量。
- 每个实对称矩阵都是可正交对角化的。这意味着存在一个正交矩阵
- 标量乘法:
-
解:
- 考虑系统:
- 两个方程,四个未知数: 系统是欠定的 (underdetermined),因此我们期望有无穷多解。
- 前两列构成一个单位矩阵。这意味着
和 是主元变量(或基本变量),而 和 是自由变量。 - 为了找到一个特解,我们可以将自由变量设为零。
- 设
和 得到: - 从第一行:
- 从第二行:
- 从第一行:
- 因此,
是一个特解(也称为特殊解)。 - 为了找到非齐次系统
Ax = b的通解(描述所有无穷多解),我们需要理解相关的齐次系统Ax = 0的解。 - 考虑齐次系统:
- 同样,
和 是主元变量, 和 是自由变量。我们用自由变量来表示主元变量: - 从第一行:
- 从第二行:
- 从第一行:
- 设自由变量为参数:
和 ,其中 。 - 齐次解 (
) 可以写成向量形式:
向量
和 构成了矩阵 的零空间 (null space) 的一组基,记为 。这些有时也被称为 的特殊解。 Ax = b的通解:
一个相容的线性系统Ax = b的完整解集是任意一个特解与整个零空间 的和。
使用我们的具体例子:
这个公式描述了原始系统
Ax = b的所有无穷多解。 -
秩-零度定理 (Rank-Nullity Theorem)
-
定理陈述:
对于一个矩阵 , 的秩加上 的零度等于列数 。
即:
rank(A) + nullity(A) = n
这也意味着:
nullity(A) = n - rank(A) -
术语解释:
- A 的秩 (rank(A)):
- 定义:矩阵
的列空间 (Col(A)) 的维度。它等于 的行简化阶梯型 (RREF) 中主元变量的数量。
- 定义:矩阵
- A 的零度 (nullity(A)):
- 定义:矩阵
的零空间 (Nul(A)) 的维度。它等于 的行简化阶梯型 (RREF) 中自由变量的数量。
- 定义:矩阵
(列数 / 变量数): - 定义:矩阵
的列数,代表系统中的未知数总数。
- 定义:矩阵
- A 的秩 (rank(A)):
-
直观意义:
该定理从根本上表明,一个系统中的总变量数 () 被分为两部分:一部分受方程约束,其数量为秩;另一部分是解中可以自由选择的变量,其数量为零度。即,(主元变量数)+(自由变量数)=(总变量数)。 -
示例(使用 2x4 矩阵):
- 考虑我们之前讨论的矩阵
。 - 这里,列数
(因为有四个未知数 )。 - 该矩阵已经处于行简化阶梯型。
- 主元变量:
(对应于每行中的首个 1)。因此, rank(A) = 2。 - 自由变量:
(不对应主元位置的变量)。因此, nullity(A) = 2。
- 主元变量:
- 验证定理:
rank(A) + nullity(A) = 2 + 2 = 4。这与列数相符。 nullity(A) = n - rank(A) \implies 2 = 4 - 2。这也完全成立。
- 这个例子完美地说明了秩-零度定理。
- 考虑我们之前讨论的矩阵
-
-
初等行变换 (Elementary Row Transformations)
-
定义:
初等行变换是可以对矩阵的行执行的一组操作。这些操作至关重要,因为它们将一个矩阵转换为一个等价矩阵(意味着它们保留了相应线性系统的解集,以及矩阵的行空间、列空间维度和零空间)。 -
初等行变换的类型:
有三种基本的初等行变换:-
行交换 (Interchange Two Rows):
- 描述: 交换两行的位置。
- 表示法:
(交换第 行和第 行)
-
行缩放 (Multiply a Row by a Non-zero Scalar):
- 描述: 将一行中的所有元素乘以一个非零常数标量。
- 表示法:
(将第 行乘以标量 ,其中 )
-
行加法 (Add a Multiple of One Row to Another Row):
- 描述: 将一行的标量倍数加到另一行上。被加的行被结果替换。
- 表示法:
(将 倍的第 行加到第 行,并替换第 行)
-
-
目的和重要性:
- 求解线性系统: 初等行变换是高斯消元法和高斯-若尔当消元法的基础,这些算法通过将增广矩阵转换为行阶梯型或行简化阶梯型来求解线性方程组。
- 求矩阵的逆: 它们可用于求方阵的逆。
- 确定秩: 它们有助于找到矩阵的秩(REF, RREF 中主元/非零行的数量)。
- 寻找零空间基: 它们对于将矩阵转换为 RREF 以识别自由变量并确定零空间的基至关重要。
- 等价性: 如果一个矩阵可以通过一系列初等行变换转换为另一个矩阵,则这两个矩阵是行等价的。行等价的矩阵具有相同的行空间、零空间,因此具有相同的秩。
-
重要性:
- 如果矩阵是:
* 当且仅当
时,系统有解。
*[0 0 0 0 | 0]这一行意味着什么?
* 一行全为零,包括常数项,意味着与此行对应的原始方程是系统中其他方程的线性组合。换句话说,这个方程是多余的,没有提供关于变量的新信息。
* 关键的是,0 = 0永远是一个真命题。这表明系统是相容的(有解)。它并不意味着没有解(一个不相容的系统会有一行像[0 0 0 0 | c],其中c ≠ 0)。 -
-
行等价矩阵 (Row Equivalent Matrices)
-
定义:
如果一个矩阵可以通过有限次的初等行变换从另一个矩阵得到,则称这两个矩阵是行等价的。 -
表示法:
如果矩阵与矩阵 行等价,我们写作 , 也可写作 。 -
行等价矩阵的关键性质(保持不变的特性):
初等行变换之所以强大,是因为它们保留了矩阵的几个基本性质,这些性质对于求解线性系统和理解矩阵空间至关重要:- 线性系统具有相同的解集: 如果增广矩阵
与另一个增广矩阵 行等价,那么线性系统 与 具有完全相同的解集。 - 相同的行空间: 行空间(由矩阵行向量张成的向量空间)在初等行变换下保持不变。
- 相同的零空间: 零空间(齐次方程
的所有解的集合)保持不变。 - 相同的秩: 由于行空间和零空间的维度被保留,矩阵的秩(等于列空间的维度,也等于行空间的维度)也被保留。
- 相同的行简化阶梯型 (RREF): 每个矩阵都行等价于一个唯一的行简化阶梯型 (RREF)。
- 线性系统具有相同的解集: 如果增广矩阵
-
-
通过增广矩阵计算逆矩阵:
行简化阶梯型 (RREF) 对于求矩阵的逆非常有用。这种策略也被称为高斯-若尔当消元法求逆。- 要求: 矩阵 A 必须是方阵 (
)。 - 核心思想: 计算
实质上是求解矩阵方程 。 - 步骤:
- 写出增广矩阵
[A | I_n]: - 执行高斯消元法(行化简): 使用初等行变换将左侧的
变为单位矩阵 。 - 读取逆矩阵: 如果左侧成功变为
,那么右侧的矩阵就是 。 - 不可逆的情况: 如果在行化简过程中,左侧无法变为
(例如,出现一个全零行),则矩阵 是奇异的(不可逆), 不存在。 - 证明: Compatibility of Matrix Multiplication with Partitioned Matrices
- 写出增广矩阵
- 限制: 对于非方阵,此方法不适用。
- 要求: 矩阵 A 必须是方阵 (
-
求解线性系统 (
Ax = b) 的算法:直接法-
1. 直接求逆法:
- 适用性: 当系数矩阵
是方阵且可逆时。 - 公式:
- 适用性: 当系数矩阵
-
2. 伪逆法 (Moore Penrose Pseudo inverse):
- 适用性: 当
不是方阵但列线性无关(即满列秩)时。这在超定系统(方程多于未知数, )中很常见。 - 公式:
- 结果: 这个公式给出了最小范数最小二乘解。它找到使残差的欧几里得范数
最小化的向量 。
- 适用性: 当
-
局限性 (求逆法和伪逆法的共同点):
- 计算成本高: 计算矩阵的逆或伪逆通常计算成本很高,对于一个
矩阵,其计算成本通常为 。 - 数值不稳定: 对于大型或病态系统,这些方法可能数值不稳定。
- 计算成本高: 计算矩阵的逆或伪逆通常计算成本很高,对于一个
-
3. 高斯消元法:
- 机制: 一种系统性的方法,通过一系列初等行变换将增广矩阵
[A | b]简化为行阶梯型或行简化阶梯型来求解Ax = b。 - 可扩展性: 高斯消元法对于数千个变量通常是高效的。但对于非常大的系统(例如数百万个变量)则不实用,因为其计算成本随变量数量呈立方级增长 (
)。
- 机制: 一种系统性的方法,通过一系列初等行变换将增广矩阵
-
第三部分:向量空间与群
-
群 (Group):
一个群是一个集合与一个二元运算 的组合,该运算满足以下四个公理: - 封闭性: 对所有
, 的结果也在 中。 - 结合律: 对所有
, 。 - 单位元: 存在一个元素
(称为单位元),使得对每个 , 。 - 逆元: 对每个
,存在一个元素 (称为 的逆元),使得 。
附加术语:
- 阿贝尔群 (Abelian Group)(交换群): 如果运算
还满足交换律(即对所有 , ),则该群称为阿贝尔群。



- 封闭性: 对所有
笔记续
-
向量空间 (Vector Space):
一个向量空间是一个由称为向量的对象组成的集合 (),以及一个标量集合(通常是实数 ),配备了向量加法和标量乘法两种运算。这些运算必须满足十个公理。 向量空间的公理:
设是 中的向量, 是 中的标量。 -
加法封闭性:
在 中。 -
加法交换律:
。 -
加法结合律:
。 -
零向量(加法单位元):
中存在一个向量 ,使得 。 -
加法逆元: 对每个向量
, 中存在一个向量 ,使得 。 - 与群的联系: 前五个公理意味着向量集合
与加法运算 构成一个阿贝尔群。
- 与群的联系: 前五个公理意味着向量集合
-
标量乘法封闭性:
在 中。 -
分配律:
。 -
分配律:
。 -
标量乘法结合律:
。 -
标量单位元:
。
-
-
子空间 (Subspace):
向量空间的一个子空间是 的一个子集 ,它本身在 上定义的相同加法和标量乘法运算下也是一个向量空间。 - 子空间判别法: 要验证一个子集
是否为子空间,只需检查三个条件: - 包含零向量:
的零向量在 中( )。 - 加法封闭性: 对任意两个向量
,它们的和 也在 中。 - 标量乘法封闭性: 对任意向量
和任意标量 ,向量 也在 中。
- 包含零向量:
- 关键示例:
中任何穿过原点的直线或平面都是 的子空间。 矩阵 的零空间,记为 ,是 的一个子空间。 矩阵 的列空间,记为 ,是 的一个子空间。
- 子空间判别法: 要验证一个子集
-
线性组合 (Linear Combination):
给定向量空间中的向量 和标量 ,由下式定义的向量 : 被称为
的一个线性组合,其权重为 。 -
生成空间 (Span):
- 定义: 一组向量
的生成空间,记为 ,是这些向量所有可能的线性组合的集合。 - 几何解释:
(其中 )是穿过原点和 的直线。 (其中 不共线)是包含原点、 和 的平面。
- 性质: 任何向量集的生成空间永远是一个子空间。
- 定义: 一组向量
-
线性无关与线性相关 (Linear Independence and Dependence):
- 线性无关: 如果向量方程
只有平凡解( ),则向量集 是线性无关的。 - 线性相关: 如果存在不全为零的权重
使得该方程成立,则该集合是线性相关的。 - 直观意义: 一组向量是线性相关的,当且仅当至少有一个向量可以写成其他向量的线性组合。线性无关的向量是无冗余的。
- 线性无关: 如果向量方程
-
基 (Basis):
向量空间的一个基是一个向量集合 ,它满足两个条件: - 集合
是线性无关的。 - 集合
生成整个向量空间 (即 )。
- 基是构建整个空间所需的“最小”向量集合。
- 集合
-
维度 (Dimension):
- 定义: 非零向量空间
的维度,记为 ,是 的任意一个基中的向量数量。零向量空间 的维度定义为 0。 - 唯一性: 虽然一个向量空间可以有许多不同的基,但给定向量空间的所有基都具有相同数量的向量。
- 与秩-零度定理的联系:
- 矩阵
的列空间的维度是其秩: 。 - 矩阵
的零空间的维度是其零度: 。
- 矩阵
- 定义: 非零向量空间
-
使用高斯消元法检验线性无关性:
要检验一组向量是否线性无关: - 将这些向量作为列,构成一个矩阵
。 - 对矩阵
执行高斯消元,将其化为行阶梯型。
- 与主元列对应的原始向量是线性无关的。
- 与非主元列对应的向量可以写成前面主元列的线性组合。
示例: 在以下行阶梯型矩阵中:
第 1 列和第 3 列是主元列(它们对应的原始向量是无关的);第 2 列是非主元列(它对应的原始向量是相关的)。
因此,原始向量集(矩阵
的列)不是线性无关的,因为至少有一个非主元列。换句话说,该集合是线性相关的。 - 将这些向量作为列,构成一个矩阵
-
线性组合的线性无关性
假设我们有一组个线性无关的向量 ,可以看作是 维空间的一个基。我们可以构造一组新的 个向量 ,其中每个 都是基向量的线性组合: 每组权重可以表示为一个系数向量
。 - 关键推论: 新向量集
是线性无关的,当且仅当 它们对应的系数向量集 是线性无关的。
- 关键推论: 新向量集
-
生成集的维度定理 (一个基本定理)
向量空间的维度不能超过其任何生成集中的向量数量。一个直接的推论是,在维度为的向量空间中,任何包含超过 个向量的集合必定是线性相关的。 -
特殊情况:新向量数量多于基向量数量 (
) 定理: 如果你用
个线性无关的向量来生成 个新向量,并且 ,那么得到的新向量集 永远是线性相关的。 证明 (使用矩阵的秩):
-
关注系数向量: 如上所述,
的线性无关性等价于其系数向量 的线性无关性。我们将证明集合 必定是线性相关的。 -
构造系数矩阵: 让我们将这些系数向量排列成一个矩阵
的列: 由于每个系数向量
都在 中,矩阵 有 行和 列(它是一个 矩阵)。 -
分析矩阵的秩: 矩阵的秩有一个基本性质:它不能超过其行数或列数。具体来说,我们关心的是
(行数)。 - (通过一个更基本的定理证明:秩是行空间的维度。行空间由
个行向量生成。根据The Dimension Theorem for Spanning Sets,这个空间的维度不能超过 )。
- (通过一个更基本的定理证明:秩是行空间的维度。行空间由
-
应用条件
: 我们已经确定了关于矩阵 的两个关键事实: - 总列数为
。 - 秩,代表线性无关列的最大数量,最多为
。即 。
- 总列数为
-
将秩与线性相关性联系起来: 我们已知
。这导致了一个关键的不等式: 这个不等式意味着
的所有 个列不可能都是线性无关的。如果你拥有的向量数量( )超过了它们可以生成的空间的维度(秩,最多为 ),那么这个向量集必定是线性相关的。 -
得出结论: 因为
的列(即系数向量 )构成一个线性相关的集合,所以由它们定义的新向量集 也必定是线性相关的。证毕。
-
第二讲:线性代数:基与秩、线性映射、仿射空间
第一部分:基与秩
-
生成集 (Generating Set or Spanning Set)
- 定义: 如果
,则向量集 被称为向量空间 的一个生成集。 - 关键思想: 生成集可能是冗余的;它可能包含线性相关的向量。
- 示例: 集合
是 的一个生成集。它是冗余的,因为 是另外两个向量的线性组合。
- 定义: 如果
-
生成空间 (Span) 的附加属性
- 与线性系统的联系: 线性方程组
有解,当且仅当向量 位于矩阵 的列的生成空间中。即 。
- 与线性系统的联系: 线性方程组
-
基 (Basis) 的附加属性
- 唯一表示定理: 基的一个关键性质是,空间中的每个向量
都可以用唯一的方式表示为基向量的线性组合。这个唯一组合的系数被称为 相对于该基的坐标。 - 示例(标准基):
最常用的基是标准基,它由 单位矩阵 的列组成。对于 ,标准基是 。
- 唯一表示定理: 基的一个关键性质是,空间中的每个向量
-
基的特征
对于向量空间中的一个非空向量集 ,以下陈述是等价的(即如果一个为真,则全部为真): 是 的一个基。 是一个最小生成集(即它生成 ,但 的任何真子集都不能生成 )。 是一个最大线性无关集(即它是线性无关的,但向其中添加任何其他来自 的向量都会使该集线性相关)。
-
维度的进一步性质
- 存在性与规模的唯一性: 每个非平凡的向量空间都有一个基。虽然一个空间可以有许多不同的基,但它们都将具有相同数量的向量。这使得维度的概念是明确定义的。
- 子空间维度: 如果
是向量空间 的一个子空间,那么 。等号成立当且仅当 。 - 重要澄清: 空间的维度指的是其基中向量的数量,而不是每个向量中的分量数量。例如,由单个向量
生成的子空间是一维的,尽管该向量存在于 中。
-
如何为子空间找到一个基(基提取法)
为由一组向量
的生成空间定义的子空间 找到一个基: - 创建一个矩阵
,其列为向量 。 - 将矩阵
化简为其行阶梯型。 - 识别包含主元的列。
的基由集合 中与这些主元列对应的原始向量组成。
- 创建一个矩阵
-
矩阵的秩
- 定义: 矩阵
的秩,记为 ,是 中线性无关列的数量。线性代数的一个基本定理指出,这个数字总是等于线性无关行的数量。 - 关键性质: 矩阵的秩等于其转置的秩:
。
- 定义: 矩阵
-
秩及其与基本子空间的联系
- 列空间 (像/值域):
的秩是其列空间的维度。
- 零空间 (核): 秩通过秩-零度定理确定了零空间的维度。对于一个
矩阵 :
- 列空间 (像/值域):
-
秩的性质和应用
- 方阵的可逆性: 一个
矩阵 是可逆的,当且仅当其秩等于其维度,即 。 - 线性系统的可解性: 系统
至少有一个解,当且仅当系数矩阵 的秩等于增广矩阵 的秩。 - 满秩和秩亏:
- 如果一个矩阵的秩是其维度可能的最大值,则该矩阵为满秩:
。 - 如果
,则矩阵是秩亏的,表明其行或列之间存在线性相关性。
- 如果一个矩阵的秩是其维度可能的最大值,则该矩阵为满秩:
- 方阵的可逆性: 一个
-
为什么秩很重要
矩阵的秩是揭示其基本结构的核心概念。它告诉我们:
- 线性无关行/列的最大数量。
- 数据的维度(由列生成的子空间的维度)。
- 线性系统是否相容(有解)。
- 方阵是否有逆。
- 它对于识别冗余和简化数据分析、优化和机器学习中的问题至关重要。
-
总结:将秩、基和主元联系起来
- 你从一组向量开始。
- 你将它们作为列放入矩阵
中。 - 你执行高斯消元法找到主元。
- 主元的数量就是矩阵
的秩。 - 这个秩也是由原始向量生成的子空间的维度。
- 与主元列对应的原始向量构成了该子空间的一个基。
第二部分:线性映射
-
线性映射 (Linear Mappings / Linear Transformations)
- 定义: 从向量空间
到向量空间 的一个映射(或函数) 被称为线性的,如果它保持了两个基本的向量空间运算: - 可加性: 对所有
, 。 - 齐次性: 对任何标量
, 。
- 可加性: 对所有
- 矩阵表示: 任何有限维向量空间之间的线性映射都可以通过矩阵乘法来表示:
,其中 是某个矩阵。
- 定义: 从向量空间
-
映射的性质:单射、满射、双射
- 单射 (Injective / One-to-one): 如果不同的输入总是映射到不同的输出,则映射是单射的。
- 满射 (Surjective / Onto): 如果映射的值域等于其陪域,则映射是满射的。这意味着目标空间
中的每个元素都是起始空间 中至少一个元素的像。 - 双射 (Bijective): 如果一个映射既是单射又是满射,则它是双射的。双射映射有一个唯一的逆映射
。
-
特殊类型的线性映射
- 同态 (Homomorphism): 对于向量空间,同态只是线性映射的另一个术语。
- 同构 (Isomorphism): 既是线性映射又是双射的映射。同构的向量空间在结构上是相同的。
- 自同态 (Endomorphism): 从一个向量空间到其自身的线性映射(
)。 - 自同构 (Automorphism): 既是自同态又是双射的映射。它是从一个向量空间到其自身的同构(例如,旋转或反射)。
- 恒等映射 (Identity Mapping): 由
定义的映射。
-
同构 (Isomorphism)
- 同构与维度: 一个基本定理指出,两个有限维向量空间
和 是同构的(结构上相同),当且仅当它们具有相同的维度。
- 直观理解: 这意味着任何n维向量空间本质上都是
的一个“重新标记”。
- 同构与维度: 一个基本定理指出,两个有限维向量空间
-
通过有序基的矩阵表示
通过选择一个有序基,抽象的n维空间和具体的空间 之间的同构关系变得实用。基向量的顺序对于定义坐标很重要。 - 表示法: 我们用括号表示一个有序基,例如
。
- 表示法: 我们用括号表示一个有序基,例如
-
坐标和坐标向量
- 定义: 给定
的一个有序基 ,每个向量 都可以唯一地写成: 标量 被称为 相对于基 的坐标。 - 坐标向量: 我们将这些坐标收集成一个列向量,它在标准空间
中表示 :
- 定义: 给定
-
坐标系和基变换
- 概念: 一个基为向量空间定义了一个坐标系。
中熟悉的笛卡尔坐标只是相对于标准基 的坐标。任何其他基都定义了一个不同但同样有效的坐标系。
- 概念: 一个基为向量空间定义了一个坐标系。
-
对线性映射的重要性
一旦我们为输入和输出空间固定了有序基,我们就可以将任何线性映射表示为一个具体的矩阵。这个矩阵表示完全依赖于所选的基。
第三部分:基变换和变换矩阵
本节涵盖了将抽象线性映射表示为矩阵以及改变坐标系的机制。
1. 线性映射的变换矩阵
变换矩阵为抽象的线性映射提供了一个具体的计算表示,这是相对于所选基而言的。
-
定义和背景:
我们给定一个线性映射,向量空间 的一个有序基 ,以及向量空间 的一个有序基 。 -
变换矩阵 (
) 的构造:
变换矩阵是一个 矩阵,其列描述了输入基向量如何被 变换。构造如下: - 对每个输入基向量
(从 到 ): - 应用线性映射得到其像:
。 - 将这个像表示为输出基向量
的唯一线性组合: - 这个组合的系数构成了矩阵
的第 列。这一列是 相对于基 的坐标向量:
- 对每个输入基向量
-
用法和解释:
这个矩阵将任何的坐标向量(相对于基 )映射到其像 的坐标向量(相对于基 )。核心运算公式是: 这个公式将抽象的函数应用转化为具体的矩阵-向量乘法。矩阵
是映射 相对于所选基的表示;改变任何一个基都会导致同一个线性映射有不同的变换矩阵。 -
可逆性:
线性映射是一个可逆的同构,当且仅当其变换矩阵 是方阵 ( ) 且可逆。Non-Invertible Transformations and Information Loss
2. 基变换矩阵
这是变换矩阵的一个特殊应用,用于在同一个向量空间内将一个向量的坐标从一个基转换到另一个基。这个过程等价于为恒等映射(
-
基变换矩阵 (
):
这个矩阵将坐标从一个新基转换到一个旧基 。它的列是新基向量在旧基下的坐标向量。 注意:如果“旧”基
是 中的标准基,则这个矩阵的列就是新基 的向量本身。 -
使用公式:
- 将坐标从新基 (
) 转换到旧基 ( ): - 将坐标从旧基 (
) 转换到新基 ( ):
- 将坐标从新基 (
3. 线性映射的基变换定理
Change-of-Basis Theorem
该定理提供了一个公式,用于在改变线性映射的定义域和陪域的基(坐标系)时,计算新的变换矩阵。
-
定理陈述:
给定一个线性映射,其中: - 一个“旧”输入基
和一个“新”输入基 ,都用于定义域 。 - 一个“旧”输出基
和一个“新”输出基 ,都用于陪域 。 - 原始的变换矩阵
(相对于旧基 和 )。
新的变换矩阵
(相对于新基 和 )由下式给出: 其中基变换矩阵定义为:
:定义域 内的基变换矩阵。它将坐标从新输入基 转换到旧输入基 。 :陪域 内的基变换矩阵。它将坐标从新输出基 转换到旧输出基 。
- 一个“旧”输入基
-
公式解释(变换的“路径”):
该公式表示对一个坐标向量进行的一系列三个操作。坐标的路径是。 - 第1步:
S(从在定义域中): 我们从一个向量在新输入基下的坐标 开始。我们应用 将这些坐标转换为旧输入基: 。 - 第2步:
AΦ(从基到基 ): 我们将原始变换矩阵 应用到现已用旧输入基 表示的坐标上。这得到了像在旧输出基 下的坐标: 。 - 第3步:
T⁻¹(从在陪域中): 结果是用旧输出基 表示的。为了用新输出基 表示它,我们必须应用 的逆。因为 从 转换到 ,所以必须使用 从 转换到 : 。
- 第1步:
4. 矩阵等价与相似
这些概念形式化了这样一种思想:不同的矩阵可以表示相同的底层线性映射,只是使用了不同的坐标系。
-
矩阵等价:
- 定义: 如果存在可逆矩阵
(在定义域中)和 (在陪域中)使得 ,则两个 矩阵 和 是等价的。 - 解释: 等价矩阵表示完全相同的线性变换
。它们仅仅是由于在定义域 和陪域 中选择了不同的基(坐标系)而对 的不同数值表示。
- 定义: 如果存在可逆矩阵
-
矩阵相似:
- 定义: 如果存在一个单一的可逆矩阵
使得 ,则两个方阵 的 和 是相似的。 - 解释: 相似性是等价性在自同态(
)上的一个特例,其中同一个空间既作为定义域又作为陪域,因此相同的基变换(即 )被应用于输入和输出坐标。
- 定义: 如果存在一个单一的可逆矩阵
5. 线性映射的复合
- 定理: 如果
和 是线性映射,它们的复合 也是一个线性映射。 - 矩阵表示: 复合映射的变换矩阵是各个变换矩阵的乘积,顺序与应用顺序相反:
第四部分:仿射空间与仿射子空间
虽然向量空间和子空间是基础,但它们受一个关键要求的限制:必须包含原点。仿射空间将这一思想推广到描述那些不一定穿过原点的几何对象,如直线和平面。
-
核心直观:向量空间 vs. 仿射空间
- 向量子空间是一条必须穿过原点的直线或平面(或更高维的等价物)。
- 仿射子空间是一条被平移过的直线或平面(或更高维的等价物),因此不再需要穿过原点。它是向量空间中的一个“平面”曲面。
-
仿射子空间的正式定义
向量空间
的一个仿射子空间 是一个可以表示为一个特定向量(一个点)和一个向量子空间之和的子集。 其中:
是一个特定的向量,通常称为平移向量或支撑点。它起到平移空间的作用。 是 的一个向量子空间,通常称为方向空间或相关的向量子空间。它定义了仿射子空间的方向和“形状”(直线、平面等)。
仿射子空间
的维度被定义为其方向空间 的维度。 -
几何示例:
中的一条直线: 穿过点 且方向向量为 的直线是一个仿射子空间。 这里,支撑点是 ,方向空间是1维向量子空间 。 中的一个平面: 包含点 且与向量 和 (线性无关)平行的平面是一个仿射子空间。 这里,支撑点是 ,方向空间是2维向量子空间 。
-
与线性系统解的联系(关键应用)
仿射子空间为线性系统的解集提供了完美的几何描述。
-
齐次系统
Ax = 0: 齐次系统的所有解的集合是的零空间,记为 。零空间永远是一个向量子空间。 -
非齐次系统
Ax = b: 非齐次系统(其中)的所有解的集合是一个仿射子空间。
回想通解公式:让我们将其映射到仿射子空间
的定义中: - 特解
作为平移向量 。 - 所有齐次解
的集合是方向空间 。这正是零空间 。
因此,
Ax = b的完整解集是仿射子空间:这意味着解集是零空间
被一个特解向量 平移后的结果。 - 特解
-
-
关键差异总结
| 特征 | 向量子空间 (U) |
仿射子空间 (L = p + U) |
|---|---|---|
| 必须包含原点? | 是 (0 ∈ U) |
否,除非 p ∈ U。 |
| 加法封闭? | 是。如果 u₁, u₂ ∈ U,则 u₁ + u₂ ∈ U。 |
否。通常,l₁ + l₂ ∉ L。 |
| 标量乘法封闭? | 是。如果 u ∈ U,则 cu ∈ U。 |
否。通常,cl₁ ∉ L。 |
| 几何示例 | 穿过原点的直线/平面。 | 任何被平移的直线/平面。 |
| 线性系统示例 | Ax = 0 的解集。 |
Ax = b 的解集。 |
- 仿射组合
- 一个相关的概念是仿射组合。它是一种系数之和为1的线性组合。
- 仿射子空间在仿射组合下是封闭的。一组点的所有仿射组合的集合构成了包含它们的最小仿射子空间(它们的“仿射包”)。
[[如何用仿射子空间 (Affine Subspace) 的结构来理解线性方程组Aλ = b的通解]]
- 一个相关的概念是仿射组合。它是一种系数之和为1的线性组合。
第五部分:超平面 (Hyperplanes)
超平面是将在2D空间中的线和3D空间中的平面的概念推广到任意维度向量空间的结果。它是一种极其重要且常见的特殊仿射子空间。
1. 核心直观
- 在2D空间 (
)中,超平面是一条线(1维)。 - 在3D空间 (
)中,超平面是一个平面(2维)。 - 在n维空间 (
)中,超平面是一个**(n-1)维**的“平坦”子空间。
它的关键功能是将整个空间“切片”成两个半空间,使其成为分类问题中理想的决策边界。
2. 超平面的两个等价定义
超平面可以用两种等价的方式定义:一种是代数的,一种是几何的。
定义1:代数定义(通过单个线性方程)
其中 d 是一个常数。
使用向量表示法,这个方程变得更加紧凑:
- 法向量
: 向量 被称为超平面的法向量。几何上,它与超平面本身垂直。 - 偏移量
d: 常数d决定了超平面距离原点的偏移量。- 如果
d = 0,超平面aᵀx = 0穿过原点,并且本身是一个**(n-1)维的向量子空间**。 - 如果
d ≠ 0,超平面不穿过原点,是一个真正的仿射子空间。
- 如果
定义2:几何定义(通过仿射子空间)
n维向量空间
其中:
是超平面上的任意一个特定点(支撑点)。 是一个维度为n-1的向量子空间(方向空间)。
3. 定义之间的联系
这两个定义是完全等价的。
- 从代数到几何 (
aᵀx = d→p + U):- 方向空间
U: 方向空间U是与原超平面平行且穿过原点的超平面。它是满足aᵀu = 0的所有向量u的集合。这个集合是法向量a的正交补,维度为 n-1。 - 支撑点
p: 我们可以通过找到方程aᵀx = d的任意一个特解来找到一个支撑点p。
- 方向空间
4. 机器学习中的超平面
超平面是许多机器学习算法的核心,最著名的是支持向量机 (SVM)。
- 作为决策边界: 在二元分类问题中,目标是找到一个能够最好地分隔属于两个不同类别的数据点的超平面。
- SVM 超平面: SVM 寻求找到一个由以下方程定义的最优超平面:
是权重向量,等价于法向量 a。b是偏置项,与偏移量d相关。
- 分类规则:
- 如果一个新的数据点
满足 ,它被分到一类(例如,正类)。 - 如果它满足
,它被分到另一类(例如,负类)。 - 这意味着一个点的分类取决于它位于超平面的哪一侧。SVM的目标是找到使这个分隔“间隔”尽可能宽的
w和b。
- 如果一个新的数据点
第六部分:仿射映射 (Affine Mappings)
我们已经确定,形式为 φ(x) = Ax 的线性映射总是保持原点不变(即 φ(0) = 0)。然而,许多实际应用,特别是计算机图形学,需要包括平移的变换,这会移动原点。这种更一般的变换类别被称为仿射映射。
1. 核心思想:一个线性映射后跟一个平移
一个仿射映射本质上是一个线性映射和一个平移的复合。
- 线性部分: 处理旋转、缩放、剪切和其他保持原点固定的变换。
- 平移部分: 将整个结果移动到空间中的一个新位置。
2. 正式定义
从向量空间 V 到向量空间 W 的映射 f: V → W 被称为仿射映射,如果它可以写成以下形式:
其中:
A是一个矩阵,表示变换的线性部分。 b是一个向量,表示平移部分。
与线性映射的区别:
- 如果平移向量
b = 0,仿射映射退化为纯粹的线性映射。 - 如果
b ≠ 0,则f(0) = A(0) + b = b,这意味着原点不再映射到原点,而是被移动到由b定义的位置。
3. 仿射映射的关键性质
虽然仿射映射通常不是线性的(因为 f(x+y) ≠ f(x) + f(y)),但它们保留了几个关键的几何性质。
-
直线映射为直线: 仿射映射将一条直线变换为另一条直线(或者在退化情况下,如果直线的方向在
A的零空间中,则变换为单个点)。 -
平行性被保留: 如果两条线是平行的,它们在仿射映射下的像也将是平行的。
-
长度比率被保留: 如果点
P是线段QR的中点,那么它的像f(P)将是像线段f(Q)f(R)的中点。 -
仿射组合被保留: 这是仿射映射最基本的代数性质。如果一个点
y是一组点xᵢ的仿射组合(即y = Σαᵢxᵢ且Σαᵢ = 1),那么它的像f(y)是像点f(xᵢ)的相同仿射组合:
4. 齐次坐标:统一变换的技巧
在计算机图形学等领域,用单一的矩阵乘法来表示所有变换(包括平移)是非常理想的。标准形式 Ax + b 需要乘法和加法,这对于复合多个变换很不方便。
齐次坐标通过增加一个额外的维度,巧妙地解决了这个问题,有效地将一个仿射映射变成了更高维空间中的一个线性映射。
-
工作原理:
- 一个n维向量
x = (x₁, ..., xₙ)ᵀ被表示为一个(n+1)维的齐次向量: - 一个仿射映射
f(x) = Ax + b由一个(n+1) × (n+1)的增广变换矩阵表示:这里, A是的线性部分, b是的平移向量。底行由零和一个一组成。
- 一个n维向量
-
统一的操作:
仿射变换现在可以用一次矩阵乘法完成:结果向量的前
n个分量正是所需的Ax + b,最后一个分量保持为1。 -
优势:
这种技术允许通过首先乘以它们各自的增广矩阵来复合一系列变换(例如,旋转、缩放、再平移)。得到的单一矩阵可以应用于所有点,极大地简化了复杂变换的计算和管理。
5. 总结
| 概念 | 线性映射 (Ax) |
仿射映射 (Ax + b) |
|---|---|---|
| 本质 | 旋转 / 缩放 / 剪切 | 线性变换 + 平移 |
| 保留原点? | 是, f(0) = 0 |
否, 通常 f(0) = b |
| 保留线性组合? | 是 | 否 |
| 保留什么? | 直线、平行性、线性组合 | 直线、平行性、仿射组合 |
| 表示法 | 矩阵 A |
矩阵 A 和向量 b |
| 齐次坐标形式 |
第三讲:解析几何:范数、内积、长度与距离、角度与正交性
第一部分:向量空间上的几何结构
在前面部分,我们建立了向量空间和线性映射的代数框架。现在,我们将为这些空间赋予几何结构,使我们能够形式化向量的长度、向量间的距离以及它们之间的角度等直观概念。这些概念由范数和内积来捕捉。
1. 范数 (Norms)
范数是向量“长度”或“大小”这一直观概念的形式化推广。
-
几何直观: 向量的范数是其长度,即从原点到该向量所代表的点的距离。
-
范数的正式定义:
向量空间上的一个范数是一个函数 ,它为每个向量 赋予一个非负实值 。该函数必须满足以下三个公理: -
正定性: 长度是正的,除非是零向量。
-
绝对齐次性: 缩放一个向量会以相同的因子缩放其长度。
-
三角不等式: 三角形的一边长度不大于另外两边长度之和。
配备了范数的向量空间称为赋范向量空间。
-
-
上的范数示例:
对于向量: -
-范数 (曼哈顿范数): 测量“城市街区”距离。 -
-范数 (欧几里得范数): 标准的“直线”距离。 **这是默认范数。**当我们写
而不带下标时,几乎总是指欧几里得范数。 -
-范数 (最大范数): 长度由向量的最大分量决定。
-
-
由范数导出的距离:
任何范数都自然地定义了两个向量之间的距离,即它们差向量的范数:
2. 内积 (Inner Products)
内积是一个比范数更基本的概念。它是一个函数,不仅允许我们定义欧几里得范数,还允许我们定义向量间的角度和正交性(垂直性)的概念。
-
动机: 内积是
中熟悉的点积的推广,点积定义为: -
内积的正式定义:
实向量空间上的一个内积是一个函数 ,它接收两个向量并返回一个标量。该函数必须是一个对称、正定的双线性映射,满足以下公理: - 双线性: 函数在每个参数中都是线性的。
- 对称性: 参数的顺序不影响结果。
- 正定性: 向量与自身的内积是非负的,并且仅当向量为零向量时才为零。
配备了内积的向量空间称为内积空间。
3. 桥梁:从内积到几何
内积是向量空间内欧几里得几何的基础。所有关键的几何概念都可以从中导出。
-
诱导范数:
每个内积都自然地定义(或诱导)一个范数,由下式给出:标准的欧几里得范数
正是由标准点积诱导的范数。 -
柯西-施瓦茨不等式:
它将两个向量的内积与它们的诱导范数联系起来,并为定义角度提供了基础。 -
由内积定义的几何概念:
- 长度:
- 距离:
- 角度: 两个非零向量
和 之间的角度 通过以下方式定义: - 正交性 (垂直性):
- 定义: 如果两个向量
和 的内积为零,则它们是正交的。我们记为 。 - 勾股定理: 如果
,则熟悉的勾股定理成立:
- 定义: 如果两个向量
- 长度:
第二部分:向量空间上的几何结构
1. 对称正定 (SPD) 矩阵与内积
在像
-
对称正定矩阵的定义:
一个方阵被称为对称正定 (SPD),如果它满足两个条件: - 对称性:
- 正定性: 对于每个非零向量
,二次型 严格为正。Quadratic Form
- 对称性:
-
中心定理:内积的矩阵表示
定理:这个函数是一个有效的内积,当且仅当矩阵
是对称且正定的。 解释:
- 该定理为有限维空间上所有可能的内积提供了通用配方。
中的标准点积是该定理最简单的情况,其中矩阵 是单位矩阵 : - 任何 SPD 矩阵
都可以用来定义一个新的、完全有效的内积 。
-
SPD 矩阵的性质
- 可逆性 (零空间平凡): SPD 矩阵总是可逆的。它的零空间只包含零向量。
- 正对角元素: SPD 矩阵的所有对角元素都严格为正。
-
回顾:内积 vs. 点积
- 内积
: 一般概念。 - 点积
: 具体示例,是由单位矩阵定义的内积。 - 欧几里得范数
: 由点积诱导的范数。
- 内积
第三部分:角度、正交性与正交矩阵
1. 角度与正交性
-
定义角度:
-
正交性:
- 定义: 两个向量
和 是正交的,如果它们的内积为零。记为 。 - 几何意义: 角度
(90°)。
- 定义: 两个向量
-
标准正交性 (Orthonormality):
- 两个向量
和 是标准正交的,如果它们既正交( )又是单位向量( , )。
- 两个向量
-
关键点:正交性取决于内积
- 两个向量是否正交完全取决于所选的内积。
2. 正交矩阵
-
定义:
一个方阵被称为正交矩阵,当且仅当其列构成一个标准正交集。 -
等价性质:
的列是标准正交的。
- 核心思想: 正交矩阵的逆矩阵就是其转置。
-
几何性质:保持长度和角度
由正交矩阵定义的线性变换 是一种刚体变换。 - 保持长度:
- 保持内积和角度:
- 保持长度:
-
实际意义与应用:
- 几何模型: 正交矩阵完美地模拟了空间中的旋转和反射。
- 数值稳定性: 涉及正交矩阵的算法(如 QR 分解)通常非常数值稳定。
- 坐标系变换: 从一个标准正交基到另一个的变换由一个正交矩阵描述。
第四部分:度量空间与距离的正式定义
度量 (metric) 形式化了任何集合元素之间“距离”的直观概念。
1. 度量函数 (Metric Function)
-
正式定义:
集合V上的一个度量是一个函数d : V × V → ℝ,它将一对元素(x, y)映射到一个实数d(x, y),并满足以下三个公理:- 正定性:
d(x, y) ≥ 0d(x, y) = 0当且仅当x = y
- 对称性:
d(x, y) = d(y, x)
- 三角不等式:
d(x, z) ≤ d(x, y) + d(y, z)
- 正定性:
-
度量空间 (Metric Space):
配备了度量d的集合V称为度量空间,记为(V, d)。
2. 联系:从内积到度量
- 定理: 由内积诱导的距离函数
d(x, y) = ||x - y||是一个度量。
3. 为什么度量的概念有用?
它允许我们在远超标准欧几里得几何的背景下测量“距离”。
- 推广: 适用于任何集合,包括:
- 字符串: 编辑距离是一个度量。
- 图: 图中两个节点之间的最短路径距离是一个度量。
- 函数: 我们可以定义度量来测量两个函数相距多“远”。
4. 空间层次总结
内积空间 → 赋范空间 → 度量空间 → 拓扑空间
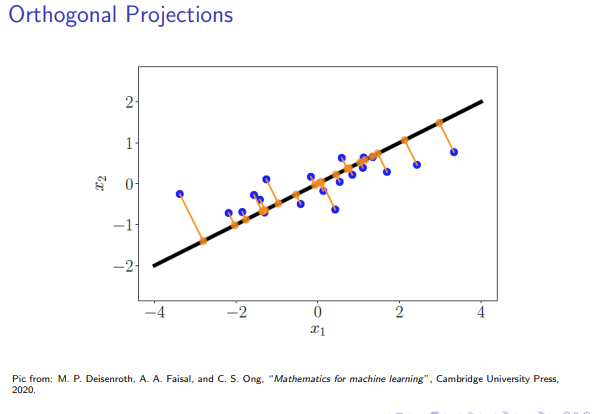
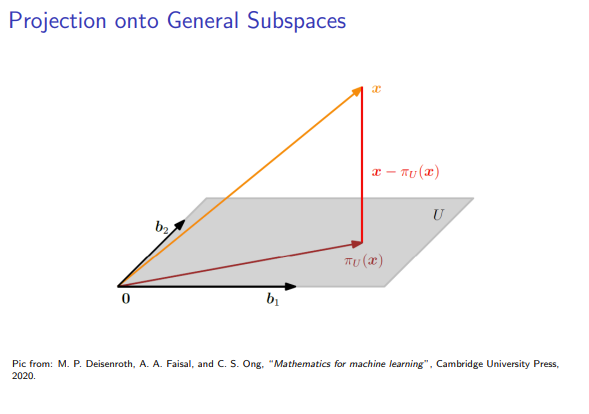
第五部分:正交投影
正交投影是一种基本操作,用于在给定子空间中找到与给定向量“最接近”的向量。
1. 正交投影的概念
令
这个投影
- 隶属属性:
- 正交属性:
2. 推导投影公式(法方程)
第1步:用基表示隶属属性
令
第2步:将正交属性表示为方程
第3步:组合并求解 λ
将第一个方程代入第二个方程:
得到法方程 (Normal Equation):
3. 正交投影算法
- 找到基: 找到子空间
的一个基。 - 构成基矩阵
B。 - 建立法方程: 计算
BᵀB和Bᵀx。 - 求解
λ。 - 计算投影
p: 使用公式p = Bλ。
4. 特殊情况:标准正交基
如果
- 法方程变为:
- 投影公式为:
- 矩阵
称为投影矩阵。
第四讲:解析几何:标准正交基、正交补、函数内积、正交投影、旋转
第一部分:标准正交基与正交补
1. 标准正交基
- 定义: 标准正交基是一种特殊的基,其中所有基向量相互正交,并且每个基向量都是单位向量。
- 形式化: 对于基
: - 正交性:
对于所有 。 - 归一化:
对于所有 。
- 正交性:
- 形式化: 对于基
- 正交基: 如果只满足正交性条件,则称为正交基。
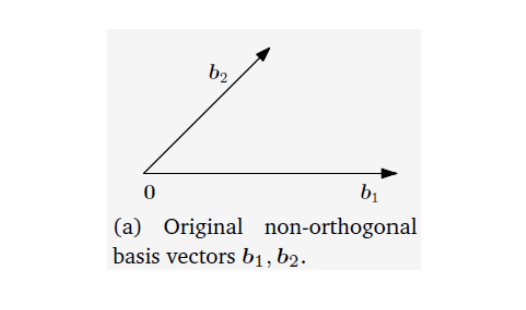
2. 格拉姆-施密特过程:构造标准正交基
格拉姆-施密特过程是一个将任何线性无关向量集(一个基)转换为相同子空间的标准正交基的算法。
- 目标: 给定一个基
,生成一个标准正交基 。 - 算法步骤:
- 初始化: 归一化第一个向量
得到 。 - 迭代与正交化: 对于后续的每个向量
:
a. 投影并相减: 从中减去其在已找到的标准正交向量 所张成的子空间上的投影,得到一个正交向量 。
$$ \mathbf{v}_k = \mathbf{a}k - \sum^{k-1} \langle \mathbf{a}_k, \mathbf{q}_j \rangle \mathbf{q}_j $$
b. 归一化: 归一化得到 。
$$ \mathbf{q}_k = \frac{\mathbf{v}_k}{|\mathbf{v}_k|} $$
- 初始化: 归一化第一个向量
3. 正的概念从单个向量推广到整个子空间。
-
定义 (正交补): 令
是向量空间 的一个子空间。 的正交补,记为 ,是 中所有与 中每个向量都正交的向量的集合。 -
空间分解 (直和): 整个空间
可以被唯一地分解为子空间 与其正交补 的直和。这意味着 和 的交集只有零向量,并且它们的维度之和等于 的维度。 -
向量分解 (正交分解): 基于空间的直和分解,
中的任何一个向量 都可以被唯一地分解为一个在 中的分量和一个在 中的分量之和。 - 概念层面:
- 基层面表示: 在计算上,这个分解通过找到
关于 的基和 的基的唯一坐标来实现。 其中, 是 的一组基, 是 的一组基,而 是唯一的标量坐标。 - 分量
正是 在子空间 上的正交投影。
- 概念层面:
第二部分:函数内积、正交投影与旋转
1. 函数的内积
- 定义: 对于在区间
上的连续函数空间,两个函数 和 之间的标准内积定义为积分: - 诱导的几何性质:
- 长度 (范数):
- 正交性: 如果
,则两个函数正交。
- 长度 (范数):
- 意义: 这种推广是傅里叶级数的数学基础。Fourier Series
2. 正交投影
正交投影是解决最小二乘问题的几何基础。
- 概念: 向量
在子空间 上的正交投影是 中唯一的向量 ,使得误差向量 与整个子空间 正交。 - 投影公式 (回顾):
- 构成基矩阵
。 - 求解法方程
得到 。 - 计算投影
。
- 构成基矩阵
- Projection Matrix:
。
3. 旋转
- 定义: 旋转是一种保持物体形状和大小的线性变换。
- 矩阵性质: 一个矩阵
表示纯旋转,如果它满足两个条件: - 正交性:
(保持长度和角度)。 - 保持方向:
(行列式为-1的表示反射)。
- 正交性:
- 2D 旋转: 在2D平面中逆时针旋转角度
的矩阵是: - 群结构: 所有
旋转矩阵的集合构成一个数学群,称为特殊正交群,记为 。
第三部分:正交投影详解
投影是一类至关重要的线性变换,广泛应用于图形学、编码理论、统计学和机器学习中。
1. 正交投影的重要性与概念
- 在机器学习中的动机: 在机器学习中,我们经常处理难以分析或可视化的多维数据。一个关键的洞见是,大部分相关信息通常包含在一个维度低得多的子空间内。
- 目标(维度约减): 通过将多维数据投影到一个精心选择的低维“特征空间”,我们可以简化问题、降低计算成本并提取有意义的模式。其目标是在执行此投影的同时,最小化信息损失。
- 什么是正交投影?
- 它是一种线性变换,将一个向量从高维空间“投射”到低维子空间上。
- 它之所以是“正交”的,是因为它通过最小化原始数据与其投影图像之间的误差(距离)来最大可能地保留信息。
- 这一特性使其成为线性回归、分类和数据压缩的核心。
2. 投影的正式定义与性质
- 代数定义(幂等性): 一个线性映射
如果应用两次与应用一次的效果相同,则被称为投影。这被称为幂等性。 - 矩阵形式: 如果一个方阵
满足 ,那么它就是一个投影矩阵。
- 矩阵形式: 如果一个方阵
- 几何定义(最近点): 向量
在子空间 上的正交投影 是 中离 最近的那个唯一的点。 - 这个“最近点”条件等价于正交性条件:差向量
必须与子空间 中的每一个向量都正交。
- 这个“最近点”条件等价于正交性条件:差向量
3. 投影到一维子空间(直线)

我们从最简单的情况开始推导投影公式:将一个向量投影到一条直线上。除非另有说明,我们都假设使用标准的点积作为内积。
- 设定: 令
为由非零基向量 张成的一维子空间(一条过原点的直线)。 - 推导过程: 投影
必须是 的一个标量倍,即 。通过正交条件 ,我们可以解出坐标 。 - 一维投影的最终公式:
- 坐标:
- 投影向量:
- 投影矩阵:
- 坐标:
4. 投影到一般子空间

用于一维投影的三步法可以推广到任何 m 维子空间
- 设定: 假设
有一个基 ,构建基矩阵 。 - 推导过程: 投影
。通过正交条件 ,我们得到正规方程 (Normal Equation)。 - 最终公式:
- 正规方程:
- 坐标:
- 投影向量:
- 投影矩阵:
- 正规方程:
拓展:子空间之间的投影Projections between Subspaces
5. 核心应用 I:Gram-Schmidt正交化
Gram-Schmidt过程是构造一组标准正交基的经典算法,其核心思想就是反复利用正交投影。
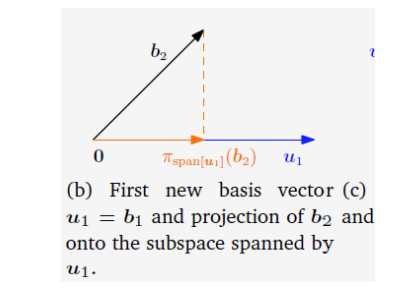
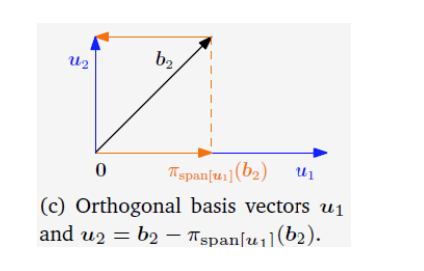
-
目标: 将一组线性无关的向量
转换为一组正交向量 ,并且两组向量张成相同的子空间。 -
迭代构造法:
- 第一步: 选择第一个向量作为新基的起点。
- 后续步骤 (k=2 to n): 对于每一个新的向量
,减去它在已经构造好的正交子空间 上的投影。剩下的分量就必然与该子空间正交。 由于 已经正交,投影可以更简单地写成:
- 第一步: 选择第一个向量作为新基的起点。
-
获得标准正交基 (ONB): 在每一步得到正交向量
后,对其进行标准化即可。 -
示例: 对
中的基 进行正交化。 - 最终得到正交基
。
拓展:Cholesky分解
6. 核心应用 II:投影到仿射子空间
到目前为止,我们讨论的都是投影到过原点的子空间。现在我们将其推广到不过原点的仿射子空间(例如,不过原点的直线或平面)。
-
定义: 一个仿射子空间
可以表示为 ,其中 是一个支持点(位移向量), 是一个与 平行的、过原点的方向子空间。 -
求解策略:平移-投影-移回
- 平移至原点: 从待投影点
和仿射空间 中都减去支持点 。这使得问题转化为将新向量 投影到我们熟悉的方向子空间 上。 - 标准投影: 计算向量
在子空间 上的正交投影 。 - 移回原位: 将投影结果平移回原来的位置,即加上支持点
。
- 平移至原点: 从待投影点
-
最终公式:
-
数学证明: 我们要找到点
来最小化距离 。 - 因为
,所以它可以写成 ,其中 。 - 最小化
就等价于最小化 。 - 根据定义,使这个距离最小的
正是向量 在子空间 上的投影,即 。 - 因此,最近点
。
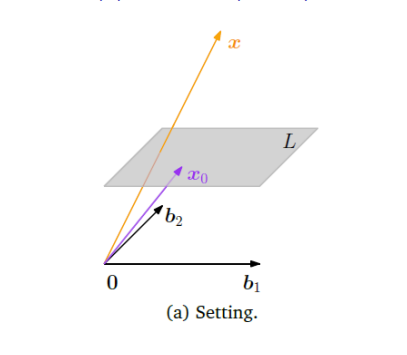
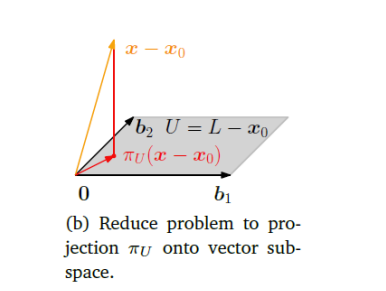
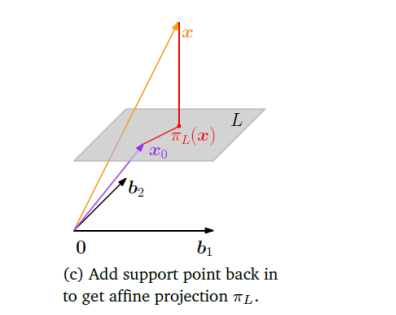
- 因为
-
点到仿射子空间的距离:
这表明,点到仿射空间的距离,等于平移后的点到其方向子空间的距离。
7. 核心应用 III:投影与最小二乘解
Moore Penrose Pseudo inverse
正交投影为求解无解的线性方程组 Ax=b 提供了一个强大的几何框架,这构成了最小二乘法 (Least Squares Method) 的基础。
- 问题的根源: 当方程
Ax=b无解时,从几何上看,这意味着向量b不在矩阵A的列空间Col(A)内。 - 解决思路: 既然无法在
Col(A)中找到一个点等于b,我们就退而求其次,寻找一个Col(A)中离b最近的点。 - 投影是答案: 根据定义,这个“最近点”正是
b在Col(A)上的正交投影,我们记为。 - 求解新方程: 我们现在求解一个新的、必有解的方程:
这个方程的解 就是原始问题的最小二乘解。 - 为什么叫“最小二乘”? 因为这个解
能够使误差向量的长度平方 达到最小。这个长度的平方就是各项误差的平方和 (sum of squares),因此得名。
第四部分:旋转详解 (Rotations)
旋转是继投影之后的另一类重要的线性变换,它在几何学、计算机图形学和机器人学中扮演着核心角色。
1. 旋转的基本概念
- 与正交变换的关系: 旋转是正交变换的一个特例。正交变换的核心特性是它们在变换过程中保持向量的长度和向量间的夹角不变。旋转完美地符合这一特性。
- 定义: 一个旋转是一个线性函数,它将一个平面(或空间)围绕一个固定的原点旋转一个特定的角度
。 - 方向约定: 按照惯例,一个正角度
对应于逆时针 (counter-clockwise) 旋转。 - 核心性质: 旋转只改变向量的方向,不改变其到原点的距离。
2. R² 中的旋转
2.1 R² 旋转矩阵的推导:两种视角
视角一:基变换 (The "Columns are Transformed Basis Vectors" View)
这是从线性变换本质出发的标准推导方法。
- 目标: 找到一个矩阵
,当它乘以一个向量 时,能够将该向量围绕原点逆时针旋转 角。 - 关键思想: 一个线性变换矩阵的列向量,正是标准基向量经过该变换后的新坐标。
- 推导步骤:
- 确定标准基向量: 在
中,标准基是 和 。 - 旋转基向量:
- 将
旋转 角,新坐标是 。 - 将
旋转 角,新坐标是 。
- 将
- 构建旋转矩阵: 将变换后的基向量作为列,构成旋转矩阵。
- 确定标准基向量: 在
视角二:极坐标与三角恒等式 (The "Direct Geometric" View)
这是一个更直接的几何证明,不依赖于基变换的思想。
- 表示向量: 将任意向量用极坐标表示:
。 - 表示旋转: 将该向量旋转角度
,其角度变为 。新坐标 为: - 应用和角公式:
- 写成矩阵形式:
2.2 R² 旋转的应用与注意事项
- 坐标系依赖性: 上述推导的
只直接适用于在标准笛卡尔坐标系下表示的向量。 - 在非标准坐标系中旋转向量: 如果你的向量坐标
是在某个非标准基 下给出的,正确的做法是: - 基变换到笛卡尔坐标:
- 用标准矩阵旋转:
- (可选)变换回原基:
- 基变换到笛卡尔坐标:
- 旋转一个向量空间: 要旋转整个向量空间,只需旋转其所有基向量即可。如果一个空间的基由矩阵
的列给出,那么旋转后的新基矩阵为 。
3. R³ 中的旋转
三维空间中的旋转比二维更复杂,因为它必须围绕一个旋转轴 (axis of rotation) 进行。
- 定义: 在
中,旋转是围绕一条穿过原点的直线(轴)进行的。该轴上的所有点在旋转过程中保持不变。 - 构建任意3D旋转矩阵: 一个通用的3D旋转矩阵
可以通过确定标准基 旋转后的新位置 来构建,这些新向量必须保持标准正交性。
3.1 3D旋转的方向约定:右手定则
为了定义“逆时针”旋转,我们使用右手定则 (Right-Hand Rule):
- 规则: 将你的右手大拇指指向旋转轴的正方向。你其余四指弯曲的方向,就是正角度(逆时针) 的旋转方向。
3.2 沿坐标轴的基本旋转
任何复杂的3D旋转都可以分解为沿三个主坐标轴(x, y, z)的一系列基本旋转。
-
绕 x 轴 (
) 旋转 - 描述: x 坐标保持不变,旋转发生在 yz 平面。
- 矩阵:
-
绕 y 轴 (
) 旋转 - 描述: y 坐标保持不变,旋转发生在 zx 平面。
- 矩阵:
-
绕 z 轴 (
) 旋转 - 描述: z 坐标保持不变,旋转发生在 xy 平面。
- 矩阵:
3.3 3D基本旋转矩阵的三角证明
- 绕 x 轴: 在 yz 平面中,令
。旋转 角后,新坐标为 和 。通过和角公式展开,并保持 ,即可推导出 矩阵。 - 绕 z 轴: 在 xy 平面中,令
。旋转 角后,新坐标为 和 。展开后即可推导出 矩阵。 - 绕 y 轴 (特殊情况):
- 根据右手定则,大拇指指向+y,四指弯曲方向是从 z 轴到 x 轴。
- 因此,从
x到z的旋转被视为负角度。或者说,要实现一个正角度的旋转,新角度应该是ϕ-θ而不是ϕ+θ。 - 这解释了为什么
矩阵中 sinθ的符号与其他两个矩阵不同。
3.4 3D序贯旋转 (Sequential Rotations)
- 顺序的重要性: 在三维及更高维度中,旋转操作不满足交换律 (not commutative)。即
RxRy ≠ RyRx。因此,旋转的顺序至关重要。 - 矩阵乘法顺序: 旋转操作是从右向左依次施加的。如果要先绕x轴,再绕y轴,最后绕z轴旋转向量
x,组合旋转矩阵的计算方式是:
4. 高维空间 (Rⁿ) 中的旋转:吉文斯旋转 (Givens Rotation)
- 核心思想: 在 n 维空间中的任何旋转,都可以被看作是在一个二维平面内的旋转,同时保持其余
个维度不变。 - 定义:吉文斯旋转
- 一个在
(i, j)平面中进行旋转的 n 维旋转矩阵,记为。 - 它的结构是一个被修改过的单位矩阵。具体来说,
是一个 n x n矩阵,其形式如下: - 这个矩阵在绝大多数位置上是单位矩阵,只在第
i行i列、i行j列、j行i列、j行j列这四个位置上,嵌入了一个标准的二维旋转矩阵:
- 一个在
- 实践中的应用:
- 在实际算法中(如QR分解),我们通常不是预先设定
θ,而是根据需求反向计算出cosθ和sinθ的值,以达到特定目的,例如将一个向量在特定维度上的分量清零。
- 在实际算法中(如QR分解),我们通常不是预先设定
5. 旋转的通用性质
- 正交性: 旋转矩阵
R都是正交矩阵,满足RᵀR = I,即Rᵀ = R⁻¹。 - 保距性:
||Rx - Ry|| = ||x - y||,旋转不改变点与点之间的距离。 - 保角性: 旋转不改变向量之间的夹角。
- 交换律:
- 在 R² 中,旋转满足交换律:
R(φ)R(θ) = R(θ)R(φ)。 - 在 R³ 及更高维度中,旋转不满足交换律。
- 在 R² 中,旋转满足交换律:
第五讲:矩阵分解 (Matrix Decompositions)
第一部分:行列式与迹 (Determinant and Trace)
在深入研究复杂的矩阵分解之前,我们首先需要掌握两个描述方阵特性的基本标量:行列式和迹。
1. 行列式 (Determinant)
行列式是线性代数中的一个核心概念,它将一个方阵映射到一个唯一的实数,这个实数蕴含了关于该矩阵和其所代表的线性变换的重要信息。
- 定义与记号:
- 行列式只为方阵 (
) 定义。 - 记号为
或 (注意不要与绝对值混淆)。
- 行列式只为方阵 (
1.1 行列式、可逆性与秩
行列式最直接、最重要的应用就是判断一个方阵是否可逆,以及它是否是满秩的。这三者是等价的。
-
核心定理: 对于一个方阵
,以下三个命题是等价的: 是可逆的 (invertible)。 的行列式不为零 ( )。 是满秩的 (full rank),即 。
-
证明思路
det(A) ≠ 0 ⇔ rk(A) = n:- (⇒) 如果
,根据之前的定理,我们知道 是可逆的。而一个 矩阵可逆的充要条件就是它是满秩的,因此 。 - (⇐) 如果
,这意味着 的行(或列)向量线性无关。通过高斯消元法(一系列不改变行列式非零性质的行操作),我们可以将 化为一个上三角矩阵 U。因为是满秩的,所以 U的对角线上有n个主元 (pivots),所有对角元都非零。而三角矩阵的行列式是其对角元的乘积,所以。由于行变换不改变行列式的非零性,因此 也必然不为零。
- (⇒) 如果
1.2 行列式的几何意义:体积与方向
行列式最深刻的几何意义是它代表了由矩阵的列向量(或行向量)所张成的平行多面体 (parallelepiped) 的有向体积 (signed volume)。
-
体积缩放因子: 行列式的绝对值
代表了由矩阵 所代表的线性变换对“体积”的缩放比例。一个单位立方体(由标准基向量张成,体积为1)经过 变换后,会变成一个由 的列向量张成的平行多面体,其体积恰好是 。 - 二维:
是平行四边形的面积。 - 三维:
是平行六面体的体积。 - 如果
,意味着空间被“压扁”到更低的维度(例如,一个三维物体被拍扁成一个平面或一条线),体积为零,此时矩阵不可逆。
- 二维:
-
方向性 (Orientation): 行列式的符号
描述了变换是否保持或翻转了空间的方向。 - 大小:
描述了体积的缩放比例。 - 符号:
描述了变换是否保持或翻转了空间的方向。 - 正行列式 (
det(A) > 0): 保持方向。变换后的基向量组与原始标准基向量组具有相同的“手性”(例如,在中都是右手系)。在 中,从第一个列向量到第二个列向量是逆时针旋转。 - 负行列式 (
det(A) < 0): 翻转方向。变换后的基向量组的手性与原始相反(例如,从右手系变成了左手系)。在中,从第一个列向量到第二个列向量是顺时针旋转,如同照镜子一样。 - 列交换与符号: 每交换矩阵的两列(或两行),行列式的符号就会反转一次。奇数次交换导致方向翻转,偶数次交换保持方向不变。
- 正行列式 (
- 大小:
1.3 行列式的计算
计算行列式有多种方法,适用于不同类型和阶数的矩阵。
-
低阶矩阵公式:
- 1x1 矩阵:
- 2x2 矩阵:
- 3x3 矩阵: 可以使用 萨吕法则 (Sarrus' rule) 进行计算。
- 1x1 矩阵:
-
三角矩阵:
对于任何上三角或下三角矩阵,其行列式等于对角线上所有元素的乘积。 -
拉普拉斯展开 (Laplace Expansion):
这是一个递归计算高阶行列式的通用方法,可将矩阵的行列式降解为多个 子矩阵的行列式计算。 - 沿第 j 列展开:
其中,
是从矩阵 中移除第 行和第 列后得到的子矩阵。 - 沿第 j 列展开:
-
分块矩阵 (Block Matrix):
当一个矩阵可以被划分为几个子矩阵块时,可以利用其结构简化行列式的计算。假设我们有一个分块矩阵: 其中
和 都是方阵。 计算公式:
-
如果
是可逆的: 这里的
称为 在 中的 舒尔补 (Schur Complement)。 -
如果
是可逆的: -
特殊情况 (分块三角矩阵):
如果或 ,矩阵呈现分块三角形式: 此时,行列式为左上角和右下角两个对角块行列式的乘积:
-
1.4 行列式的重要性质
设
- 乘法性质:
- 转置不变性:
- 逆矩阵: 如果
可逆, - 相似矩阵: 如果
和 相似(即 ),那么 。 - 标量乘法:
- 行/列操作:
- 交换两行或两列,行列式变号。
- 将某一行或某列的倍数加到另一行或另一列上,行列式不变。
1.5 行列式的理论与实践作用
- 历史角色: 历史上,行列式是分析矩阵可逆性和求解线性方程组(如克拉默法则)的核心手动工具。
- 现代计算: 在现代数值计算中,对于大规模矩阵,直接计算行列式(特别是通过拉普拉斯展开)的计算成本极高。高斯消元法成为了更受青睐的工具。它不仅可以求解方程组和求逆,还可以高效地计算行列式(通过将矩阵化为三角形式)。
- 理论重要性: 尽管在数值计算中的直接应用减少,行列式在理论层面仍然至关重要。它对于定义特征多项式、理解特征值和特征向量是不可或缺的,这些概念是现代科学与工程的基石。
2. 迹 (Trace)
迹是方阵的另一个重要标量,定义比行列式简单得多。
-
定义: 方阵
的迹是其主对角线上所有元素的和。 -
重要性:
- 迹等于矩阵所有特征值之和,在谱方法和系统稳定性分析中非常有用。
- 在机器学习和量子力学中,迹用于计算期望值和定义密度矩阵。
2.1 迹的性质
设
- 线性性:
和 。 - 单位矩阵:
- 循环不变性 (Cyclic Property):
- 对于
,有 。 - 推论:
。

- 对于
- 基无关性 (Basis-Independence):
- 迹对于相似变换是不变的。如果
,那么 。 - 这意味着一个线性变换的迹是一个内在属性,不随坐标基的选择而改变。
- 迹对于相似变换是不变的。如果
3. 特征多项式 (Characteristic Polynomial)
行列式和迹共同构成了定义特征多项式的基础,这是计算矩阵特征值的关键工具。
- 定义: 对于
,其特征多项式 是: 这是一个关于 的 n 次多项式。 - 与行列式和迹的关系:
- 多项式的常数项是
。 项的系数与迹相关: 。
- 多项式的常数项是
- 核心应用:
- 特征值: 特征多项式的根(即方程
的解)就是矩阵 的特征值。
- 特征值: 特征多项式的根(即方程
第二部分:特征值与特征向量 (Eigenvalues and Eigenvectors)
特征值和特征向量(简称“特征分析”)是线性代数中威力最强大的工具之一。它提供了一种全新的视角来理解和刻画一个方阵及其所代表的线性变换,揭示了变换最本质、最核心的特性。
1. 特征值与特征向量的定义与几何意义
1.1 定义
- 动机: 对于一个给定的线性变换(由矩阵
A代表),我们特别关心那些方向保持不变的特殊向量。当变换作用于这些向量时,它们只会被拉伸或压缩,而不会发生方向偏转。 - 特征值方程 (Eigenvalue Equation):
对于一个方阵,如果存在一个标量 和一个非零向量 ,满足以下方程: 那么: 被称为矩阵 的一个特征值 (Eigenvalue)。 被称为对应于特征值 的一个特征向量 (Eigenvector)。
1.2 几何意义:变换下的“不变方向”
- 一般向量 vs. 特征向量:
- 当一个线性变换
作用于一个普通向量时,该向量的大小和方向通常都会改变。 - 当
作用于一个特征向量 时,它的方向保持不变(或完全反向),仅仅是在这个方向上被拉伸或压缩了 倍。 - 如果
,向量被拉长。 - 如果
,向量被缩短。 - 如果
,向量的方向被完全翻转(180°),并根据 进行缩放。 - 如果
,向量保持不变(是变换的“不动点”)。 - 如果
,向量被“压扁”到零向量。
- 如果
- 当一个线性变换
- 示例:
对于矩阵: - 特征向量: 取
。计算 。向量 的方向不变,只是被拉长了3倍。因此, 是一个特征值, 是其对应的特征向量。 - 非特征向量: 取
。计算 。结果向量的方向发生了偏转,所以 不是一个特征向量。
- 特征向量: 取
1.3 特征向量的非唯一性
- 如果
是一个特征向量,那么任何与它共线 (collinear) 的非零向量 (其中 ) 也是对应于同一个特征值 的特征向量。 - 证明:
- 结论: 特征向量定义的不是一个单一的向量,而是一个方向,即一条穿过原点的直线。这条直线上的所有非零向量都是具有相同特征值的特征向量。
2. 特征值的计算
2.1 计算原理与特征方程
如何系统地找到一个矩阵的特征值?这需要我们将特征值方程转化为一个我们熟悉的问题。
-
核心思想: 将特征值方程
变形。 -
这个方程
是一个标准的齐次线性方程组。我们寻找的是它的非平凡解 (nontrivial solution),因为根据定义,特征向量 不能是零向量。 -
特征值的等价刻画定理: 对于
和 ,以下四个命题是完全等价的: 是 的一个特征值。 - 方程
存在一个非零解 。 - 矩阵
是奇异的 (singular),即它是不可逆的,或者说它的秩小于n: 。 - 矩阵
的行列式为零: 。
-
计算方法: 第四个命题为我们提供了计算特征值的具体方法。
是一个关于 的多项式,被称为特征多项式 。因此: 一个标量
是矩阵 的特征值,当且仅当它是特征多项式 的一个根。
2.2 计算步骤示例
给定矩阵
第一步:求解特征多项式
我们计算特征多项式
第二步:计算特征值
令
第三步:计算特征向量与特征空间
对于每一个特征值,我们求解方程
-
对于
: -
对于
:
3. 特征分析的核心概念
3.1 特征空间 (Eigenspace)
- 对于一个特定的特征值
,所有与之对应的特征向量,再加上零向量,共同构成了一个向量子空间。这个子空间被称为对应于 的特征空间,记为 。 。
3.2 代数重数与几何重数 (Algebraic and Geometric Multiplicity)
- 代数重数 (Algebraic Multiplicity): 一个特征值
作为特征多项式的根出现的次数。 - 几何重数 (Geometric Multiplicity): 一个特征值
对应特征空间 的维度。
重要关系: 对于任何一个特征值
3.3 特征向量的线性无关性
定理 1: 如果一个
更一般的定理 (Theorem 2): 如果一个
- 推论: 如果矩阵有
个不同的特征值,我们保证可以找到至少 个线性无关的特征向量。
3.4 谱 (Spectrum)
- 一个矩阵
的所有特征值的集合被称为 的谱 (spectrum),记为 。
4. 特征分析的几何直观
特征分析不仅是代数计算,它还提供了强大的几何直观,帮助我们理解线性变换的本质。
4.1 变换的分解:沿特征向量方向的拉伸
假设一个
- 分解: 空间中任何一个向量
都可以唯一地表示为这些特征向量的线性组合: - 变换: 当矩阵
作用于 时,变换会独立地作用在每一个特征向量分量上: - 直观解释: 线性变换
的作用,可以被看作是将向量 沿着它的各个特征向量方向进行分解,然后在每个特征方向上独立地进行拉伸或压缩(缩放因子即为对应的特征值 )。
4.2 示例1:压缩与拉伸 (保积变换)
考虑矩阵
- 特征值与特征向量:
对应特征向量 (水平方向)。 对应特征向量 (垂直方向)。
- 几何效应:
- 变换将所有向量在水平方向上压缩为原来的一半。
- 变换将所有向量在垂直方向上拉伸为原来的两倍。
- 行列式:
。这意味着该变换是保面积的:任何图形经过此变换,其面积保持不变。
4.3 示例2:投影 (降维变换)
考虑矩阵
- 特征值与特征向量:
对应特征向量 。 对应特征向量 。
- 几何效应:
- 任何在
方向上的分量,其缩放因子为0,意味着被**“压扁”或“消除”**。 - 任何在
方向上的分量,被拉伸为原来的两倍。 - 最终效果是将整个二维平面投影到直线
上。
- 任何在
- 行列式:
。这意味着该变换将二维图形的面积压缩为零(降维到一条线上)。
5. 亏损矩阵与广义特征向量 (Defective Matrices)
5.1 定义
- 一个
的方阵 如果它没有 个线性无关的特征向量,则被称为亏损矩阵 (Defective Matrix)。 - 备注: 亏损的根本原因是至少存在一个特征值,其几何重数 < 代数重数。因此,亏损矩阵必然有重复的特征值。
5.2 广义特征向量 (课程范围外)
当一个矩阵是亏损的,我们无法找到一组由特征向量构成的基。为了处理这种情况,需要引入广义特征向量 (Generalized Eigenvectors) 的概念来构建一个完整的基(称为若尔当基 Jordan Basis)。
- 若尔当链 (Jordan Chain): 对于一个代数重数为
但几何重数为 的特征值 ,我们可以构建一个链条: 是一个普通特征向量: 是一个广义特征向量: - ...
是一个广义特征向量:
- 变换作用: 矩阵
在这个链条上的作用是缩放与剪切 (shearing) 的混合: 。
6. 总结:线性无关特征向量的数量
对于一个
-
如果
有 个不同的特征值: - 那么它一定有
个线性无关的特征向量。 - 此时
不是亏损的。
- 那么它一定有
-
如果
有重复的特征值 (即不同的特征值数量 ): - 我们保证至少有
个线性无关的特征向量(每个不同特征值至少贡献一个)。 - 线性无关特征向量的总数最多为
。 - 总数是否达到
,取决于每一个重复特征值的几何重数是否等于其代数重数。 - 如果存在任何一个特征值,其几何重数小于其代数重数,那么矩阵
就是亏损的,其线性无关特征向量的总数将严格小于 。
- 我们保证至少有
7. 谱定理与对称矩阵
到目前为止,我们讨论了适用于所有方阵的特征分析。然而,当矩阵具有特定结构时,例如对称性,特征分析会展现出非常优美和强大的性质。这些性质由谱定理所概括。
7.1 对称正定/半正定矩阵
在介绍谱定理之前,我们先引入一类非常重要的对称矩阵。
定理: 对于任何矩阵
是对称的 (Symmetric)。 是半正定的 (Positive Semidefinite)。
补充说明: 如果矩阵
证明:
- 对称性:
- 半正定性: 对于任意非零向量
: 由于向量的 范数的平方总是非负的,所以 是半正定的。 - 正定性 (当
时):
如果,那么齐次方程 只有唯一解 。因此,对于任何 ,都有 。
这意味着。所以, 对所有 成立,故 是正定的。
7.2 谱定理 (Spectral Theorem)
谱定理: 如果一个矩阵
- 所有特征值都是实数。
- 存在一个由
的特征向量组成的标准正交基 (Orthonormal Basis) 来张成整个空间 。 是可正交对角化的 (Orthogonally Diagonalizable)。
谱定理的证明要点:
-
性质1:特征值为实数
- 设
是一个(可能为复数)的特征值, 是对应的特征向量。则 。 - 两边左乘其共轭转置
: 。 - 因为
是实对称矩阵 ( ),所以 是一个实数。 - 同时,
也是一个正实数。 - 由于
,所以 必须是实数。
- 设
-
性质2:存在标准正交基
- 不同特征值对应的特征向量正交: 如果
且 ,其中 ,那么可以证明 。 - 相同特征值对应的特征空间: 对于实对称矩阵,任何特征值的几何重数都等于其代数重数。这意味着我们总能找到足够多的线性无关的特征向量。对于重根特征值对应的特征空间,我们可以使用 格拉姆-施密特 (Gram-Schmidt) 正交化方法来构造一组标准正交基。
- 将所有特征空间的正交基合并起来,就构成了整个
空间的一个标准正交基。
- 不同特征值对应的特征向量正交: 如果
7.3 正交对角化 (Orthogonal Diagonalization)
谱定理的第三点通常以矩阵分解的形式呈现,这是其最重要的应用之一。
谱定理 (矩阵形式): 任何一个实对称矩阵
其中:
是一个正交矩阵 ( ,即 )。 的列由 的标准正交特征向量构成。 (大写Lambda) 是一个对角矩阵,其对角线上的元素是与 中特征向量一一对应的实数特征值。
7.4 谱分解 (Spectral Decomposition)
正交对角化还可以写成一种“求和”形式,称为谱分解。
谱分解: 任何一个实对称矩阵
其中:
是第 个特征值。 是对应的单位长度(标准正交)的特征向量。 - 每一项
都是一个秩为1的对称矩阵,可以看作是向 方向的投影操作,并按 进行缩放。 - 直观意义: 任何对称变换都可以被分解为一系列在相互正交方向上的投影和拉伸操作的叠加。
对称矩阵的几何变换 (Geometric transformation of symmetric matrices)
7.5 示例:对称矩阵的正交对角化
考虑对称矩阵
-
求特征值与特征向量:
。 - 特征值为
。 - 对应的特征向量为
。(注意它们是正交的)
-
单位化特征向量:
-
构造 Q 和 Λ:
-
正交对角化:
。 -
谱分解:
8. 特征值与矩阵不变量的关系
特征值与矩阵的两个重要不变量——行列式 (Determinant) 和 迹 (Trace) 之间存在着深刻的联系。
8.1 特征值与行列式
定理: 任何一个方阵
证明思路 (对于可对角化矩阵):
- 如果
可对角化,则 。 。 - 因为
,所以 。 - 对角矩阵
的行列式就是其对角元素的乘积,即所有特征值的乘积。
几何直观: 行列式描述了线性变换对“体积”(或面积)的缩放比例。特征值则描述了在各个特征方向上的缩放比例。变换对总体积的缩放,等于在各个独立方向上缩放比例的乘积。
8.2 特征值与迹
定理: 任何一个方阵
证明思路 (对于可对角化矩阵):
- 利用迹的循环性质:
。 。 - 令
,则 。 - 对角矩阵
的迹就是其对角元素的和,即所有特征值的和。
非对称矩阵的补充说明:
尽管非对称矩阵不一定满足谱定理的优美性质(如特征值不一定是实数,特征向量不一定正交),但只要它们是可对角化的,上述关于变换分解、行列式、迹的结论依然成立。对称矩阵的特殊之处在于它保证了可对角化,并且是用一种更稳定、更具几何美感的正交矩阵来实现的。
拓展:鞍点的最速逃离方向 (The fastest escape direction for the stationed point)
9. Cholesky 分解 (Cholesky Decomposition)
Cholesky 分解是另一类重要的矩阵分解,它专门针对对称正定矩阵 (Symmetric Positive Definite, SPD),并且在数值计算和机器学习中因其高效性而被广泛使用。
9.1 定义与动机
对于一个正实数(例如 9),我们可以通过开方运算将其分解为两个相同的部分(
它将一个对称正定矩阵
9.2 Cholesky 分解定理
定理 (Cholesky Decomposition): 任何一个对称正定矩阵
其中:
是一个下三角矩阵 (lower triangular matrix)。 的主对角线元素均为正数。 被称为 的 Cholesky 因子 (Cholesky factor)。 - 对于每一个
,这个分解是唯一的。
重要前提: Cholesky 分解仅当矩阵
分解结构示例:
9.3 计算方法与示例
1. 计算推导 (以 3x3 矩阵为例)
我们希望找到
通过逐个对比矩阵两边的元素,我们可以按顺序求解
这是一个递归过程,计算每个
2. 数值示例
对以下对称正定矩阵
- 第一列:
- 第二列:
- 第三列:
最终得到 Cholesky 因子
验证:
9.4 Cholesky 分解算法 (General Algorithm)
对于一个
- 对角元素 (
): - 非对角元素 (
for ):
计算流程:
按列进行计算,从 j = 1 到 n:
- 首先使用对角元素公式计算
。 - 然后,对于该列下方的所有元素 (
i = j + 1到n),使用非对角元素公式计算。
9.5 在机器学习中的应用
Cholesky 分解是机器学习中高效数值计算的关键工具,尤其适用于处理协方差矩阵等对称正定矩阵。
- 从多元高斯分布中采样: 如果已知协方差矩阵
的 Cholesky 分解 ,我们可以通过 生成服从 的样本,其中 是一个标准正态分布的随机向量。 - 随机变量的线性变换: 该分解可以高效地实现随机变量的线性变换,这在深度随机模型(如变分自编码器 VAE)中被大量使用。
- 高效计算行列式: 由于
是三角矩阵,其行列式是主对角元素的乘积。因此, 。这比直接计算行列式要快得多且数值上更稳定。
10. 特征分解与对角化 (Eigendecomposition and Diagonalization)
特征分解是将一个矩阵分解为由其特征值和特征向量组成的矩阵的过程。如果一个矩阵可以被特征分解,它就可以被对角化 (Diagonalize),这极大地简化了与该矩阵相关的计算。
10.1 可对角化矩阵 (Diagonalizable Matrix)
对角矩阵 (Diagonal Matrix) 是所有非主对角线元素都为零的矩阵。它具有非常优良的计算性质:
- 行列式:
- 幂运算:
- 逆矩阵:
(如果所有 )
可对角化定义: 一个方阵
对角化
10.2 特征分解定理 (Eigendecomposition Theorem)
核心关系: 矩阵方程
设
因此,
定理 (特征分解/可对角化定理): 一个
当且仅当
此时,
是由这 个线性无关的特征向量构成的可逆矩阵。 是由对应的特征值构成的对角矩阵。
不可对角化的矩阵: 如果一个
10.3 谱定理 vs. 特征分解定理
| 特性 | 特征分解定理 (一般情况) | 谱定理 (特殊情况) |
|---|---|---|
| 适用对象 | 任何 |
仅限实对称矩阵 ( |
| 分解形式 | ||
| 分解条件 | 必须有 |
保证存在 |
| 特征值 | 可能是复数 | 保证是实数 |
| 特征向量矩阵 | ||
| 关系 | 谱定理是特征分解定理在一个更强、性质更好的特例。 | 每个实对称矩阵都可对角化,并且是正交可对角化。 |
10.4 对称矩阵的可对角化性
定理: 任何一个实对称矩阵
这是谱定理的直接推论。因为谱定理保证了:
- 实对称矩阵的所有特征值都是实数。
- 实对称矩阵总能找到
个线性无关的特征向量,这些特征向量甚至可以被构造成一个标准正交基。 - 因此,总能找到一个正交矩阵
(其列是标准正交的特征向量) 和一个对角矩阵 (其对角元是特征值),使得 。 - 由于
是正交的,我们有 ,所以分解也符合 的形式,证明了对称矩阵总是可对角化的。
10.5 特征分解的几何解释
特征分解
-
切换到特征基 (Change of Basis):
将输入向量 从标准坐标系转换到由 的特征向量构成的“特征坐标系” (eigenbasis) 中,得到新坐标 。
-
沿轴缩放 (Scaling):
- 在特征坐标系中,线性变换
的作用变得极其简单:它只是将新坐标 的每个分量(即沿着每个特征向量方向的分量)乘以对应的特征值 。这是一个纯粹的、沿坐标轴的拉伸或压缩。
- 在特征坐标系中,线性变换
-
切换回标准基 (Change back to Original Basis):
将经过缩放后的向量 从特征坐标系转换回标准坐标系,得到最终的变换结果 。
总结: 特征分解揭示了任何可对角化的线性变换的本质——它无非是在一个特定(特征向量)的坐标系下的**“切换基 → 缩放 → 切换回来”**三部曲。
10.6 非对称矩阵的特征分解示例
我们对一个非对称矩阵
考虑非对称矩阵:
第一步:计算特征值
求解特征方程
利用求根公式,得到特征值:
所以,
第二步:计算特征向量
对每一个特征值
-
对于
: 从第一行得到:
。
我们可以令,则对应的特征向量 。 -
对于
: 从第一行得到:
。
我们可以令,则对应的特征向量 。
第三步:构建 P 和 D 矩阵
将特征向量作为列向量构建矩阵
最终,矩阵
10.7 谱定理与对角化定理总结
| 特性 | 谱定理 (Spectral Theorem) | 对角化定理 (Diagonalization Theorem) |
|---|---|---|
| 适用矩阵 | 实对称矩阵 ( |
任何可对角化的方阵 |
| 可对角化性 | 总是可以对角化 | 不一定,仅当存在 |
| 特征值 | 保证为实数 | 可能是复数 |
| 特征向量 | 存在一组标准正交 (orthonormal) 的特征向量基 | 只需要线性无关 (linearly independent),不要求正交 |
| 分解形式 | ||
| 变换矩阵 |
核心区别总结:
- 谱定理(针对对称矩阵)给出了一个非常强的保证:不仅总是可以对角化,而且可以用一个结构优美的正交矩阵来实现。
- 对角化定理(针对一般方阵)的条件则更为宽泛:它只要求有足够的线性无关的特征向量,而不保证这些向量是正交的,甚至不保证矩阵一定能被对-角化。
11. 特征分解的应用
特征分解之所以重要,不仅因为它揭示了矩阵变换的内在几何结构,还因为它为许多复杂的矩阵运算提供了高效的计算途径。
11.1 矩阵的幂运算 (Matrix Powers)
直接计算一个矩阵的高次幂
由于矩阵乘法满足结合律,中间的
因此,我们得到:
这个公式的威力在于,计算对角矩阵的幂
结论: 计算
11.2 行列式计算 (Determinant Calculation)
我们也可以利用特征分解来高效计算行列式,并再次验证行列式与特征值的关系。
假设矩阵
而对角矩阵
这再次证明了一个矩阵的行列式等于其所有特征值的乘积。
12. 展望:奇异值分解 (Singular Value Decomposition, SVD)
特征分解是一个强大有力的工具,但它有一个根本性的限制:它只适用于方阵。
为了将矩阵分解的思想推广到任意形状的非方阵(例如
第六讲:奇异值分解 (SVD), 矩阵近似
12. 奇异值分解 (Singular Value Decomposition, SVD)
奇异值分解是线性代数中最重要、最普适的矩阵分解方法,有时被称为“线性代数基本定理”。它将特征分解的思想从方阵推广到了任意形状的矩阵。
12.1 SVD 定理
对于任何一个
其中:
( ): 一个正交矩阵。它的列向量 被称为左奇异向量 (left-singular vectors)。它们构成了输出空间 的一组标准正交基。 ( ): 一个正交矩阵。它的列向量 被称为右奇异向量 (right-singular vectors)。它们构成了输入空间 的一组标准正交基。 ( ): 一个伪对角矩阵 (pseudo-diagonal matrix),其形状与 相同。 - 它的“对角线”上(即
位置)的元素 是奇异值 (singular values)。 - 所有奇异值都是非负的 (
),并按降序排列: ,其余奇异值为0。 - 所有非对角线元素都为零。
- 它的“对角线”上(即
12.2 SVD 的几何直观解释
SVD 将一个线性变换
- 输入空间的基变换 (旋转/反射): 矩阵
作用于输入向量。由于 是正交矩阵,这对应于一次旋转或反射。它将输入空间的标准基对齐到一组新的、更“合适”的标准正交基(即右奇异向量 V的列)。 - 缩放与维度变换: 伪对角矩阵
沿着新的坐标轴对向量进行缩放(乘以对应的奇异值 ),并处理维度的变化(如果 ,会增加零维度;如果 ,会丢弃一些维度)。 - 输出空间的基变换 (旋转/反射): 矩阵
作用于变换后的向量。这对应于在输出空间中的一次旋转或反射,将经过缩放和维度变换后的向量对齐到最终的位置。
12.3 SVD 的构造方法
SVD 与特征分解密切相关。构造 SVD 的关键技巧是利用原矩阵
-
构造并分析
(求解 V 和 Σ): 是一个 的对称半正定矩阵。根据谱定理,它可以被正交对角化: 。 - 另一方面,如果我们假设 SVD 存在 (
),那么: 。 - 比较这两个表达式,我们得出结论:
- 右奇异向量
V就是的特征向量矩阵 P。 - 奇异值
σᵢ的平方等于的特征值 λᵢ,即或 。
- 右奇异向量
-
构造并分析
(求解 U): - 类似地,
是一个 的对称半正定矩阵。 - 通过与
的特征分解 比较,可以得出: - 左奇异向量
U就是的特征向量矩阵 S。
- 左奇异向量
- 类似地,
-
更高效的构造方法与奇异值方程:
- 在实践中,我们通常只计算一个(比如
)来得到 和 。 - 然后,利用奇异值方程 (Singular Value Equation) 来直接计算
的列向量: - 因此,对于所有非零奇异值
: - 这个方程也揭示了 SVD 的一个深刻联系:
将它的一个右奇异向量 映射为对应左奇异向量 的一个倍数,缩放因子就是奇异值 。
- 在实践中,我们通常只计算一个(比如
重要注记: 这种通过构造
13. 矩阵近似与SVD的应用
SVD 最强大的应用之一是低秩近似 (Low-Rank Approximation),它构成了现代数据压缩、降噪和推荐系统的数学基础。
13.1 SVD作为秩-1矩阵之和
任何一个秩为
: 第 对左、右奇异向量的外积 (outer product),形成一个秩-1矩阵。 : 对应的奇异值,作为这个秩-1矩阵的权重。
解释:
SVD 将一个复杂的矩阵分解成了若干个简单的、带有权重的“基本模式”的叠加。奇异值的大小代表了每个“基本模式”的重要性。
13.2 最佳低秩近似:Eckart-Young定理
如果我们不加总所有的
这个近似为什么好?Eckart-Young定理给出了答案。
- 谱范数: 我们需要一种衡量矩阵大小或近似误差的方法。谱范数
定义为矩阵 能将一个单位向量拉伸到的最大长度,它等于最大的奇异值 。 - 定理内容: 在所有秩为
的矩阵中,由SVD截断前 项得到的近似矩阵 是与原矩阵 最接近的一个(在谱范数和弗罗贝尼乌斯范数下)。 - 近似误差: 这个最佳近似的误差大小(用谱范数衡量)恰好等于被丢弃的第一个奇异值
。
意义:
- 最优性保证: SVD提供了一种构造最佳低秩近似的“配方”。
- 误差可控: 我们可以通过观察奇异值的大小来预估近似带来的误差。如果
很小,说明这个秩-k近似的质量非常高。 - 应用: 这正是SVD被广泛用于数据压缩、数据去噪和降维(如主成分分析PCA)的理论基础。
13.3 SVD的潜在结构解释能力
- SVD不仅仅是一个数学工具,它能够揭示数据中隐藏的模式。在“用户-电影”评分矩阵这类应用中:
- 左奇异向量
U的列: 可被解释为物品的**“主题”或“类型”**。 - 右奇异向量
V的列: 可被解释为用户的**“原型”或“偏好群组”**。 - 奇异值
Σ的对角元: 代表了每个“主题-原型”模式的强度。
- 左奇异向量
- 通过保留少数几个最大的奇异值,SVD能够提取出数据中最主要的、潜在的结构,从而使数据变得可解释,并能够用于预测和推荐。
第七讲:向量微积分 (Vector Calculus)
讲座主题: 单变量函数微分,偏微分与梯度,向量值函数的梯度,矩阵的梯度,梯度计算实用恒等式
第一部分:从单变量到多变量微积分
本讲座将从最基础的微积分概念开始,逐步推广到处理向量和矩阵的多元微积分,这对于理解和实现机器学习中的优化算法至_关重要。
1. 核心概念回顾
1.1 函数 (Functions)
- 核心: 函数是建立输入与输出之间关系的核心数学工具。
- 定义: 一个函数
将一个输入 (input) 映射到一个输出 (target) 。 - 记法:
,其中 。
1.2 梯度在机器学习中的作用
- 重要性: 梯度指明了函数值上升最快的方向 (direction of steepest ascent)。在优化算法中,我们沿着梯度的反方向移动,以找到函数的最小值点。
2. 单变量函数的微分 (Differentiation of Univariate Functions)
本节回顾了单变量微积分的基础。
-
差商 (Difference Quotient):
差商计算的是函数图像上两点之间割线的斜率,代表了区间的平均变化率。
-
导数 (Derivative):
当(或记为 ) 趋近于 0 时,割线逼近切线。这条切线的斜率就是函数 在点 的导数。 导数代表了函数在该点的瞬时变化率。
3. 泰勒级数 (Taylor Series)
泰勒级数是微积分中一个极其强大的工具,它允许我们将一个复杂的、可微的函数用一个无穷多项式来表示,从而在局部近似和分析函数的行为。
3.1 泰勒多项式 (Taylor Polynomial)
- 定义: 函数
在点 处的 n 阶泰勒多项式 是泰勒级数的有限项截断,它提供了对原函数的一个局部近似。其定义为: 其中 是函数 在点 的 k 阶导数。 - 近似的意义: 阶数
n越高,泰勒多项式在附近就越能精确地模拟原函数 的行为。
3.2 泰勒级数与麦克劳林级数
- 泰勒级数: 当 n 趋近于无穷时,泰勒多项式就变成了泰勒级数。这要求函数是无限次可微的 (
)。 - 麦克劳林级数 (Maclaurin Series) 是泰勒级数的一个重要特例,即在展开点
处展开。
3.3 泰勒级数与幂级数的关系
- 幂级数 (Power Series) 是任何形如
的无穷级数。 - 泰勒级数是幂级数的一个特例,其特殊之处在于,系数
不是任意的,而是由函数 在展开点 的各阶导数唯一确定的:
第二部分:多元函数的微分
现在,我们将微积分的思想从单变量函数推广到处理多个变量的函数,这是向量微积分的核心。
4. 偏导数与梯度
4.1 偏导数 (Partial Derivative)
- 核心思想: 计算多变量函数对其中一个变量的变化率,同时将所有其他变量视为常数。
- 定义:
4.2 梯度 (Gradient)
- 定义: 一个多元标量值函数
的梯度,是将其对每一个自变量的偏导数收集到一个行向量中。 - 记法与符号约定: 在本课程的语境下,以下符号是等价的,都代表梯度:
- 维度: 如果
(列向量),其梯度是 的行向量。 - 几何意义: 梯度向量指向函数值上升最快的方向。
5. 雅可比矩阵与多元链式法则
5.1 雅可比矩阵 (Jacobian Matrix)
- 推广: 当我们的函数是一个向量值函数,即
时,我们需要一个矩阵来包含所有的导数信息。 - 定义: 函数
的雅可比矩阵 是一个 的矩阵,其第 i行是输出向量的第i个分量的梯度。 - 梯度是雅可比矩阵的特例: 当函数是标量值时 (
),其 的雅可比矩阵就是我们之前定义的梯度(行向量)。
5.2 多元链式法则 (Chain Rule for Multivariate Functions)
- 核心法则: 链式法则是计算复合函数导数的基础。它的通用形式是雅可比矩阵的乘积。
- 形式: 对于复合函数
,其导数为: - 解读: 这是一个矩阵乘法。如果
且 ,那么最终结果 是一个 的雅可比矩阵。 - 通用性: 这个法则适用于任意层数的函数复合,例如
的导数是 。
5.3 核心求导示例
-
示例1: 线性变换的雅可比
- 问题: 计算函数
对 的导数(雅可比矩阵),其中 。 - 推导:
- 函数的第
i个分量是。 - 计算其对
的偏导数: 。 - 将这些偏导数
填入雅可比矩阵:
- 函数的第
- 结论:
- 问题: 计算函数
-
示例2:最小二乘损失的梯度
- 问题: 计算损失函数
对参数 的梯度 。 - 重要性: 这是线性回归等模型的核心优化问题。
- 步骤 (使用链式法则):
- 设误差
,则 。 - 应用链式法则:
。 - 计算各部分:
(这是一个 的梯度), (这是一个 的雅可比矩阵)。 - 组合结果:
- 设误差
- 问题: 计算损失函数
6. 矩阵的梯度 (Gradients of/with respect to Matrices)
6.1 概念与挑战
- 张量结构: 当我们对矩阵求导时,例如计算
矩阵 对 矩阵 的导数,结果是一个复杂的四维张量。其第 (i,j,k,l)个元素是。 - 实践中的简化: 在实践中,直接处理高维张量很不方便。一个常用的技巧是将矩阵“展平”(flatten) 为向量,然后问题就退化为我们熟悉的向量对向量求导,其结果是一个大的雅可比矩阵。
6.2 核心示例推导
-
示例1: 向量函数对矩阵的梯度
- 问题: 对于
,计算 。 - 推导:
- 输出的第
i个分量。 - 计算
对 的偏导数: - 这个结果表明,输出
只依赖于矩阵 的第 i 行 。 - 对该行求导的结果是:
- 输出的第
- 结论 (雅可比矩阵结构): 对整个输出向量
求导时,其对 的梯度是一个块状结构的雅可比矩阵。例如,对 的导数部分,其结构是一个在第 i个块位置上为的大行向量:
- 问题: 对于
-
示例2: 矩阵函数对矩阵的梯度
- 问题: 对于
,计算 。 - 推导:
- 输出矩阵的元素
。 - 计算其对
的偏导数: 。 - 这个结果表明,输出矩阵
的第 i行只依赖于输入矩阵 的第 i 行 。
- 输出矩阵的元素
- 结论 (块状雅可比):
- 对
的第 i行求导,我们得到一个矩阵: - 对整个输出
求导时,其雅可比矩阵也呈块状结构。例如,对输出的第 i行求导,其结果为:
- 对
- 问题: 对于
第三部分:矩阵微积分实用恒等式与证明
直接通过定义计算矩阵和向量的梯度通常非常繁琐。在实践中,我们更多地是依赖于一些已经证明的、可以直接套用的求导恒等式。本节将介绍一些在机器学习和优化中最重要的恒等式。
7. 核心求导恒等式
在下面的公式中,我们假设变量 X 是一个矩阵,x, a, b 是向量。
7.1 涉及转置、迹和行列式的恒等式
-
转置的导数:
- 解读: 对一个矩阵值函数的转置求导,等于先求导再对结果(通常是一个高维张量)进行相应的“转置”操作。
-
迹的导数 (Trace Trick):
- 解读: 迹
tr(·)算子和求导∂/∂X算子可以交换顺序。这个技巧在推导复杂标量损失函数对矩阵的梯度时极其有用。
- 解读: 迹
-
行列式的导数:
- 解读: 行列式的导数与原行列式、原函数的逆以及原函数的导数有关。这个公式也被称为雅可比公式 (Jacobi's Formula)。
7.2 涉及逆矩阵和双线性/二次型的恒等式
-
逆矩阵的导数:
- 类比: 这与标量求导
d/dx(1/f) = -f'/f²非常相似,但由于矩阵乘法不可交换,顺序非常重要。
- 类比: 这与标量求导
-
线性形式的梯度:
- 证明:
。对 xₖ求偏导∂f/∂xₖ = aₖ。将所有偏导数aₖ组成行向量,即得到aᵀ。
- 证明:
-
双线性形式 (Bilinear Form) 的梯度:
- 证明:
f(X) = Σᵢ Σⱼ aᵢ Xᵢⱼ bⱼ。对Xₖₗ求偏导,只有当i=k且j=l时项不为零,结果为aₖbₗ。将所有偏导数组成矩阵,即得到外积abᵀ。
- 证明:
-
二次型 (Quadratic Form) 的梯度:
- 证明:
。对 xₖ求偏导,需要使用乘法法则,最终会得到两项。一项来自xᵢ(当i=k),另一项来自xⱼ(当j=k)。整理后得到[Bx]ₖ + [Bᵀx]ₖ,即(B+Bᵀ)x的第 k 项。将其写成行向量形式即为xᵀ(B+Bᵀ)。 - 重要特例: 如果矩阵
是对称的 ( ),则梯度简化为: 这与标量求导 d/dx(bx²) = 2bx的形式非常相似。
- 证明:
-
加权最小二乘的梯度:
- 前提:
是一个对称矩阵。 - 解读: 这是二次型梯度公式的一个直接应用,通过链式法则推导得出。它是解决加权最小二乘问题的关键。
- 前提:
-
逐元素函数 (Element-wise Function) 的雅可比:
- 设
g(·)是一个作用于标量的函数,当我们将其逐元素应用于向量时,得到向量函数 。 - 其雅可比矩阵是一个对角矩阵:
- 示例:
- 设
这些恒等式构成了矩阵微积分的“公式表”,在推导机器学习算法的梯度时,可以直接引用,从而避免了繁琐的逐元素求导。
8. 核心求导恒等式与证明
8.1 线性形式的梯度 (Gradient of a Linear Form)
- 恒等式:
- 证明:
- 设
。由于点积满足交换律, 。我们展开这个标量函数: - 我们来计算梯度,即对
的每一个分量 求偏导数: - 在这个求和中,只有当
时,项 才与 有关。所有其他项(当 时)对于求导来说都是常数,其导数为0。 - 因此,偏导数简化为:
- 将所有这些偏导数
aₖ组合成一个行向量,就得到了梯度: - 证毕。
- 设
8.2 双线性形式的梯度 (Gradient of a Bilinear Form)
- 恒等式:
- 证明:
- 设
,其中 。这是一个标量函数。我们将其展开: - 我们要计算
对矩阵 中任意一个元素 的偏导数。 - 在这个双重求和中,只有当求和的下标
i和j同时等于我们求导的下标k和l时(即i=k且j=l),这一项才与变量有关。 - 因此,所有其他项的偏导数都为0,只剩下一项:
- 这个结果
aₖbₗ正是矩阵外积在第 k行第l列的元素。 - 由于这对所有
k和l都成立,所以整个梯度矩阵就是: - 证毕。
- 设
8.3 二次型的梯度 (Gradient of a Quadratic Form)
- 恒等式:
- 证明:
- 设
,其中 。我们将其展开: - 我们计算
对向量 的任意一个分量 的偏导数。这里需要使用乘法法则,因为 可能以 或 的形式出现。 - 利用克罗内克-德尔塔符号
(当 时为1,否则为0),我们有 。应用乘法法则: - 将其代回求和式:
这个双重求和可以拆成两部分: - 在第一部分,由于
的存在,只有当 时项不为零,所以它简化为 。这正是矩阵-向量乘积 的第 k个元素。 - 在第二部分,由于
的存在,只有当 时项不为零,所以它简化为 。这可以看作是 x与B的第 k 列的点积,也等于矩阵-向量乘积的第 k个元素。 - 因此,我们得到:
- 将所有这些偏导数
(B+Bᵀ)x的分量组合成一个行向量,就得到了梯度: - 证毕。
- 设
- 重要特例: 如果矩阵
是对称的 ( ),那么 ,梯度简化为:
第八讲:反向传播与自动微分,高阶导数,线性化与多元泰勒级数,使用梯度下降进行优化
第一部分:反向传播与自动微分 (Backpropagation and Automatic Differentiation)
在机器学习中,我们通过优化算法(如梯度下降)来调整模型参数,而这些算法的核心就是计算目标函数(损失函数)相对于模型参数的梯度。对于深度神经网络这样复杂的复合函数,如何高效、准确地计算梯度,是一个至关重要的问题。
1. 梯度计算的挑战
- 链式法则 (Chain Rule):
链式法则是计算复合函数梯度的数学基础。对于,其导数为: - 问题: 对于深度神经网络这种由许多层函数嵌套而成的复杂模型,如果直接、显式地写出梯度的解析表达式,这个表达式会变得极其冗长和复杂,难以手动推导和实现,并且计算成本可能远高于计算函数本身。
2. 解决方案:反向传播与自动微分
为了解决这个挑战,我们不直接求解最终的梯度表达式,而是采用更智能的算法。
-
反向传播 (Backpropagation):
- 这是一个专门为神经网络设计的、高效计算梯度的算法。
- 它的核心思想是利用链式法则,从网络的输出层开始,逐层向后计算梯度,并将计算出的梯度“传播”回前一层,从而避免了大量的重复计算。
-
自动微分 (Automatic Differentiation, AD):
- 这是一个更广义的计算概念。它是一套能够对由计算机程序定义的函数计算出精确导数的技术。
- AD 不是符号微分(像 WolframAlpha 那样推导公式),也不是数值微分(用差商近似),而是通过追踪程序中的每一个基本运算(加、减、乘、除、sin、exp等),并系统地应用链式法则,来得到精确的梯度值。
- 优点: 精确、高效,并且能够很好地扩展到高维问题。
-
两者的关系:
- 反向传播是自动微分的一种特殊形式,即“反向模式自动微分 (Reverse-mode AD)”。
- 可以说,反向传播是自动微分在深度学习领域的成功应用和具体实现。
- 这些技术使得基于梯度的优化方法在现代大规模机器学习模型中变得可行。
3. 深度网络中的梯度计算
- 深度网络的结构: 一个深度学习网络的输出可以看作是一个由 K 层函数复合而成的结果:
其中 是输入, 是输出。 - 每层的计算: 每一层
的计算通常包含一个线性变换和一个非线性激活函数 : 其中 是前一层的输出, 和 是这一层的权重和偏置参数。 - 递归定义: 整个网络的计算可以被看作一个递归过程:
(第0层是输入) , for
在这个层层嵌套的结构中,计算最终损失函数相对于任何一层参数(如
4. 反向传播的核心思想:逐层计算与梯度复用
4.1 训练目标与梯度
- 目标: 训练一个深度网络,就是找到一组最优的参数
,使得损失函数 (例如,均方误差 )最小化。 - 方法: 使用基于梯度的优化算法。这要求我们计算出损失
相对于所有参数的梯度。 - 策略: 我们不把所有参数看作一个巨大的向量来求梯度,而是逐层 (layer by layer) 分别计算损失
相对于每一层参数 的偏导数 。最后,将所有这些逐层梯度拼接起来,就得到了完整的总梯度 ,用于更新参数。
4.2 链式法则的系统性应用
下图展示了如何利用链式法则来系统性地计算每一层的梯度。
-
符号说明:
: 第 i层的输出向量。: 第 i层的参数。
-
梯度计算链条:
要计算损失相对于第 i层参数的梯度 ,我们需要将从最终损失 到 的所有“影响”路径串联起来: : 损失函数对网络最终输出的梯度。这是计算的起点。 : 第 j+1层的输出对第j层输出的梯度。这描述了层与层之间的梯度传播。: 第 i层的输出对其自身参数的梯度。这是我们最终需要的**“本地”梯度**。
4.3 反向传播的精髓:梯度复用
观察上面的梯度计算链条,我们可以发现一个极其重要的模式。
-
计算
: -
计算前一层
:
关键洞察:
计算
这个括号里的部分,其实就是损失 i 层输出
算法流程 (反向传播):
- 从最后一层开始: 计算
。 - 计算最后一层的参数梯度:
。 - 向后传播梯度: 计算损失相对于倒数第二层输出的梯度:
- 计算倒数第二层的参数梯度:
。 - 重复: 不断地将“上游梯度”
向后乘以一个“本地雅可比矩阵” ,得到新的“上游梯度” ,然后用它来计算当前层的参数梯度。
结论:
反向传播算法的本质就是高效地复用中间计算结果。通过从后向前逐层计算和传递“误差信号”(即损失对各层输出的梯度),它避免了为每个参数从头开始计算整个链式法则的巨大冗余,从而使得训练深度神经网络在计算上成为可能。
5. 自动微分 (Automatic Differentiation, AD)
自动微分是一套更通用、更底层的技术,而反向传播是它在神经网络中的一种具体实现。
5.1 什么是自动微分?
- 定义: 自动微分 (AD) 是一系列技术,它能够通过系统性地将链式法则应用于构成一个函数的基本运算(如加、减、乘、除、
sin,exp等),来计算出该函数(通常由计算机程序定义)的精确导数(在机器精度内)。 - 核心思想: 任何复杂的函数计算过程,都可以被分解为一系列简单的、可微的基本操作。AD 通过追踪这些操作,并自动应用链式法则,来得到最终的梯度。
- 与反向传播的关系: 反向传播是反向模式自动微分 (Reverse-mode AD) 的一个特例,它专门用于计算神经网络中标量值损失函数相对于所有参数的梯度。
5.2 计算图 (Computational Graph)
为了系统性地应用链式法则,AD 将一个函数的计算过程表示为一个有向无环图 (DAG),即计算图。
- 结构:
- 节点 (Nodes): 代表变量(输入、中间变量、输出)。
- 边 (Edges): 代表基本操作或函数。
- 链式法则在计算图上的体现:
- 对于一个函数
,其计算图可以看作是 x -> a -> b -> y。 - 计算总梯度
,就需要将从输出到输入路径上的所有“本地梯度”相乘:
- 对于一个函数
- 中间变量的作用:
- 将一个复杂的函数(如幻灯片中的例子)分解为一系列简单的中间变量,例如
a=x²,b=exp(a),c=a+b... - 这样做不仅在计算函数值时可以复用结果、提高效率,更重要的是,它为应用链式法则、高效计算梯度提供了清晰的路径和结构。
- 现代深度学习框架(如 PyTorch, TensorFlow)的核心就是构建和操作这样的计算图。
- 将一个复杂的函数(如幻灯片中的例子)分解为一系列简单的中间变量,例如
5.3 自动微分的两种模式:前向模式 vs. 反向模式
AD 主要有两种不同的计算策略,它们的区别在于应用链式法则的顺序。
-
前向模式 (Forward Mode / Forward Accumulation):
- 方向: 与数据流动的方向相同,即从输入到输出 (从左到右) 计算梯度。
- 过程 (对于
y=b(a(x))):- 先计算
。 - 然后计算
,并与上一步结果相乘,得到 。 - 最后计算
,并与上一步结果相乘,得到最终的 。
- 先计算
- 适用场景: 当输入维度
n远小于输出维度m(n ≪ m) 时非常高效。例如,计算一个函数的雅可比矩阵与某个特定方向向量的乘积 (Jacobian-vector product)。
-
反向模式 (Reverse Mode / Backpropagation):
- 方向: 与数据流动的方向相反,即从输出到输入 (从右到左) 计算梯度。
- 过程 (对于
y=b(a(x))):- 前向传播: 首先,需要执行一次完整的前向计算(从
x到y),并存储所有中间变量的值。 - 反向传播:
- 从最终输出开始,计算
。 - 然后向后一步,计算
。 - 最后计算
。
- 从最终输出开始,计算
- 前向传播: 首先,需要执行一次完整的前向计算(从
- 适用场景: 当输出维度
m远小于输入维度n(m ≪ n) 时极其高效。 - 这完美地匹配了神经网络的训练场景:输入(参数
θ)的维度可能有数百万甚至上亿,而输出(损失函数L)是一个标量(维度为1)。
结论:
反向模式自动微分(即反向传播)是深度学习能够成功训练拥有海量参数的模型的计算基石。它使得我们能够以仅仅比一次前向传播多一点的计算成本,高效地计算出损失函数相对于所有参数的精确梯度。
6. 反向传播的具体流程:在计算图上应用链式法则
6.1 步骤一:前向传播与局部导数计算
在反向传播开始之前,我们需要完成两件事:
-
前向传播 (Forward Pass): 从输入
x开始,按照计算图的顺序,一步步计算出所有的中间变量 (a, b, c, ...),直到最终的输出f。在这个过程中,所有中间变量的值都必须被存储下来,因为它们在反向传播时会被用到。 -
计算局部导数 (Local Derivatives): 对于计算图中的每一个节点(或说每一个基本运算),我们都可以直接计算出其输出相对于其直接输入的导数。这些被称为“局部导数”。
- 例如,对于
a = x²,局部导数是∂a/∂x = 2x。 - 对于
c = a + b,局部导数是∂c/∂a = 1和∂c/∂b = 1。 - 这些局部导数非常简单,它们的计算公式是预先知道的。
- 例如,对于
6.2 步骤二:反向传播梯度
这是反向传播算法的核心。我们从最终的输出 f 开始,从后向前地计算损失(或最终输出)相对于每一个中间变量和输入的梯度。
-
起点: 最终输出
f相对于自身的梯度是 1,即∂f/∂f = 1。 -
传播规则 (多元链式法则):
要计算f相对于某个中间变量(例如c)的梯度∂f/∂c,我们需要找到所有从c指向最终输出f的路径,然后将所有路径上的梯度贡献加起来。∂f/∂c受到了所有“下游”节点(即所有以c作为输入的节点,如d和e)的影响。- 因此,
∂f/∂c等于它对所有子节点的贡献之和: - 这个公式可以被解读为:
f对c的总梯度 = (f对d的梯度 ×d对c的局部梯度) + (f对e的梯度 ×e对c的局部梯度)。
-
迭代计算:
我们从∂f/∂f = 1开始,利用这个规则,像剥洋葱一样,一层层地向后计算:
在每一步,我们都复用了上一步已经计算出的“上游梯度”(如 ∂f/∂c),这正是其高效的原因。
6.3 自动微分的形式化表述
我们可以将这个过程更形式化地描述。
- 计算图: 任何一个计算过程都可以表示为一系列基本函数的组合。输入为
,中间变量为 ,最终输出为 。每个中间变量 都是由其父节点 (parent nodes) 通过一个基本函数 计算得出的: - 反向模式梯度传播规则:
- 初始化:
。 - 对于任何一个变量
(从 向下到 ),其梯度为: - 解读: 一个节点的梯度,等于所有以它为输入的子节点 (children nodes) 的梯度,分别乘以对应的局部导数,然后求和。
- 初始化:
7. 自动微分的计算复杂度
- 惊人的效率: 尽管梯度的最终数学表达式可能看起来比原函数复杂得多,但自动微分(特别是反向模式)的计算复杂度与计算原函数本身的复杂度是同个数量级的。
- 原因: AD 通过将导数计算也视为计算图上的一个变量传递过程,复用了大量的中间结果。它计算梯度所需的运算次数,通常只是计算原函数所需运算次数的一个小的常数倍。
- 结论: 这种高效性是自动微分和反向传播能够成为训练大规模、复杂机器学习模型(如深度神经网络)的实用技术的关键原因。
第二部分:高阶导数与海森矩阵 (Higher-Order Derivatives and Hessian Matrix)
在掌握了一阶导数(梯度)之后,我们自然地会想:二阶导数在多元函数中是什么样的?它又有什么用?这就引出了海森矩阵的概念。
7. 高阶偏导数 (Higher-Order Partial Derivatives)
- 概念: 就像单变量函数可以求二阶、三阶甚至更高阶的导数一样,我们也可以对多元函数反复进行偏微分。
- 记法:
: 对函数 连续两次对变量 x求偏导。: 混合偏导数 (Mixed Partial Derivative)。表示先对 x求偏导,然后再对y求偏导。: 先对 y求偏导,然后再对x求偏导。
8. 海森矩阵 (Hessian Matrix)
8.1 定义
- 核心思想: 梯度是将所有一阶偏导数收集到一个向量中。类似地,海森矩阵就是将一个多元函数的所有二阶偏导数收集到一个矩阵中。
- 定义: 对于一个函数
,其海森矩阵 是一个 的方阵,其第 i行第j列的元素是混合偏导数。 - 记法: 海森矩阵通常记为
或 。 - 示例 (对于
):
8.2 对称性:克莱罗定理 (Clairaut's Theorem)
- 定理 (混合偏导的对称性): 如果一个函数
的所有二阶偏导数都是连续的(这在机器学习中我们遇到的函数通常都满足),那么求导的顺序无关紧要。 - 重要推论: 这个定理直接导致了海森矩阵是一个对称矩阵 (
)。对称矩阵具有许多优良的性质(如所有特征值为实数,可以被正交对角化),这使得对海森矩阵的分析变得更加方便。
8.3 海森矩阵的重要性与几何意义
-
几何意义: 如果说梯度(一阶导数)描述了函数曲面的局部倾斜度 (local slope),那么海森矩阵(二阶导数)则描述了函数曲面的局部曲率 (local curvature)。它告诉我们这个曲面在某一点附近是“向上弯曲”还是“向下弯曲”,以及在不同方向上弯曲的程度。
-
在优化中的核心作用:判断临界点类型
在优化过程中,当梯度时,我们到达了一个临界点 (critical point)。这个点可能是局部最小值、局部最大值,也可能是一个鞍点。海森矩阵的性质可以帮助我们准确地判断这一点: - 局部最小值 (Local Minimum): 如果在临界点处,海森矩阵
是正定的 (positive definite)(即所有特征值都为正),那么这个点是一个局部最小值。函数的形状像一个向上开口的“碗”。 - 局部最大值 (Local Maximum): 如果在临界点处,海森矩阵
是负定的 (negative definite)(即所有特征值都为负),那么这个点是一个局部最大值。函数的形状像一个向下开口的“帽子”。 - 鞍点 (Saddle Point): 如果在临界点处,海森矩阵
是不定的 (indefinite)(即既有正特征值也有负特征值),那么这个点是一个鞍点。函数在某些方向上向上弯曲,在另一些方向上向下弯曲,像一个马鞍。
- 局部最小值 (Local Minimum): 如果在临界点处,海森矩阵
用二阶导的优化方法 (The optimization method using the second-order derivative)
海森矩阵为我们提供了超越梯度的“二阶信息”,使我们能够更深入地分析损失函数的几何形状,并设计出更强大的优化算法(如牛顿法)。
第三部分:线性化与多元泰勒级数 (Linearization and Multivariate Taylor Series)
在理解了梯度和海森矩阵之后,我们可以将单变量的泰勒级数思想推广到多变量函数,这为理解和设计更高级的优化算法(如牛顿法)提供了理论基础。
9. 函数的线性化近似 (Linearization)
-
核心思想: 在任意一点
的附近,任何一个复杂但平滑的多元函数 ,都可以用一个简单的线性函数(在几何上是一个平面或超平面)来进行局部近似。 -
公式: 这个线性近似由函数在该点的值和梯度共同决定:
其中:
: 是近似的基准值(平面在 处的高度)。 : 是函数在 处的梯度(一个行向量),它定义了近似平面的“倾斜方向和陡峭程度”。 : 是从展开点 到目标点 的位移向量。 ·在这里代表向量的点积。
-
与泰勒级数的关系: 这个线性近似公式,正是多元泰勒级数的一阶截断。它只用到了函数的一阶导数信息。
-
局限性: 线性近似只在
的一个很小的邻域内是准确的。离 越远,近似的误差就越大。为了得到更精确的近似,我们需要引入更高阶的项。
10. 多元泰勒级数 (Multivariate Taylor Series)
10.1 定义
- 目标: 将单变量泰勒级数
推广到多元函数 。 - 定义: 设函数
在点 附近是平滑的(即高阶混合偏导连续且对称),并定义位移向量 。 在 处的多元泰勒级数可以紧凑地写为: 这个公式看起来很抽象,其中的关键是理解 和 的含义。
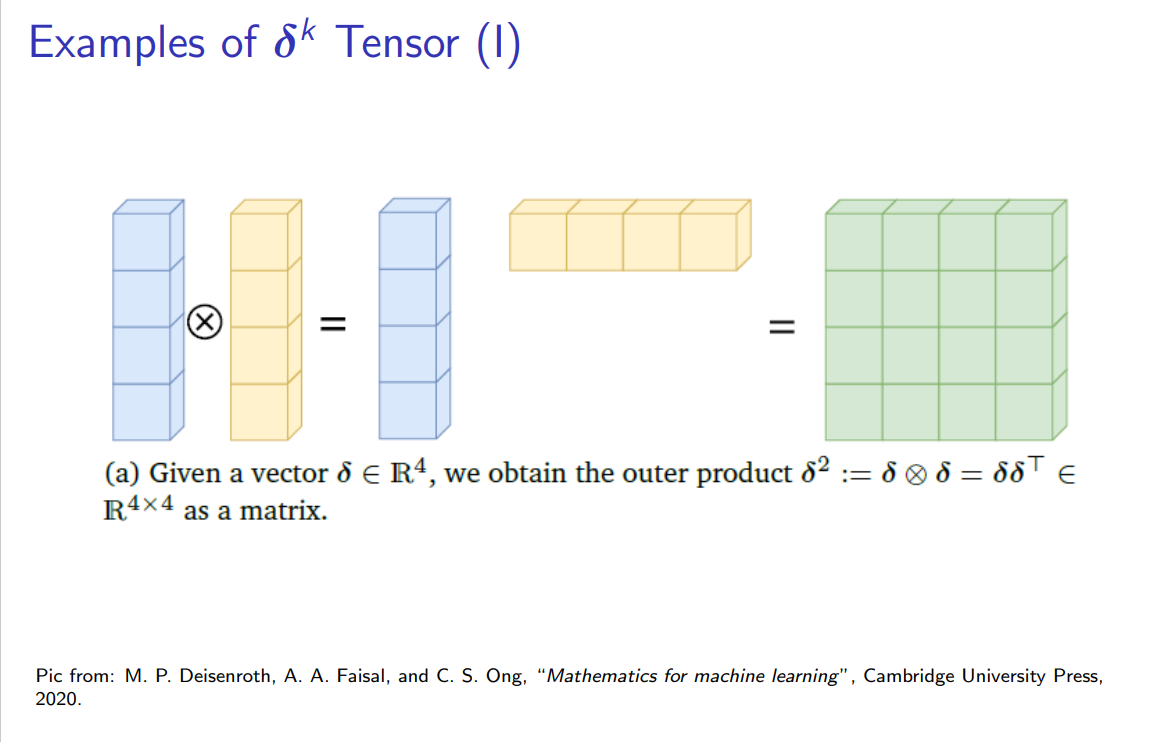
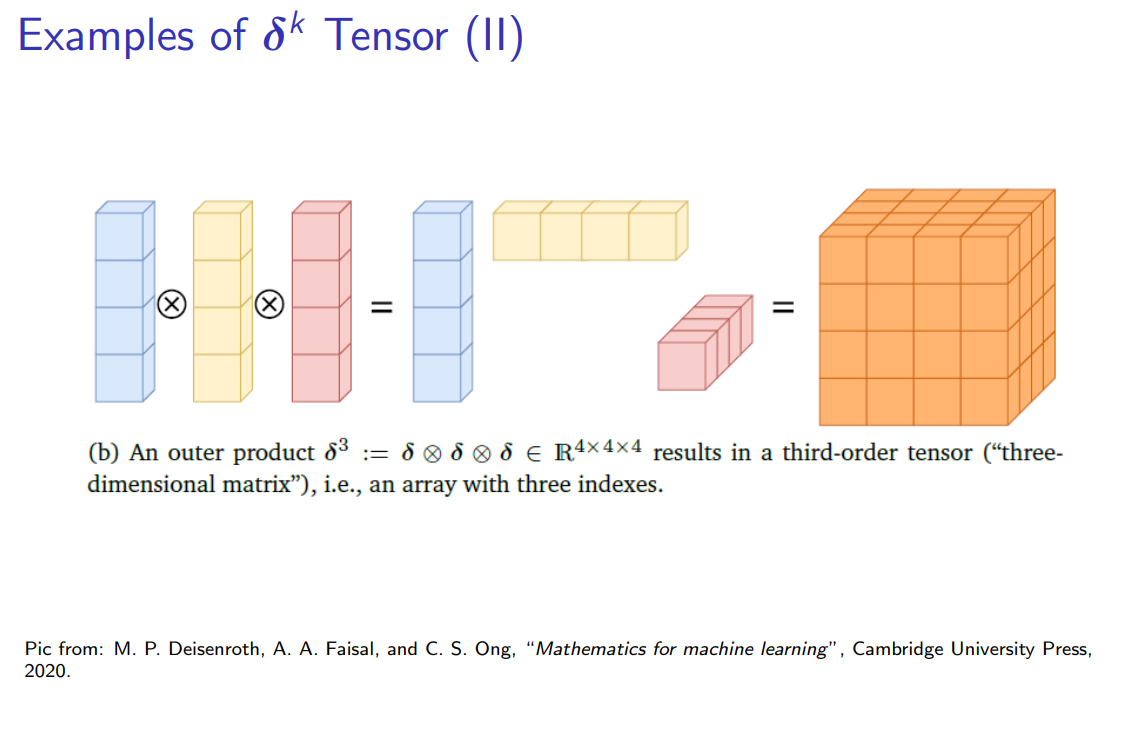
10.2 高阶导数张量
- k = 0:
(函数值本身,一个0阶张量,即标量)。 - k = 1:
(梯度,一个1阶张量,即向量)。 - k = 2:
(海森矩阵,一个2阶张量,即矩阵)。 - k = 3:
是一个 的三阶张量,其元素是所有可能的三阶偏导数,如 。
10.3 展开前几项
虽然通项公式使用了抽象的张量表示,但在实际应用中,我们通常只关心到二阶的展开。让我们把前几项写出来,以便更好地理解:
-
零阶项 (k=0):
-
一阶项 (k=1):
这正是我们前面提到的线性近似。
-
二阶项 (k=2):
这是一个二次型 (quadratic form)。它引入了关于函数曲率的信息。
10.4 二阶泰勒展开
将这些项组合起来,我们就得到了在优化中最常用、最重要的二阶多元泰勒展开:
这个公式用一个二次函数来近似原函数
第四部分:使用梯度下降进行优化 (Optimization Using Gradient Descent)
现在,我们将利用前面建立的微积分工具,特别是梯度和泰勒展开,来正式探讨机器学习中最核心的优化过程。
11. 优化的基本思想
- 目标: 对于一个给定的函数
(例如,机器学习中的损失函数),我们的目标是找到一组参数 ,使得 达到其(局部或全局)最小值。 - 迭代方法: 我们通常从一个随机的初始点
开始,然后通过一系列迭代步骤,逐步走向更好的参数点: 这里的关键在于如何确定每一步的更新方向和大小 。
12. 梯度下降法 (Gradient Descent)
梯度下降法是回答“如何确定更新方向”这个问题的最基本、最重要的方法。
12.1 核心思想:最速下降
- 回顾梯度: 梯度
指向了函数值上升最快的方向。 - 最速下降方向: 因此,梯度的反方向
就是函数值下降最快的方向。 - 算法: 梯度下降法的策略非常直观:在当前位置,计算出最陡峭的下山方向,然后沿着这个方向迈出一小步。
12.2 更新规则
梯度下降的迭代更新规则如下:
其中:
: 当前的参数位置。 : 在当前位置计算出的梯度向量。 : 学习率 (Learning Rate),是一个正的标量超参数。它控制了我们每一步“下山”的步子迈多大。
12.3 学习率
学习率的选择对优化过程至关重要:
- 学习率过小:
- 优点: 更新过程稳定,不太可能错过最小值点。
- 缺点: 收敛速度非常慢,需要大量的迭代次数才能到达谷底。
- 学习率过大:
- 优点: 开始时下降速度可能很快。
- 缺点: 可能会“跨过”最小值点,导致在谷底附近剧烈震荡,无法收敛,甚至可能导致损失值不降反升,使得优化过程发散。
12.4 梯度下降的几何解释:线性近似
梯度下降的更新规则,可以从对损失函数的一阶泰勒展开(线性近似)来理解。在
为了让
因此,选择更新方向为
13. 多元泰勒级数 (Multivariate Taylor Series)
13.1 定义
- 目标: 将单变量泰勒级数
推广到多元函数 。 - 定义: 设函数
在点 附近是平滑的(即高阶混合偏导连续且对称),并定义位移向量 。 在 处的多元泰勒级数可以紧凑地写为: (注:这里的 [...]不是矩阵,而是一种表示张量缩并的抽象记法)
这个公式看起来很抽象,其中的关键是理解
13.2 高阶导数张量
- 递归定义: 高阶导数可以看作是对前一阶导数(梯度、海森矩阵等)再求一次梯度。
- 一阶 (梯度):
- 二阶 (海森矩阵):
- 三阶:
- 一阶 (梯度):
- 核心规则: 每对一个导数对象(向量、矩阵、张量)再求一次梯度,就会为该对象增加一个新的维度。
- 一般形式: 对于一个输入为
维向量的函数,它的 k 阶导数是一个维度为 的 k 阶张量。 - 该张量在位置
上的元素是:
- 该张量在位置
导数阶数与对象类型的关系总结:
| 阶数 (Order) | 导数对象 (Object) | 形状 (Shape) | 几何/物理意义 |
|---|---|---|---|
| 1st | 梯度 (Gradient) | 向量 (n) | 局部最陡峭的斜坡 |
| 2nd | 海森矩阵 (Hessian) | 矩阵 ( |
局部斜坡的变化率 (曲率) |
| 3rd | 三阶导数张量 | 三阶张量 ( |
局部曲率的变化率 |
13.3 位移向量的张量幂
在单变量泰勒级数中,我们有
- k = 1:
(位移向量本身)。 - k = 2:
(向量的外积,一个 的矩阵)。 - k = 3:
是一个 的三阶张量。 - 一般情况:
是一个 k 阶张量,其在位置 上的元素是:
13.4 展开前几项 (将张量运算具体化)
现在我们可以理解多元泰勒级数中每一项的真正含义了。每一项都是一个 k 阶导数张量和一个 k 阶位移张量的缩并 (Contraction),结果是一个标量。
- 零阶项 (k=0):
- 一阶项 (k=1):
是一个 的行向量 (梯度)。 是一个 的列向量。 - 它们的缩并就是点积:
- 二阶项 (k=2):
是一个 的矩阵 (海森矩阵 )。 是一个 的矩阵 ( )。 - 它们的缩并是一种双点积 (double dot product),在矩阵形式下可以方便地写成二次型:
- 三阶项 (k = 3):
- 最终的二阶泰勒展开:
将这些项组合起来,我们就得到了在优化中最常用、最重要的二阶多元泰勒展开:这个公式用一个二次函数来近似原函数 在 附近的形状,是牛顿法等二阶优化算法的理论基础。
13.5 完整展开 (Full Series to Order n)
- 表达:
-
- 余项:
可用 Lagrange 或积分形式表示。 - Lagrange 余项:
- 收敛条件: 当
时 ,级数收敛。
第五部分:连续优化 (Continuous Optimization)
在机器学习中,“训练模型”的本质通常是一个连续优化问题。我们试图找到一组连续变化的参数,使得某个衡量模型好坏的指标(损失函数)达到最优。
14. 优化的基本框架
- 目标: 找到一组“好”的模型参数
。 - “好”的定义: “好”的参数能够使目标函数 (objective function)(通常是损失函数
)的值尽可能小。 - 方法: 使用优化算法 (optimization algorithms) 来系统地搜索参数空间,找到能使目标函数最小化的参数值。
15. 连续优化的主要分支
- 无约束优化 (Unconstrained Optimization):
- 这是我们在深度学习中最常遇到的情况。参数的取值没有任何限制。
- 核心原理: 寻找“山谷”的最低点。梯度
指向“上坡”最陡峭的方向,因此我们沿着负梯度 的方向移动,即“下山”。
- 约束优化 (Constrained Optimization):
- 参数的取值受到一些等式或不等式条件的限制。例如,某些参数必须大于零,或者所有参数的平方和必须等于1。
- 这需要引入更复杂的数学工具(如拉格朗日乘子法)来处理。
- 凸优化 (Convex Optimization):
- 这是一个非常特殊的类别,无论是无约束还是有约束问题都可能属于凸优化。
- 特点: 目标函数是一个凸函数(形状像一个完美的“碗”),且可行域是凸集。
- 巨大优势: 对于凸优化问题,任何局部最小值都必然是全局最小值。这意味着我们不必担心优化算法会卡在“不够好”的次优解中。梯度下降等简单算法就能保证找到全局最优解。
16. 全局最小值 vs. 局部最小值
对于非凸函数(如大多数深度学习的损失函数),优化算法通常只能保证找到局部最小值 (local minimum),而不能保证找到全局最小值 (global minimum)。
-
临界点/驻点 (Stationary Points):
- 一个函数梯度为零的点(
)被称为临界点。这些点是所有极值点(最小值、最大值)和鞍点的候选点。 - 我们可以通过求解
这个方程来解析地找到所有临界点。
- 一个函数梯度为零的点(
-
二阶导数测试 (Second Derivative Test):
- 在找到一个临界点后,我们可以利用二阶导数(对于多变量函数,即海森矩阵)来判断它的类型:
- 二阶导数 > 0 (或海森矩阵正定): 该点是局部最小值。
- 二阶导数 < 0 (或海森矩阵负定): 该点是局部最大值。
- 二阶导数 = 0 (或海森矩阵不定): 情况不确定,可能是鞍点或拐点。
- 在找到一个临界点后,我们可以利用二阶导数(对于多变量函数,即海森矩阵)来判断它的类型:
-
初始化的重要性:
- 由于存在多个局部最小值,从不同的初始参数点开始优化,可能会收敛到不同的局部最小值,其对应的损失值也不同。
- 在非凸优化中,选择一个好的初始化点,或者多次从不同点开始训练,是寻找更好解的常用策略。
-
解析解 vs. 迭代解:
- 对于非常简单的函数(如低阶多项式),我们可以通过解析地解方程
来找到所有临界点。 - 但在机器学习中,损失函数极其复杂,解析求解是不可能的。因此,我们必须依赖像梯度下降这样的迭代算法,从一个初始点出发,一步步地“走”向一个最小值点。
- 对于非常简单的函数(如低阶多项式),我们可以通过解析地解方程
17. 使用梯度下降进行优化 (Optimization Using Gradient Descent)
梯度下降法是解决上述优化问题最基本、也是最重要的迭代算法之一。它是绝大多数现代优化算法的基石。
17.1 梯度下降概览
机器学习 (Machine Learning)#2.3.1 核心优化算法:梯度下降及其变体
-
问题设定: 我们要解决无约束优化问题:
其中
是一个可微的目标函数(例如,机器学习中的损失函数)。 -
核心思想:
- 从一个随机的初始点
开始。 - 计算函数在该点的梯度
。 - 我们知道,梯度指向函数值上升最快的方向。
- 因此,我们沿着梯度的反方向
移动一小步。这个方向是函数值下降最快的方向。 - 到达一个新的点
,并重复这个过程,直到收敛。
- 从一个随机的初始点
-
直观比喻: 想象一个身处在漆黑山谷中的登山者想要下到谷底。他看不见全局地形,但他可以感知脚下哪一个方向最陡峭。他每一步都选择朝最陡峭的下坡方向走一小步,最终就能走到一个局部的谷底。
17.2 梯度下降算法
-
更新规则:
对于一个多元函数,梯度下降的迭代更新步骤可以写成: 其中:
是第 i步的参数位置。是在点 计算出的梯度(一个 的行向量)。 将梯度转置成一个 的列向量,以便与列向量 进行向量减法。 是第 i步的学习率 (learning rate) 或步长 (step-size),它控制了我们每一步“下山”的距离。
-
算法流程:
- 选择一个初始点
。 - For i = 0, 1, 2, ... do:
- 计算梯度:
- 更新参数:
- End For
- 算法在满足某个停止条件时(例如,梯度变得非常小,或者迭代次数达到上限)终止。
- 选择一个初始点
-
收敛性:
只要步长选择得当(不能太大也不能太小),这个迭代序列产生的函数值会单调下降: ,并最终收敛到一个局部最小值。
17.3 步长/学习率 (Step-Size / Learning Rate) 的选择
机器学习 (Machine Learning)#2.3.2.3 优化再进阶:自适应学习率 (Adaptive Learning Rate)
在梯度下降的更新规则 x_i+1 = x_i - γ_i * g_i 中,步长 γ (通常在机器学习中称为学习率) 的选择至关重要,它直接决定了算法的性能和收敛性。
-
步长
γ的作用: 它决定了我们每一步沿着负梯度方向移动的距离。 -
选择不当的后果:
- 步长过小 (Too small): 算法的收敛速度会非常缓慢。就像下山时每一步只挪动一小寸,需要无数步才能到达谷底。
- 步长过大 (Too large): 算法可能会**“矫枉过正” (overshoot)**,即一步迈得太大,直接跨过了谷底,到达了对面更高的山坡上。这会导致算法在最小值点附近剧烈震荡,无法收敛,甚至可能发散(损失值越来越大)。
-
解决方案:
- 动量法 (Momentum methods): 引入“惯性”的概念,平滑更新方向,抑制在陡峭方向上的震荡。
- 自适应梯度方法 (Adaptive gradient methods): 如前所述的 Adagrad、RMSProp、Adam 等,它们能根据函数局部的几何特性,在每次迭代中自动调整每个参数的学习率。
17.4 调整步长的启发式策略 (Heuristics)
在实践中,有一些简单的启发式方法可以用来动态调整步长 γ:
-
如果更新后,函数值反而增加了 (
): - 问题: 这说明步长
γ太大了,导致了“矫枉过正”。 - 策略: 撤销 (undo) 这一步的更新(退回到
),然后减小步长 γ(例如,γ = γ / 2),再重新尝试更新。
- 问题: 这说明步长
-
如果更新后,函数值减小了 (
): - 情况: 这是一个成功的更新步骤。
- 策略: 我们可以稍微增大步长
γ(例如,γ = γ * 1.1),以期在后续步骤中能更快地收敛。
- 评价: 尽管“撤销”步骤看起来有些浪费计算资源,但这种“试探并调整”的策略能够保证函数值在迭代过程中是单调下降的,从而确保算法最终能收敛到一个局部最小值。
17.5 示例:用梯度下降求解线性方程组
梯度下降不仅可以用于机器学习中的复杂损失函数,也可以用来求解经典的线性方程组 Ax = b。
-
问题转化: 我们可以将求解
Ax = b的问题,转化为一个优化问题。我们定义一个目标函数,当这个函数达到最小值时,其解x就是原方程组的解。一个自然的选择就是最小化均方误差: -
展开与求梯度:
利用我们之前学过的向量微积分法则,可以计算出这个函数对
x的梯度: -
应用梯度下降:
- 我们可以用这个梯度来构建梯度下降的更新规则:
(注意梯度需要转置成列向量) - 通过迭代,
x就会逐渐收敛到线性方程组的解(或在无解时的最小二乘解)。
- 我们可以用这个梯度来构建梯度下降的更新规则:
-
与解析解的对比:
对于这个特殊的二次优化问题,我们其实有一个解析解 (analytic solution)。只需将梯度设为零即可:这就是我们在线性回归中遇到的正规方程 (Normal Equation)。但在很多情况下(例如矩阵
A巨大),迭代法可能比直接求逆更高效。
18. 动量梯度下降法 (Gradient Descent with Momentum)
机器学习 (Machine Learning)#2.3.1.3 动量法 (Momentum)
标准梯度下降法虽然直观,但在某些常见的优化场景下效率低下。动量法是对其一个非常重要且有效的改进。
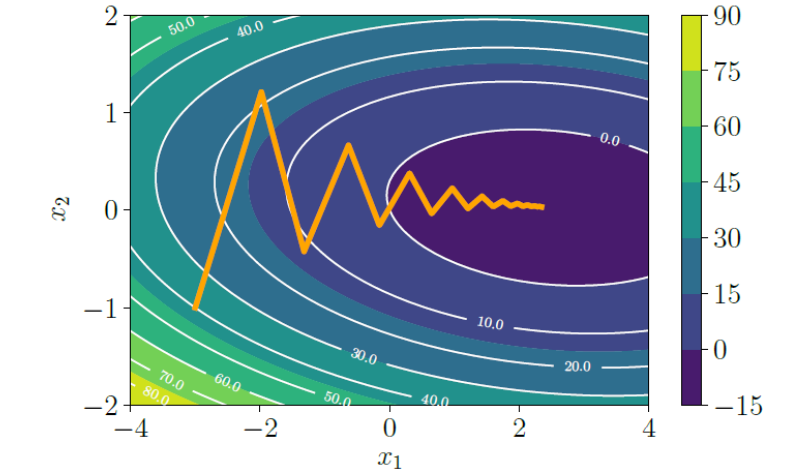
18.1 引入动量的动机
- 问题: 当优化的损失曲面具有病态曲率 (poorly scaled curvature) 时(例如,一个狭长、陡峭的“山谷”),标准梯度下降会表现得很差。
- 现象: 算法的更新路径会在狭窄的“山谷”两壁之间来回**“之”字形震荡 (zig-zag)**,而在通向谷底的平缓方向上,每一步前进的距离又非常小。这导致收敛速度极其缓慢。
- 解决方案: 我们希望找到一种方法,能够抑制在陡峭方向上的震荡,同时加速在平缓方向上的前进。
18.2 动量法的核心思想
- 引入“惯性”或“记忆”: 动量法为梯度下降的更新步骤增加了一个记忆项,使其“记住”上一步的更新方向。
- 直观比喻: 想象一个重球 (heavy ball) 从一个表面上滚下来。
- 这个重球因为有惯性 (momentum),所以不愿意轻易改变它的运动方向。
- 当它在狭窄山谷的两壁之间来回滚动时,惯性会抑制 (dampen) 这种震荡。
- 当它沿着平缓的谷底方向滚动时,由于方向一致,惯性会使其加速 (accelerate) 下滑。
- 效果: 动量法通过平滑更新路径,有效地抑制了震荡,从而实现了更快的收敛。
18.3 动量法的更新规则
动量法通过维护一个梯度的移动平均值 (moving average) 来实现“记忆”功能。
在每一次迭代 i,更新步骤是当前梯度和之前更新量的线性组合:
-
更新规则:
其中:
是上一步的更新向量。 是动量参数 (momentum parameter)。它控制了“记忆”的权重。一个常见的设置是 。
-
另一种等价形式 (更常用):
我们可以定义一个“速度”向量,它累积了梯度的历史信息: 是当前更新的方向和大小,它由两部分组成:一部分是衰减后的旧速度 ,另一部分是当前梯度 。
动量法的优势:
- 加速收敛: 在梯度方向基本一致的平缓区域,动量会累积,使得更新步长越来越大。
- 抑制震荡: 在梯度方向来回变化的的陡峭区域,动量项的正负号会交替出现,从而相互抵消,减小了更新步长的震荡幅度。
- 处理噪声: 当梯度本身是带噪声的,或者只是一个近似值时(例如,在随机梯度下降中),动量法通过对历史梯度进行平均,能够有效地平滑掉噪声,使得更新方向更加稳定。
动量法是现代深度学习优化器(如 SGD with Momentum, Adam)的一个核心组成部分。
19. 随机梯度下降 (Stochastic Gradient Descent, SGD)
机器学习 (Machine Learning)#2.3.1.2 批量大小的选择 (The Choice of Batch Size)
在处理大规模数据集时,标准的(批次)梯度下降法会遇到一个致命的瓶颈:计算成本。随机梯度下降及其变体是解决这个问题的核心方法。
19.1 从批次梯度下降到随机梯度下降
-
目标函数的形式: 在机器学习中,总的损失函数
通常是所有 N 个训练样本各自损失 的和或平均值: -
批次梯度下降 (Batch Gradient Descent):
- 这是我们之前讨论的标准梯度下降。它在每一步更新时,都使用整个训练集来计算精确的梯度。
- 瓶颈: 当数据集非常大时(例如,N有数百万),计算一次完整的梯度(需要遍历所有N个样本)会变得极其耗时,使得训练过程非常缓慢。
- 这是我们之前讨论的标准梯度下降。它在每一步更新时,都使用整个训练集来计算精确的梯度。
-
随机梯度下降 (SGD) 的核心思想:
- 我们真的需要精确的梯度才能下山吗?不一定。一个大致指向下山方向的“便宜”的梯度近似值,可能已经足够好了。
- “随机”的含义: SGD 使用一个随机的、带噪声的梯度估计来代替真实的梯度。
- 理论保证: 只要这个梯度估计是无偏的 (unbiased)(即它的期望值等于真实梯度),并且其概率分布满足一定条件,那么SGD在理论上仍然可以保证收敛。
19.2 小批量 (Mini-batch) 与随机梯度下降
-
梯度估计的无偏性:
- 真实梯度是
。 - 如果我们从整个数据集中随机抽取一个小批量 (mini-batch) 的样本子集
(大小为 ),那么基于这个小批量的平均梯度 就是真实梯度的一个无偏估计。 - 因此,基于小批量样本的更新在方向上是“平均正确”的。
- 真实梯度是
-
两种主要的SGD变体:
- 小批量梯度下降 (Mini-batch Gradient Descent):
- 这是在实践中最常用的方法。
- 在每次迭代时,随机选择一个小批量(例如,大小为
)的数据。 - 使用这个小批量的平均梯度进行更新:
- 纯随机梯度下降 (Stochastic Gradient Descent, SGD):
- 这是小批量大小
的极端情况。 - 在每次迭代时,只随机选择一个数据点。
- 只使用这一个数据点的梯度进行更新:
- 这是小批量大小
- 小批量梯度下降 (Mini-batch Gradient Descent):
1.9.3 批量大小 (Batch Size) 的权衡与实践
-
为什么使用近似梯度?
- 计算效率: 在每次迭代中,计算成本与批量大小成正比。使用小批量可以极大地减少每次更新的计算时间。
- 硬件利用: 现代硬件(如GPU/TPU)为并行计算进行了优化。使用小批量(而不是单个样本)可以更好地利用硬件的并行处理能力,实现高效的向量化计算。
-
批量大小的权衡:
- 大的小批量 (Larger mini-batches):
- 优点: 梯度估计的方差更小,更新方向更稳定,收敛路径更平滑。能更好地利用硬件并行性。
- 缺点: 每次迭代的计算成本更高。
- 小的小批量 (Smaller mini-batches, 包括 m=1):
- 优点: 每次迭代的计算成本非常低,更新速度快。
- 缺点: 梯度估计带有很大的噪声(方差大),导致收敛路径非常震荡。
- 一个意外的好处: 这种噪声有时可以帮助优化算法**“跳出”不好的局部最小值或鞍点**,起到一种正则化的效果,可能有助于找到泛化性能更好的解。
- 大的小批量 (Larger mini-batches):
-
结论: 小批量梯度下降在计算效率和收DENOISE稳定性之间取得了很好的平衡,是目前训练大规模机器学习模型(特别是深度神经网络)的标准和首选方法。
第九讲:约束优化与拉格朗日乘子,凸优化
第一部分:约束优化与拉格朗日乘子 (Constrained Optimization and Lagrange Multipliers)
在上一讲中,我们主要讨论了无约束优化,即在整个参数空间中自由地寻找函数的最小值。然而,在许多实际问题中,参数的取值会受到各种约束 (constraints) 的限制。
1. 约束优化问题
- 从无约束到有约束:
- 无约束优化:
- 约束优化:
- 无约束优化:
- 问题设定: 我们要在满足一系列不等式约束条件
的可行域 (feasible region) 内,找到使目标函数 最小的解。 - 普适性: 目标函数
和约束函数 在一般情况下都可以是非凸的。 - 实际应用:
- 在概率模型中,所有概率之和必须等于1。
- 在某些模型中,权重参数必须是非负的。
- 在资源分配问题中,总消耗不能超过预算。
2. 处理约束的朴素思想与拉格朗日乘子的动机
-
指示函数法 (Indicator Function Approach):
- 一个最直接但不实用的想法是,将约束转化为一个惩罚项,加到目标函数中。我们可以定义一个新的目标函数
: - 其中,
是一个无限阶跃函数 (infinite step function): - 效果: 如果任何一个约束被违反(即
),目标函数的值就会变成无穷大。这样,最小化 的过程就会自动地迫使解满足所有约束。 - 缺点: 这个新的目标函数
是非连续、不可微的,存在一个“无限高的墙”,这使得使用基于梯度的数值优化方法变得极其困难。
- 一个最直接但不实用的想法是,将约束转化为一个惩罚项,加到目标函数中。我们可以定义一个新的目标函数
-
拉格朗日乘子的动机:
- 为了克服指示函数的缺点,我们需要一种更“温和”的方式来处理约束。
- 拉格朗日乘子法通过将这种“硬约束”(无限高的墙)替换为一个**“软”的、线性的惩罚项**,使得问题在数学上变得更容易处理(更平滑、可微)。
3. 拉格朗日函数与拉格朗日乘子
- 引入拉格朗日乘子:
- 对于每一个不等式约束
,我们都引入一个与之对应的拉格朗日乘子 (Lagrange multiplier) ,并要求 。
- 对于每一个不等式约束
- 定义拉格朗日函数 (The Lagrangian):
我们将原始的目标函数和带权重的约束函数结合起来,构造一个新的函数,称为拉格朗日函数:或者用向量形式表示: 其中 是所有约束函数构成的向量, 是所有拉格朗日乘子构成的向量。 - 作用: 拉格朗日函数巧妙地将一个有约束的优化问题,转化为了一个关于
和 的、更易于分析的函数。我们将在后面看到,通过分析这个函数的性质,我们可以找到原约束问题的解。
4. 拉格朗日对偶性:原问题与对偶问题
拉格朗日乘子法最强大的地方在于它引入了对偶性 (Duality)。它允许我们将一个原始的、可能很难解决的优化问题(原问题),转化为一个与之相关的、但可能更容易解决的新问题(对偶问题)。
-
原问题 (Primal Problem):
这就是我们最初想要解决的带约束的优化问题。这里的变量
被称为原变量 (primal variables)。 -
拉格朗日函数 (Lagrangian):
我们已经定义过,它是连接原问题和对偶问题的桥梁。 -
对偶函数 (Dual Function):
对偶函数是通过最小化拉格朗日函数 关于原变量 得到的结果。 注意,在计算
时,我们将 视为固定的常数。 的结果是一个只依赖于 的函数。 -
对偶问题 (Dual Problem):
对偶问题就是去最大化这个对偶函数。 这里的变量
被称为对偶变量 (dual variables)。
5. 弱对偶性与极小化极大不等式
原问题和对偶问题之间存在一个基本且恒成立的关系,称为弱对偶性 (Weak Duality)。
-
原问题的等价形式:
我们可以将原约束问题巧妙地重写为一个“极小化-极大化”问题:为什么等价? 考虑内部的
: - 如果
违反了某个约束(例如 ),那么我们可以让对应的 ,这会使得 趋向于无穷大。 - 如果
满足所有约束(即所有 ),那么为了最大化 ,由于 ,我们应该让所有 项尽可能大。因为 ,所以这项的最大值是 0(当 或 时取到)。 - 因此,
的结果是:如果 可行,则为 ;如果 不可行,则为 。 - 那么对这个结果再取
,就恰好等价于在可行域内最小化 ,这正是原问题的定义。
- 如果
-
极小化极大不等式 (Minimax Inequality):
对于任何函数,交换min和max的顺序,会得到一个不等式关系: -
弱对偶性:
将我们之前的定义代入这个不等式:- 不等式的左边是原问题的最优值。
- 不等式的右边是对偶问题的最优值(因为
就是对偶函数 )。 - 因此,我们得到了弱对偶性定理:
结论: 对偶问题的最优解
永远是原问题最优解 的一个下界 (lower bound)。
6. 为什么对偶性有用?
-
提供下界与最优性证明:
- 对偶问题提供了一个衡量我们当前解有多好的标尺。原问题的任何一个可行解的目标函数值
与对偶问题的任何一个可行解的目标函数值 之间的差 ,被称为对偶间隙 (duality gap)。 - 这个间隙告诉我们,我们找到的
最多比全局最优解 大多少。如果这个间隙为零,我们就找到了全局最优解。
- 对偶问题提供了一个衡量我们当前解有多好的标尺。原问题的任何一个可行解的目标函数值
-
计算上的便利性:
- 在很多情况下,对偶问题比原问题更容易求解。
- 例如,对偶问题可能会有更少的变量,更好的数学性质(例如,对偶函数总是凹函数,无论原问题是否是凸的),或者具有可以分解为多个子问题的优美结构。
- 在许多大规模机器学习问题中(如支持向量机 SVM),求解其对偶问题远比直接求解原问题高效。
-
强对偶性 (Strong Duality):
- 在某些“良好”的情况下(特别是对于凸优化问题,并满足一些约束规范,如Slater条件),弱对偶性中的不等号可以取等号,即
。 - 这就是强对偶性。当强对偶性成立时,求解对偶问题就完全等价于求解原问题。我们可以通过解决更容易的对偶问题来获得原问题的最优解。
- 在某些“良好”的情况下(特别是对于凸优化问题,并满足一些约束规范,如Slater条件),弱对偶性中的不等号可以取等号,即
7. 求解拉格朗日对偶问题 (可微情况)
当我们处理的函数
求解流程:
-
构造拉格朗日函数:
写出拉格朗日函数。 -
求解对偶函数
: - 回忆对偶函数的定义:
。 - 这是一个关于
的无约束优化问题。为了找到最小值,我们将 对 求梯度,并令其为零: - 从这个方程中,解出最优的
,这个解通常会是 的一个函数,即 。
- 回忆对偶函数的定义:
-
得到对偶函数表达式:
- 将上一步解出的
代回到拉格朗日函数 中,消去 。 - 得到的结果就是一个只包含对偶变量
的函数,这正是对偶函数 的显式表达式。
- 将上一步解出的
-
求解对偶问题:
- 现在我们有了对偶函数
,我们需要解决对偶问题: - 这是一个新的、关于
的约束优化问题。我们可以使用梯度上升法或其他优化技术来求解它。
- 现在我们有了对偶函数
8. 处理等式约束 (Equality Constraints)
到目前为止,我们只考虑了不等式约束
问题形式:
处理方法:
一个等式约束
我们可以为这两个不等式分别引入拉格朗日乘子
现在,我们令
结论与规则总结:
这导出了一个非常重要的规则,用于区分不同类型约束所对应的拉格朗日乘子:
- 不等式约束 (
): - 其对应的拉格朗日乘子
必须是非负的 ( )。
- 其对应的拉格朗日乘子
- 等式约束 (
): - 其对应的拉格朗日乘子
是无符号约束的 (unconstrained),它可以是任何实数。
- 其对应的拉格朗日乘子
在构造包含两种约束的拉格朗日函数时,这个区别至关重要:
并且在求解对偶问题时,我们需要满足
第二部分:凸优化 (Convex Optimization)
在一般性的(非凸)优化问题中,我们通常只能保证找到局部最优解。然而,有一类特殊的优化问题,它具有非常优美的性质,能够保证我们找到的解就是全局最优解。这就是凸优化。
9. 凸优化与强对偶性
-
定义: 一个优化问题如果满足以下两个条件,就被称为凸优化问题 (convex optimization problem):
- 目标函数
是一个凸函数。 - 所有约束函数
定义的可行域是一个凸集。
- 目标函数
-
凸优化的巨大优势:
- 任何局部最优解都是全局最优解: 在凸优化问题中,不存在“不好”的局部最小值。只要你找到了一个“谷底”,它就一定是整个地形的最低点。这极大地简化了优化的目标。
- 强对偶性通常成立: 对于凸优化问题(并满足一些温和的额外条件,如Slater条件),强对偶性 (strong duality) 成立。这意味着原问题的最优值与对偶问题的最优值完全相等 (
)。因此,我们可以通过求解更容易的对偶问题来获得原问题的精确解。
为了理解凸优化,我们首先需要定义什么是凸集和凸函数。
10. 凸集 (Convex Set)
-
定义: 一个集合
被称为凸集,如果对于集合中任意两点 ,以及任意满足 的标量 ,它们的凸组合点也位于集合 中: -
几何直观: 连接集合内任意两点的线段,必须完全包含在该集合内部。如果能找到任何一条线段“穿出”了集合的边界,那么这个集合就不是凸的。
-
示例:
- 凸集: 实心多边形、球体、半空间、直线、平面等。
- 非凸集: 空心的环、月牙形、任何有“凹陷”或“洞”的形状。
11. 凸函数 (Convex Function)
-
定义: 一个定义在凸集上的函数
被称为凸函数,如果对于其定义域内的任意两点 ,以及任意满足 的标量 ,都满足以下不等式: -
几何直观: 这个不等式的几何意义是:函数图像上任意两点之间的弦 (chord),永远位于函数图像的上方(或与之接触)。一个凸函数的图像形状就像一个“碗”。
-
凹函数 (Concave Function): 如果一个函数
是凸的,那么 就是一个凹函数。其图像形状像一个“帽子”,弦位于图像的下方。
12. 连接凸函数与凸集
凸函数和凸集是凸优化的一体两面,它们之间有着紧密的联系。
-
约束定义可行集: 在约束优化中,像
这样的约束,其本质是定义了一个水平集 (level set)。如果约束函数 是一个凸函数,那么它定义的可行域 必然是一个凸集。多个凸集的交集仍然是凸集,因此由多个凸函数约束定义的可行域也是凸的。 -
上境图 (Epigraph):
- 一个函数
的上境图是位于其图像上方的所有点的集合,即 {(x, t) | t ≥ f(x)}。 - 几何直观: 想象一个碗状的凸函数图像,向这个“碗”里倒满水,水和碗共同占据的空间就是它的上境图。
- 重要性质: 一个函数是凸函数的充分必要条件是,它的上境图是一个凸集。这个性质为分析和解决凸优化问题提供了重要的几何工具。
- 一个函数
13. 凸性与导数的关系
对于可微函数,我们可以用其导数来更方便地判断其是否为凸函数。
-
一阶条件 (First-order Condition):
对于一个可微函数,它是凸函数的充要条件是: - 几何意义: 函数在任意点
处的切线(或切平面),永远位于整个函数图像的下方。
- 几何意义: 函数在任意点
-
二阶条件 (Second-order Condition):
对于一个二阶可微的函数,它是凸函数的充要条件是,其海森矩阵 (Hessian Matrix) 在其定义域内处处是半正定的 (positive semidefinite)。 - 几何意义: 函数在所有方向上的曲率 (curvature) 都是非负的,即函数图像处处“向上弯曲”。
14. 保持凸性的运算
凸性在很多运算下是封闭的,这使得我们可以通过组合简单的凸函数来构建更复杂的凸函数。
- 非负数缩放: 如果
是凸函数,且 ,那么 也是凸函数。 - 求和: 如果
和 都是凸函数,那么它们的和 也是凸函数。 - 推广: 任意多个凸函数的非负加权和
(其中 )仍然是凸函数。
- 推广: 任意多个凸函数的非负加权和
15. 凸优化问题的正式总结
一个约束优化问题:
被称为凸优化问题,如果它满足:
- 目标函数
是一个凸函数。 - 所有不等式约束函数
都是凸函数。 - 所有等式约束函数
都是仿射函数 (affine),即 。(因为只有仿射函数的水平集 才能保证是凸集)。
16. 示例
16.1 最小二乘问题
经典的无约束最小二乘问题 (Least Squares Problem) 是一个典型的凸优化问题。
- 证明其凸性:
- 我们将目标函数
展开: - 这是一个关于
的二次函数。我们计算它对 的海森矩阵(二阶导数): - 我们来验证这个海森矩阵是否是半正定的。对于任意向量
: - 因为向量范数的平方
永远是大于等于 0 的,所以 是半正定的。 - 根据二阶条件,我们证明了最小二乘的目标函数是一个凸函数。由于没有约束,所以这是一个无约束凸优化问题。
- 我们将目标函数
16.2 最小范数问题 (Minimum Norm Problem)
另一个经典的凸优化问题是最小范数问题。
问题形式:
(最小化
直观解释: 在所有满足线性方程组
这是一个凸优化问题吗?
根据凸优化问题的定义,我们需要验证两点:
- 目标函数
是一个凸函数。 - 约束定义的可行域
是一个凸集。
证明 1: 目标函数
- 一般性结论: 所有的范数 (Norms) 都是凸函数。
- 证明: 我们需要验证范数是否满足凸函数的定义:
将 代入,我们需要证明: - 利用范数的三角不等式 (Triangle Inequality):
。 - 利用范数的正齐次性 (Absolute Homogeneity):
。 - 因为我们已知
,所以 且 。 - 结合以上步骤,我们证明了
。 - 因此,欧几里得范数(以及所有范数)都是凸函数。
- 利用范数的三角不等式 (Triangle Inequality):
证明 2: 可行域
- 一般性结论: 由仿射函数定义的等式约束,其可行域是一个凸集。(这样的集合也称为仿射集 (Affine Set))。
- 证明: 我们需要验证该集合是否满足凸集的定义。
- 设集合为
。 - 从
中任意取出两个点 和 。根据定义,我们知道: - 现在,我们考虑这两点的任意一个凸组合点
,其中 。我们要检查 是否也属于集合 。 - 我们将
作用于 : - 由于
,这表明 也满足约束条件,因此 。 - 这就证明了集合
是一个凸集。
- 设集合为
最终结论:
由于最小范数问题的目标函数是凸的,且其约束定义的可行域也是一个凸集,因此最小范数问题是一个标准的凸优化问题。
第三部分:概率与分布 (Probability and Distributions)
概率论是机器学习的基石,它为我们提供了一套在不确定性下进行推理和建模的数学语言。
17. 概率论的核心概念
-
概率空间 (Probability Space): 这是量化概率的基础框架,它由三个部分组成:
- 样本空间 (Sample Space)
: 一个实验 (experiment) 所有可能结果 (outcomes) 的集合。 - 示例: 抛掷两枚硬币,
。
- 示例: 抛掷两枚硬币,
- 事件空间 (Event Space)
: 样本空间 的子集构成的集合。每一个子集被称为一个事件 (event)。 - 示例: 事件“至少有一次正面朝上”对应于子集
。
- 示例: 事件“至少有一次正面朝上”对应于子集
- 概率 (Probability)
: 一个函数,它为事件空间中的每一个事件 指派一个数值 ,表示事件 发生的概率。
- 样本空间 (Sample Space)
-
随机变量 (Random Variables):
- 定义: 一个随机变量
是一个函数,它将样本空间 中的每一个结果映射到一个更方便(通常是数值)的空间 中。 - 作用: 它为我们提供了一种用数字来描述随机实验结果的方式。
- 示例: 在抛掷两枚硬币的实验中,我们可以定义一个随机变量
为“正面朝上的次数”。 - 这里的目标空间是
。
- 定义: 一个随机变量
-
分布/定律 (Distribution/Law):
- 它描述了与一个随机变量所有可能取值相关联的概率。例如,上面例子中
的分布就是 的值。
- 它描述了与一个随机变量所有可能取值相关联的概率。例如,上面例子中
18. 事件的关系与概率运算
我们可以使用维恩图 (Venn Diagrams) 来直观地表示事件之间的关系。
-
“与” (AND, 交集
): - 表示事件 A 和 事件 B 同时发生的区域。
- 其概率为联合概率 (Joint Probability),记为
或 。 - 独立性: 如果事件 A 和 B 是独立的 (independent),则
。 - 互斥性: 如果 A 和 B 不可能同时发生(交集为空),则
。
-
“或” (OR, 并集
): - 表示事件 A 或 事件 B(或两者都)发生的区域。
- 其概率由加法法则给出:
-
条件概率 (Conditional Probability):
- 表示在事件 B 已经发生的条件下,事件 A 发生的概率。
- 定义为:
- 几何直观: 它可以被看作是在 B 事件发生的范围内,A 事件也发生的部分所占的比例。
19. 离散随机变量与概率质量函数 (PMF)
对于一个取值为离散的随机变量,其分布由概率质量函数 (Probability Mass Function, PMF) 描述。PMF 为该随机变量的每一个可能取值,都指派一个特定的概率。
- 示例:不公平硬币抽样
- 实验: 从一个袋子中有放回地抽取两次硬币,袋中有美元($)和欧元(e)两种硬币。每次抽到美元的概率是 0.3。
- 随机变量:
= “抽到美元的次数”。 的可能取值是 {0, 1, 2}。 - 计算 PMF:
- 检验: 所有可能结果的概率之和为
,符合概率公理。 - 这组概率值
就完整地定义了随机变量 的概率分布。
20. 通过随机变量和原像来理解概率
随机变量
-
核心思想:
我们通常更关心随机变量的取值(例如,“得到1个正面的概率是多少?”),而不是原始的实验结果(例如,“得到{ht, th}的概率是多少?”)。
一个随机变量取某个特定值的概率,等于所有能导致这个值的原始实验结果的概率之和。 -
原像 (Pre-image):
- 对于目标空间
中的一个子集(事件) ,其原像 是指样本空间 中所有能够被随机变量 映射到 中的原始结果的集合。
- 对于目标空间
-
分布的正式定义:
随机变量取值于集合 内的概率 ,被定义为其原像 在原始样本空间上发生的概率: 这个函数
被称为随机变量 的分布 (distribution)。 -
示例:
- 实验: 抛掷两枚公平硬币。
,每个结果的概率是 1/4。 - 随机变量:
= 正面朝上的次数。 - 事件: 我们关心事件
,即“至少有一次正面朝上”。 - 原像:
是所有能使 取值为1或2的原始结果,即 。 - 计算概率:
- 实验: 抛掷两枚公平硬币。
21. 随机变量的类型
随机变量的类型由其目标空间
-
离散随机变量 (Discrete Random Variable):
- 其目标空间
是有限的 (finite) 或可数无穷的 (countably infinite)。 - 示例: 抛硬币得到正面的次数(取值为 {0, 1, 2, ...}),掷骰子的点数(取值为 {1, 2, 3, 4, 5, 6})。
- 其目标空间
-
连续随机变量 (Continuous Random Variable):
- 其目标空间
是不可数的,通常是一个区间或整个实数轴 (或高维空间 )。 - 示例: 一个人的精确身高(理论上可以取某个区间内的任何值),一次测量的误差。
- 其目标空间
22. 描述概率分布的函数
我们使用不同的函数来精确描述不同类型随机变量的分布。
-
对于离散随机变量:
- 我们使用概率质量函数 (Probability Mass Function, PMF)。
- PMF 直接给出了随机变量
取到某个特定值 的概率: 。
-
对于连续随机变量:
- 单个点的概率为零(例如,身高恰好等于1.75000...米的概率是0)。因此我们关心的是变量落入某个区间的概率,例如
。 - 我们通常使用累积分布函数 (Cumulative Distribution Function, CDF) 来描述其分布。
- CDF 给出了随机变量
的值小于或等于某个特定值 的概率: 。
- 单个点的概率为零(例如,身高恰好等于1.75000...米的概率是0)。因此我们关心的是变量落入某个区间的概率,例如
-
备注:
- 单变量分布 (Univariate Distribution): 描述单个随机变量的分布。
- 多变量分布 (Multivariate Distribution): 描述一个随机向量(包含多个随机变量)的联合分布。
第四部分:离散概率 (Discrete Probabilities)
本部分将重点讨论当存在多个离散随机变量时,我们如何描述和计算它们的概率。
23. 联合概率与边缘概率
当我们的系统涉及多个随机变量时(例如,一个人的身高和体重),我们需要描述它们同时取特定值的概率。
-
联合概率 (Joint Probability):
- 对于两个离散随机变量
和 ,它们的联合概率是指 取特定值 并且 取特定值 的概率。 - 记法:
。这等价于事件的交集概率 。 - 计算: 如果我们有一个包含
次实验结果的数据集,其中状态 出现了 次,那么联合概率可以通过频率来估计: - 可视化: 两个离散随机变量的联合概率分布可以用一个二维表格(或矩阵) 来表示,表格的每个单元格
存放着概率值 。
- 对于两个离散随机变量
-
边缘概率 (Marginal Probability):
- 有时,我们只关心其中一个变量的概率,而不关心另一个变量的取值。这个概率被称为边缘概率。
- 计算: 要获得变量
的边缘概率 ,我们需要对所有可能的 值求和(即“边缘化”掉变量Y),这个过程在联合概率表中体现为对列求和。 - 同样,要获得
的边缘概率 ,我们需要对行求和: - 从计数表计算:
是第 i列的总计数。是第 j行的总计数。
-
独立性:
- 如果随机变量
和 是独立的,那么它们的联合概率等于它们边缘概率的乘积: - 反之,如果这个等式对所有
都成立,那么 和 就是独立的。
- 如果随机变量
24. 条件概率
- 定义: 条件概率
是指在已知 的值为 的前提下, 的值为 的概率。 - 计算:
- 根据条件概率的通用定义:
- 从计数表计算: 这个计算非常直观。它等于在 “
” 这一列中,“ ” 这个单元格的计数,除以这一列的总计数。 - 同样地:
- 根据条件概率的通用定义:
25. 符号与归一化
- PMF 记法: 对于多变量离散分布,我们通常用小写字母
p来表示概率质量函数。- 联合概率:
- 边缘概率:
- 条件概率:
- 联合概率:
- 分布记法: 符号
表示随机变量 服从概率分布 。 - 归一化 (Normalization):
- 一个合法的概率分布,其所有可能结果的概率之和必须等于 1。
- 对于边缘概率:
。 - 对于联合概率:
。 - 对于条件概率:给定一个
,所有可能的 的条件概率之和必须为 1: 。
第五部分:连续概率 (Continuous Probabilities)
现在,我们将概率论的思想从离散的、可数的事件,推广到连续的、不可数的事件上。
26. 概率密度函数 (Probability Density Function, PDF)
对于连续随机变量,我们无法讨论它取某个精确值的概率(因为这个概率为零),而是讨论它落入某个区域的概率。概率密度函数 (PDF) 就是用来描述这种概率分布的工具。
-
定义: 一个函数
如果满足以下两个条件,就被称为一个概率密度函数 (PDF): - 非负性: 对于所有
,都有 。 - 归一化: 函数在整个定义域上的积分必须等于 1。
- 非负性: 对于所有
-
用 PDF 计算概率:
- 单变量情况 (
): 一个连续随机变量 的值落入区间 内的概率,等于其 PDF 在该区间上的定积分,也就是函数曲线下方的面积。 - 多变量情况 (
): 一个随机向量 的值落入某个区域 的概率,等于其联合 PDF 在该区域上的多重积分,也就是函数曲面下方的体积。
- 单变量情况 (
-
重要说明:
- PDF 本身的值不是概率。它代表的是在该点附近单位体积(或面积、长度)内的概率密度。
- PDF 的值可以大于 1。只要它在整个定义域上的总积分为1即可。
- 对于连续随机变量,
。
27. 累积分布函数 (Cumulative Distribution Function, CDF)
CDF 是另一种描述概率分布的通用工具,它对离散和连续随机变量都适用,并且能很自然地从单维推广到多维。
-
定义: 对于一个多维实值随机变量
,其累积分布函数 (CDF) 定义为随机向量 的所有分量都小于或等于对应阈值 的联合概率: -
CDF 与 PDF 的关系:
对于连续随机变量,CDF 是其 PDF 从负无穷到当前点的多重积分。这正是你指出的那个重要的多重积分公式:反之,联合 PDF 是联合 CDF 的混合偏导数:
。 -
备注: 存在一些没有对应 PDF 的 CDF。例如,离散随机变量的CDF是阶跃函数,它在跳跃点处不可导。这种更一般的情况可以通过测度论来统一描述,但超出了本课程的范围。
28. 示例:均匀分布 (Uniform Distribution)
均匀分布是最简单的概率分布之一,它表示在一个给定的区间内,所有事件发生的概率都是均等的。
-
离散均匀分布:
- 场景: 一个离散随机变量
在一个有限集合 中取值,且每个值被取到的概率完全相同。 - PMF:
。 - 特点: 重要的是状态的数量和它们的等可能性,状态的具体数值本身不影响概率分布。
- 场景: 一个离散随机变量
-
连续均匀分布:
- 场景: 一个连续随机变量
在一个区间 内取值,且在区间内任何位置的概率密度都相同。 - PDF:
- 特点: PDF 的图像是一个矩形,其高度为
,总面积为 。 - 计算概率: 计算
落入子区间 (其中 ) 的概率,就是计算对应矩形的面积:
- 场景: 一个连续随机变量
第六部分:概率论基本定理 (Basic Theorems of Probability)
有三条基本规则构成了概率论的运算基础,它们分别是加法法则、乘法法则和贝叶斯定理。
29. 加法法则 (Sum Rule) / 边缘化 (Marginalization)
加法法则建立了联合概率与边缘概率之间的关系。
-
核心思想: 如果我们知道两个或多个变量的联合分布,但只关心其中一个变量的分布,我们可以通过对其他不关心的变量进行求和(离散情况)或积分(连续情况)来“消除”它们的影响。这个过程被称为边缘化。
-
定义:
其中
是随机变量 的所有可能取值的集合。 -
多变量情况: 对于一个包含
个变量的联合分布 ,我们可以通过对所有其他变量进行边缘化来获得任意一个变量 的边缘分布。
30. 乘法法则 (Product Rule) / 链式法则
乘法法则描述了如何将一个联合概率分解为条件概率和边缘概率的乘积。
- 核心思想: 任何联合分布都可以被分解。这来自于条件概率的定义
。 - 定义:
- 对称性: 因为联合概率是对称的(即
),所以我们同样可以写成: - 推广 (链式法则): 对于多个变量,我们可以反复应用乘法法则,将其分解为一系列条件概率的乘积:
31. 贝叶斯定理 (Bayes' Theorem)
贝叶斯定理是概率论中最核心、最重要的定理之一,它为我们提供了一种在观测到新证据后,更新我们已有信念的数学框架。
-
核心思想: 它将乘法法则的两种形式结合起来,建立了一个从
推断 的桥梁。 -
推导:
从乘法法则我们知道。
两边同时除以,即可得到贝叶斯定理: -
术语:
- 后验概率 (Posterior): 在观测到证据 之后,我们对 的信念。这是我们通常最想知道的结果。 - 似然 (Likelihood): 假设 为真,我们观测到证据 的概率。它描述了我们的模型(由 参数化)如何产生数据 。 - 先验概率 (Prior): 在没有任何证据之前,我们对 的初始信念。 - 证据 (Evidence) / 边缘似然: 观测到证据 的总概率。它通过对所有可能的 进行边缘化得到: 。它的作用是作为归一化常数,确保后验概率的积分为1。
-
似然 vs. 概率:
- 重要区分:
是关于 的概率分布,但它被看作是关于 的似然函数。我们说“ 的似然”,而不是“ 的似然”。 - 贝叶斯统计的核心就是更新我们的认知:
Posterior ∝ Likelihood × Prior。
- 重要区分:
第七部分:随机变量的函数 (Functions of Random Variables)
32. 基本概念
- 定义: 如果
是一个随机变量,而 是一个函数,那么 也是一个随机变量。 - 分布: 新的随机变量
的概率分布,完全由 的分布和函数 的形式所决定。 - 离散情况下的计算:
要计算取某个特定值 的概率,我们需要找到所有能够通过函数 映射到 的原始 值,并将它们对应的概率相加。 - 示例:
。如果 可以取 -2 和 2,那么 的概率就是 。
33. 变换与参数
- 随机变量的分布通常由一些参数来描述(例如,均值、方差)。
- 当我们对一个随机变量进行函数变换
时,新变量 的分布参数(如均值和方差)通常会发生改变,并且它们与原变量 的参数之间的关系,依赖于函数 的具体形式。这些关系将在后续内容中探讨。
第八部分:摘要统计量与独立性 (Summary Statistics and Independence)
为了描述和概括一个概率分布的关键特性,我们通常使用一些摘要统计量 (summary statistics),其中最重要的是均值 (mean) 和 (协)方差 ((co)variance)。
34. 期望 (Expected Value)
- 核心思想: 期望是一个随机变量取值的“加权平均”,权重就是每个值对应的概率(或概率密度)。它代表了如果我们进行无穷多次实验,所有结果的平均值会收敛到的那个理论值。
- 定义: 对于一个随机变量
和一个函数 ,其函数值 的期望 定义为: - 连续情况:
- 离散情况:
是随机变量 的所有可能取值的集合。 - 连续情况:
- 别名: 期望也被称为均值 (mean)、平均值 (average) 或一阶矩 (first moment)。
- 线性性: 期望是一个线性算子。对于任意函数
和常数 :
35. 均值、中位数与众数
这些都是描述分布“中心趋势”的指标。
-
均值 (Mean):
- 定义: 均值就是一个随机变量自身的期望,即当
时的期望值: - 多维情况: 对于一个随机向量
,其均值(期望)是逐元素计算的,结果是一个向量:
- 定义: 均值就是一个随机变量自身的期望,即当
-
理论均值 vs. 经验均值:
- 期望/理论均值 (Expected Value): 基于已知的完整概率分布计算出的理论平均值。
- 样本/经验均值 (Sample/Empirical Mean): 基于一个有限的观测数据集计算出的算术平均值。它是对理论均值的一个估计。
-
中位数 (Median):
- 将所有数据排序后位于最中间的那个值。50%的数据小于它,50%的数据大于它。
- 对于连续变量,它是使 CDF 等于 0.5 的那个值。
-
众数 (Mode):
- 数据中出现频率最高的那个值。
- 对于连续变量,它是使 PDF 达到峰值的那个值。一个分布可能有多个众数。
36. 方差与协方差
这些是描述分布“离散程度”或“变量间关系”的指标。
-
方差 (Variance):
- 定义: 方差衡量了一个随机变量
的取值与其均值 的偏离程度的平方的期望。它描述了数据分布的“胖瘦”或“分散程度”。 - 计算公式: 利用期望的线性性,可以推导出更方便的计算公式:
- 标准差 (Standard Deviation): 方差的平方根,记为
。它的单位与原始变量相同。
- 定义: 方差衡量了一个随机变量
-
协方差 (Covariance):
- 定义: 协方差衡量了两个随机变量
和 协同变化的程度。它是两个变量各自的偏差乘积的期望。 - 计算公式:
- 解读:
- 正协方差: 当 X 大于其均值时,Y 也倾向于大于其均值(正相关趋势)。
- 负协方差: 当 X 大于其均值时,Y 倾向于小于其均值(负相关趋势)。
- 零协方差: 两个变量之间没有线性相关性(但可能存在非线性关系)。
- 注意: 变量与自身的协方差就是其方差:
。
- 定义: 协方差衡量了两个随机变量
37. 多维随机变量的协方差
当处理的对象是随机向量时,协方差的概念被推广为协方差矩阵。
-
互协方差矩阵 (Cross-Covariance Matrix):
- 定义: 对于两个随机向量
和 ,它们之间的互协方差矩阵是一个 的矩阵,定义为: - 计算公式:
- 注意这里的
是一个外积,结果是一个 的矩阵。
- 定义: 对于两个随机向量
-
协方差矩阵 (Covariance Matrix):
- 定义: 如果我们计算一个随机向量
与自身的协方差,得到的就是协方差矩阵,通常记为 或 。这是一个 的方阵。 - 计算公式:
- 结构与解读:
- 对角线元素: 是向量中每个分量自身的方差,描述了各个维度的离散程度。
- 非对角线元素: 是不同分量之间的协方差,描述了不同维度之间的线性相关性。
- 重要性质:
- 协方差矩阵总是对称的 (
)。 - 协方差矩阵总是半正定的 (
对所有 成立)。
- 协方差矩阵总是对称的 (
- 定义: 如果我们计算一个随机向量
38. 相关性 (Correlation)
协方差的值会受到变量本身尺度的影响,一个值为100的协方差不一定比值为1的协方差代表更强的关系。为了有一个标准化的、与尺度无关的度量,我们使用相关系数。
-
定义: 两个单变量随机变量
和 之间的皮尔逊相关系数 (Pearson correlation coefficient) 是将它们的协方差进行标准化的结果: -
性质:
- 相关系数的值被限制在 [-1, 1] 区间内。
- corr = +1: 完全正线性相关。
- corr = -1: 完全负线性相关。
- corr = 0: 没有线性相关性。
- 它只衡量线性关系,对于非线性关系(例如 U 形),相关系数可能接近于0。
-
相关矩阵 (Correlation Matrix):
- 一个随机向量的相关矩阵,就是将其协方差矩阵进行标准化的结果。
- 它的对角线元素全部为 1。
- 它等价于先将每个随机变量进行“标准化”(减去均值,再除以标准差),然后计算这些标准化后的变量的协方差矩阵。
39. 统计独立性 (Statistical Independence)
独立性是概率论中一个非常强大且核心的概念,它极大地简化了多变量概率分布的分析和计算。
-
定义: 两个随机变量
和 被称为统计独立的 (statistically independent),当且仅当它们的联合概率等于它们各自边缘概率的乘积。 -
直观解释: 知道其中一个变量的取值,对另一个变量的取值不提供任何信息。
-
独立性的推论:
如果和 独立,那么: - 条件概率等于边缘概率:
- 期望的乘积:
。 - 协方差为零:
。
- 方差的可加性:
。
- 条件概率等于边缘概率:
-
协方差为零 vs. 独立性:
- 独立
协方差为零: 这个方向总是成立的。 - 协方差为零
独立: 这个方向不一定成立!协方差为零只意味着两个变量之间没有线性关系,但它们之间可能存在复杂的非线性依赖关系。 - 示例: 设随机变量
的分布对称于0(例如标准正态分布),因此 且 。令 。显然 完全依赖于 。但它们的协方差是: 尽管协方差为零,但 和 显然不是独立的。
- 独立
40. 独立同分布 (Independent and Identically Distributed, i.i.d.)
在机器学习中,我们最常遇到的假设就是数据是独立同分布 (i.i.d.) 的。
对于一组随机变量
- 独立 (Independent): 变量之间是相互独立的。知道任何一个或多个变量的取值,都不会影响对其他变量取值的判断。
- 同分布 (Identically Distributed): 每一个随机变量
都服从完全相同的概率分布。
总结: i.i.d. 假设意味着,我们的每一个数据点都是从同一个未知的“数据生成器”中独立抽取出来的样本。这个假设是许多统计推断和机器学习算法的理论基础。
41. 条件独立性 (Conditional Independence)
这是一个比独立性更微妙、也更普遍的概念。
-
定义: 给定第三个随机变量
,我们称 和 在给定 的条件下是条件独立的,当且仅当: -
直观解释: 如果我们已经知道了
的信息,那么 的信息对于推断 就不再提供任何额外的新信息了。 -
等价形式:
-
示例:
- 设一个盒子里有一枚公平硬币 (C=fair) 和一枚两面都是正面的硬币 (C=biased)。
- 实验: 随机选一枚硬币,然后连续抛掷两次。
- 变量: A = 第一次是正面,B = 第二次是正面。
- 分析:
- 非独立的: 在不知道选的是哪枚硬币的情况下,如果观察到第一次是正面(事件A),那么我们更有可能选中的是那枚两面硬币,因此第二次也是正面的概率会变高。所以,A 和 B 不是无条件独立的。
- 条件独立的: 如果我们已经知道了我们选中的是公平硬币(给定 C=fair),那么第一次抛掷的结果对第二次就没有任何影响了,
。此时,A 和 B 在给定 C 的条件下是条件独立的。
- 许多复杂的概率模型(如图模型、贝叶斯网络)的核心就是利用条件独立性来简化变量之间的依赖关系。
第九部分:随机变量的和与变换 (Sums and Transformations of Random Variables)
本部分将总结一些关于期望和(协)方差的重要运算性质,特别是在处理随机变量的线性组合和仿射变换时。
42. 期望与方差的基本性质
-
符号约定:
- 均值/期望:
- 方差/协方差矩阵:
(即 )
- 均值/期望:
-
随机变量之和的性质:
对于两个随机向量: - 期望的和: 期望算子是线性的,总是成立。
- 方差的和:
- 重要特例: 如果
和 是不相关的(即 ),那么方差也具有可加性: 。独立性是协方差为零的更强条件。
- 重要特例: 如果
- 期望的和: 期望算子是线性的,总是成立。
43. 仿射变换 (Affine Transformation)
在机器学习中,我们经常对数据或参数进行线性变换,这是一个非常重要的场景。
-
问题设定:
- 设
是一个随机向量,其均值为 ,协方差矩阵为 。 - 我们对其进行一个仿射变换,得到一个新的随机向量
: 其中, 和 是确定的(非随机的)矩阵和向量。
- 设
-
变换后的均值:
利用期望的线性性质,我们可以直接得到的均值: - 结论: 对一个随机变量进行仿射变换,其均值也会进行完全相同的仿射变换。
-
变换后的协方差矩阵:
我们来计算的协方差矩阵: - 结论: 随机向量经过仿射变换
后,其新的协方差矩阵为 。注意,平移项 对协方差没有影响。
- 结论: 随机向量经过仿射变换
44. 互协方差的变换
- 问题: 考虑原随机向量
和变换后的随机向量 之间的互协方差 。 - 推导:
- 结论:
。
第十部分:高斯分布 (Gaussian Distribution)
高斯分布,也称为正态分布 (Normal Distribution),是概率论和统计学中最重要、研究最深入的连续概率分布。
45. 高斯分布的重要性
- 核心地位: 由于其优美的数学性质和广泛的适用性,高斯分布在机器学习中扮演着核心角色。
- 中心极限定理: 许多独立的随机过程,其总和的分布会趋向于高斯分布,这解释了它在自然界中的普遍性。
- 应用:
- 在线性回归中用作似然和先验。
- 作为高斯混合模型 (GMM) 的组件,用于密度估计。
- 在高斯过程 (Gaussian Processes)、变分推断 (Variational Inference)、强化学习、信号处理(如卡尔曼滤波器)和控制论(如线性二次调节器)中都是基础。
46. 高斯分布的数学形式
高斯分布完全由其均值和协方差矩阵这两个参数所决定。
-
单变量高斯分布 (Univariate Gaussian):
对于一个随机变量,其概率密度函数 (PDF) 为: 记为
。 -
多维高斯分布 (Multivariate Gaussian):
对于一个随机向量,其概率密度函数为: 记为
。 : 均值向量。 : 协方差矩阵。 : 协方差矩阵的行列式。 : 称为马氏距离 (Mahalanobis distance) 的平方,它衡量了点 到分布中心 的“统计距离”。
-
标准正态分布 (Standard Normal Distribution):
- 一个特殊情况,当均值为零向量 (
),协方差矩阵为单位矩阵 ( ) 时,称为标准正态分布,记为 。
- 一个特殊情况,当均值为零向量 (
47. 高斯分布的变换性质
高斯分布一个非常重要的特性是它在仿射变换下是封闭的 (closed),即一个高斯随机变量经过仿射变换后,其结果仍然服从高斯分布。
-
仿射变换:
- 设随机向量
。 - 我们对其进行仿射变换得到新的随机向量
。
- 设随机向量
-
变换后的分布:
仍然服从高斯分布,即 。 - 其新的均值和协方差矩阵可以直接通过我们之前推导的公式计算:
- 新均值:
- 新协方差:
- 新均值:
-
非线性变换:
- 如果对一个高斯随机变量进行非线性变换
,那么结果 通常不再服从高斯分布。 - 我们可以计算
的期望和方差,但这通常需要知道 的更高阶矩(例如,计算 需要积分)。 - 示例: 设
,其中 是高斯变量。 - 我们可以利用关系式
来求得 。 。 - 这两个值可以从原高斯分布的协方差矩阵(对角线元素)和均值向量中直接读出。
- 尽管我们可以计算出新变量的均值和方差,但它的完整分布形式通常是未知的或难以处理的。这在机器学习中引出了许多近似推断技术。
- 如果对一个高斯随机变量进行非线性变换